数学七年级下册2 等腰三角形教学设计

这是一份数学七年级下册2 等腰三角形教学设计，共3页。教案主要包含了课堂小结等内容，欢迎下载使用。
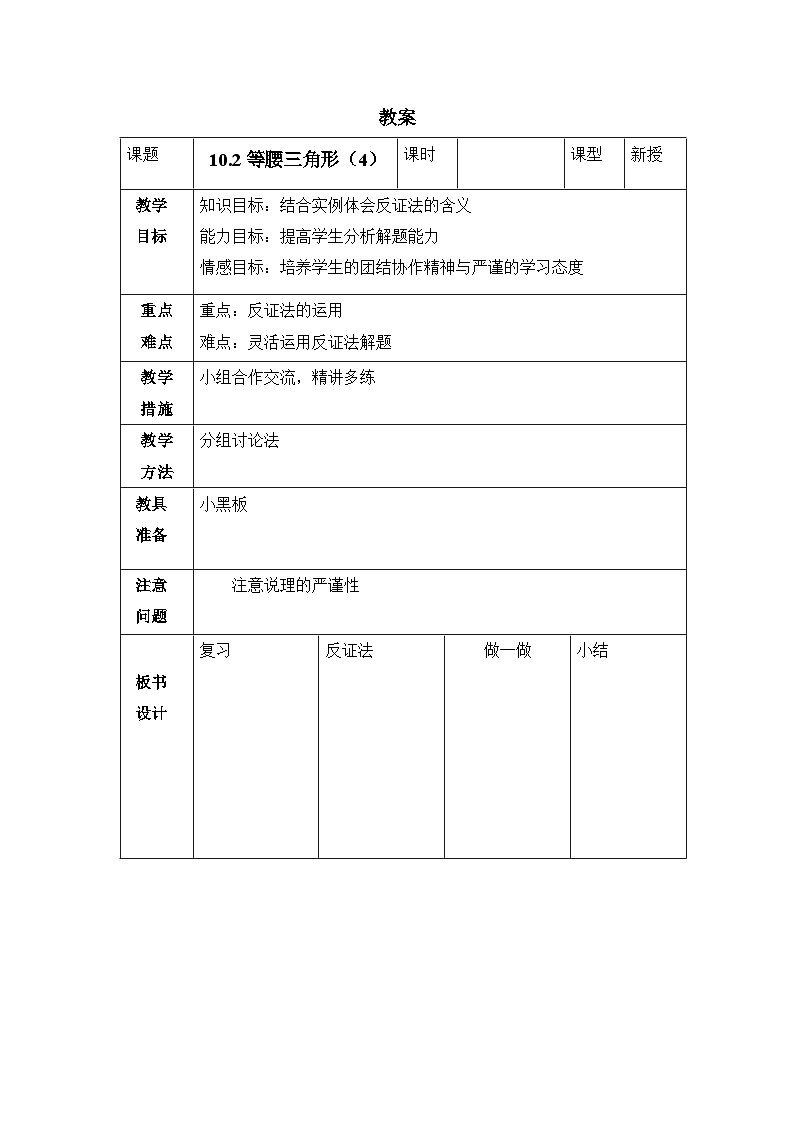
教案课题 10.2等腰三角形（4）课时 课型新授教学目标知识目标：结合实例体会反证法的含义能力目标：提高学生分析解题能力情感目标：培养学生的团结协作精神与严谨的学习态度重点难点重点：反证法的运用难点：灵活运用反证法解题教学措施小组合作交流，精讲多练教学方法分组讨论法 教具准备小黑板注意问题注意说理的严谨性 板书设计 复习反证法   做一做  小结    教 学 过 程  （包括导引新课、依标导学、异步训练、达标测试、作业设计等）复习：等边三角形的性质定理与判定定理是什么？直角在角形30度角所对的边与斜边有什么关系？想一想：小明说，在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等，你认为这个结论成立吗？如果成立，你能证明它吗？小明是这样想的：如果∠B≠∠C ，此时AB与AC要么相等，要么不等。假设AB＝AC，那么根据等边对等角，可知∠B＝∠C，但已知他们不等，这与已知矛盾，所以AB≠AC。反证法：先假设命题的结论不成立，然后推导出与定义、公理、已证定理或者已知条件相矛盾的结果，从而证明命题的结论一定成立，这种证明方法称为反证法。练一练：用反证法证明：一个三角形中至多有一个直角。已知，△ABC，求证∠B、∠C、∠A中至多有一个直角证明：假设∠B、∠C、∠A中有两个或三个直角，不妨设∠B＝∠A＝90度，则∠B+∠C+∠A＝90+90+∠C﹥180度。这与三角形内角和定理矛盾，所以∠B＝∠A＝90度不成立，所以一个三角形至多有一个直角。议一议
a1,a2,a3,a4,a5都是正数，且a1+a2+a3+a4+a5＝1，那么这五个数中至少有一个大于或等于1/5。  如何证明这一结论呢？假设这五个数中没有一个大于或者等于1/5，即都小于1/5，那么你能推出什么结论，这一结果与已知条件是否矛盾？   学生思考、讨论。练习：p109  随堂练习1、2      习题10.7  1、2四、课堂小结：学生总结本节内容。教 学 后 记（包括达标情况、教学得失、改进措施等）