初中数学湘教版七年级上册第3章 一元一次方程3.1 建立一元一次方程模型精品课件ppt

这是一份初中数学湘教版七年级上册第3章 一元一次方程3.1 建立一元一次方程模型精品课件ppt，共19页。PPT课件主要包含了已知数，未知数，这些等式都是方程，+03x5，25不是等内容，欢迎下载使用。
在小学算术中，我们学习了用算术方法解决实际问题的有关知识，那么，一个实际问题能否应用方程来解决呢？若能解决，怎样解？用方程解应用题与用算术方法解应用题相比较，它有什么优越性呢？
请你表示出下面两个问题中的等量关系.
（1）如图所示，甲、乙两站之间的高速铁路长1 068 km，“和谐号”高速列车从甲站开出2.5 h后，离乙站还有318 km. 该高速列车的平均速度是多少？
设高速列车的平均速度为x km/h，我们可以用含x的式子表示上述等量关系，即
2.5x + 318 = 1 068
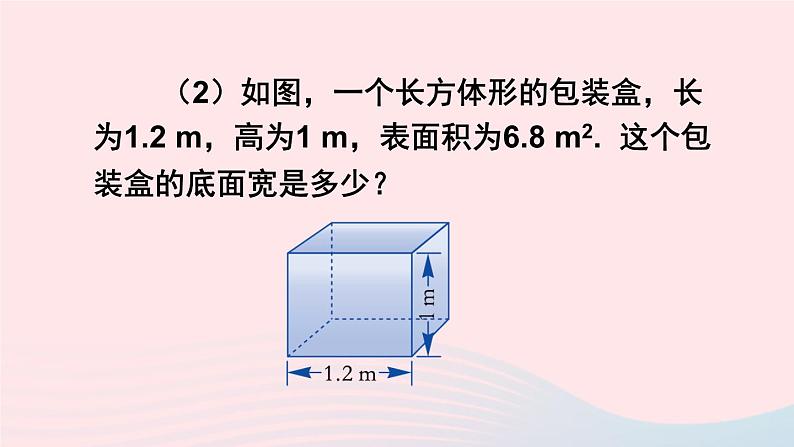
（2）如图，一个长方体形的包装盒，长为1.2 m，高为1 m，表面积为6.8 m2. 这个包装盒的底面宽是多少？
设包装盒的底面宽是y m，则等量关系可表示为
1.2×y×2+y×1×2+1.2×1×2 = 6.8，
即 2.4y + 2y + 2.4= 6.8
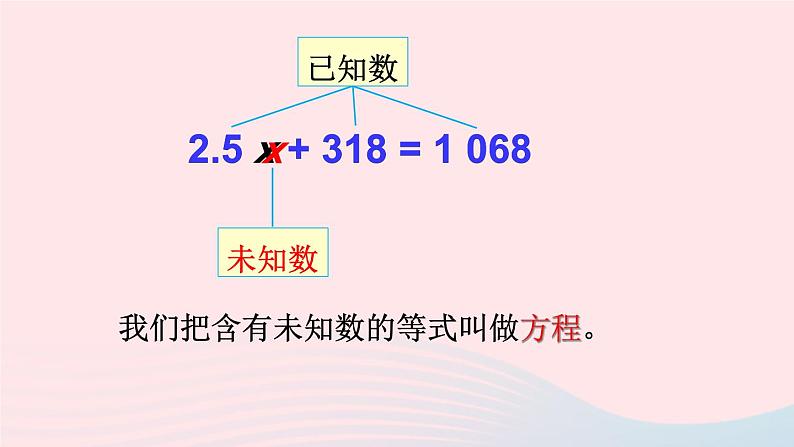
2.5 x + 318 = 1 068
2.5 + 318 = 1 068
我们把含有未知数的等式叫做方程。
2.4y + 2y + 2.4= 6.8
x – 2y = 6
一个未知数，次数是1。
我们把这样的方程叫做一元一次方程。
下面哪些方程是一元一次方程？
（1）3x + 4 = 5x – 1 （2）2x2 – x – 1 = 0（3）x – 2y=4 （4）3（2x – 7）=4（x – 5）
能使方程左、右两边相等的未知数的值，叫方程的解。
求方程的解的过程叫解方程.
检验下列x的值是否是方程2.5x+318=1 068的解。（1）x=300； （2）x=330.
解：（1）把x=300代入原方程得，左边=2.5×300+318=1 068，左边=右边，所以x=300是方程2.5x+318=1 068的解。
（2）把x=330代入原方程得，左边=2.5×330+318=1 143，左边≠右边，所以x=330不是方程2.5x+318=1 068的解。
1.奥运村奠基仪式上种了一棵树，刚移栽时，树高为2m，假设以后平均每年长0.3m，几年后树高为5m？设x年后树高为5m，可列出方程__________。
2.初一年级的女生占该年级学生数的52%，比该年级的男生多31人，初一年级共有多少学生？设初一年级共有学生x人，可列出方程_________________。
52%x – 48%x=31
3.判断下列方程是不是一元一次方程：
4.检验下列x的值是否是方程2x – 6 = 7x + 4的解。
（1）x = 2（2）x = – 2
解：（1）把x = 2代入原方程得，左边= 2×2 – 6 = – 2 ，右边=7×2+4=18，左边≠右边，所以x = 2不是方程2x – 6 = 7x + 4的解。
解：（2）把x = – 2代入原方程得，左边=2×（– 2） – 6 = – 10 ，右边=7×（– 2）+4 = – 10 ，左边=右边，所以x = – 2是方程2x – 6 = 7x + 4的解。