湖北省荆州市荆州区2022-2023学年八年级下学期期末数学试题

这是一份湖北省荆州市荆州区2022-2023学年八年级下学期期末数学试题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
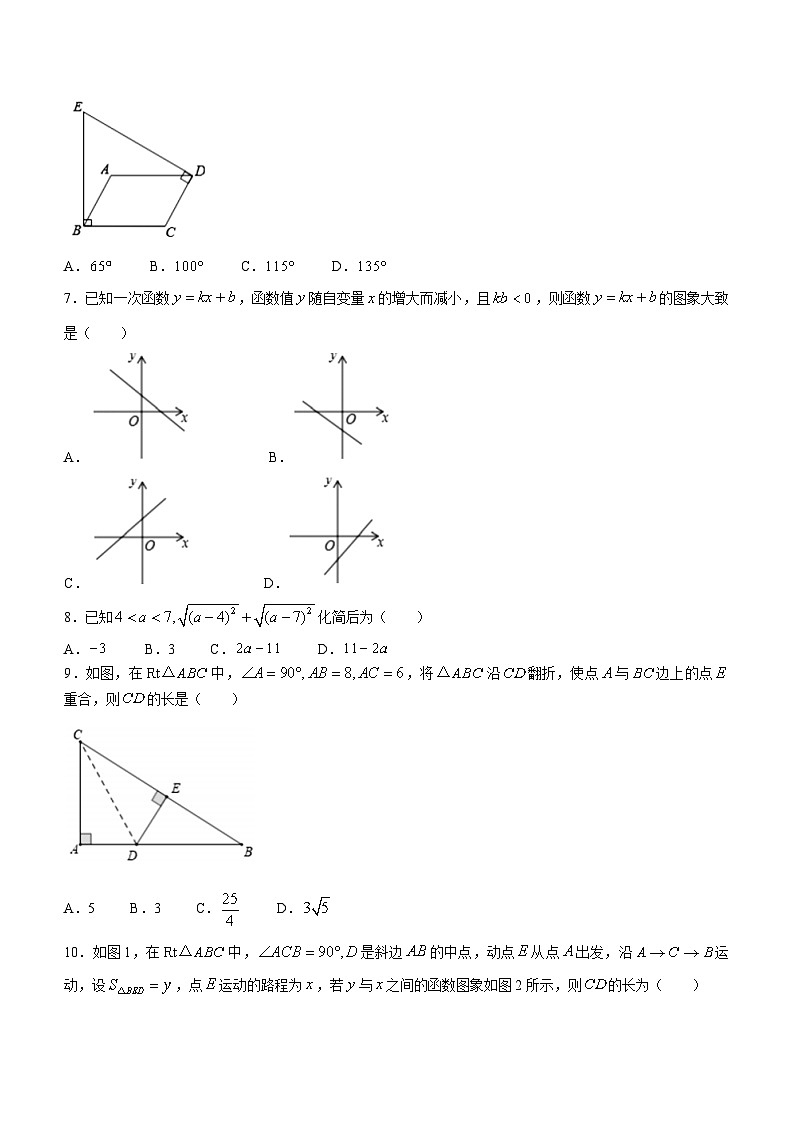
荆州区2022-2023学年度第二学期学业水平评价八年级数学试题（满分120分，考试时间120分钟）一、选择题（本大题共10小题，每小题3分，共30分）1．下列二次根式中，不能与合并的是（    ）A．     B．     C．     D．2．在函数中，自变量的取值范围是（    ）A．     B．     C．     D．3．下列计算正确的是（    ）A．                    B．C．     D．4．为了解某社区居民的用电情况，随机对该社区10户居民进行了调查，下表是这10户居民2021年4月份用电量的调查结果：居民（户）1324月用电量（度/户）40505560那么关于这10户居民用电量（单位：度），下列说法错误的是（    ）A．中位数是55     B．众数是60C．方差是29     D．平均数是545．下列命题错误的是（    ）A．顺次连接四边形各边中点得到的是矩形，则该四边形的对角线相互垂直B．对角线互相垂直平分的四边形为菱形C．直角三角形的两直角边长是3和4，则斜边长是5D．对角线垂直且相等的四边形是正方形6．如图，为平行四边形外一点，且，若，则的度数为（    ）A．     B．     C．     D．7．已知一次函数，函数值随自变量的增大而减小，且，则函数的图象大致是（    ）A．          B．C．          D．8．已知化简后为（    ）A．     B．3     C．     D．9．如图，在中，，将沿翻折，使点与边上的点重合，则的长是（    ）A．5     B．3     C．     D．10．如图1，在中，是斜边的中点，动点从点出发，沿运动，设，点运动的路程为，若与之间的函数图象如图2所示，则的长为（    ）          图1                              图2A．1     B．     C．2     D．4二、填空题（本大题共6小题，每小题3分，共18分）11．________．12．已知一组数据：3，3，4，5，5，则它的方差为________．13．如图，在中，点分别是的中点，连接，若，则________．14．如图，在平行四边形中，按以下步骤作图：①以为圆心，任意长为半径作弧，分别交于点；②分别以为圆心，以大于的长为半径作弧，两弧相交于点；③作射线，交边于点，若，则平行四边形周长为________．在15．同一平面直角坐标系中，一次函数与正比例函数的图象如图所示，则满足不等式的的取值范围是________．16．如图，在直角坐标系中，过点分别向轴、轴作垂线，垂足分别为点，取的中点，连结，作点关于直线的对称点，直线与交于点，交轴于点，则________．三、解答题（本大题共8小题，共72分）17．（8分）计算：（1）．（2）18．（8分）若，求的值．19．（8分）如图，在平行四边形中，为边上一点，平分，连接，若，．（1）求的长；（2）求平行四边形的面积；20．（8分）随着移动计算技术和无线网络的快速发展，移动学习方式越来越引起人们的关注．某校计划将这种学习方式应用到教育教学中，从各年级共1500名学生中随机抽取了部分学生，对其家庭中拥有的移动设备情况进行了调查，并绘制出如下的统计图①和图②，根据相关信息，解答下列问题：（1）本次接受随机抽样调查的学生人数为________人，图①中m的值为________；（2）本次调查获取的样本数据的众数是________台、中位数是________台、平均数是________台；（3）根据样本数据，估计该校学生家庭中拥有3台移动设备的学生人数．21．（8分）如图，在四边形中，是的中点，于点．（1）求证：四边形是菱形；（2）若，求的长．22．（10分）定义：对于给定的两个函数，任取自变量的一个值，当时，它们对应的函数值互为相反数；当时，它们对应的函数值相等，我们把这样的两个函数称作互为友好函数，例如：一次函数，它的友好函数为．（1）直接写出一次函数的友好函数．（2）已知点在一次函数的友好函数的图象上，求的值．（3）已知点在一次函数的友好函数的图象上，求的值．23．（10分）习近平总书记对实施乡村振兴战略作出重要指示强调：实施乡村振兴战略，是党的十九大作出的重大决策部署，是新时代做好“三农”工作的总抓手，为了发展乡村经济，某经销商计划购进A、B两种农产品．已知购进A种农产品2件，B种农产品3件，共需690元；购进A种农产品1件，B种农产品4件，共需720元．（1）A、B两种农产品每件的价格分别是多少元？（2）该经销商计划用不超过5400元购进A、B两种农产品共40件，且A种农产品的件数不超过B种农产品件数的3倍．如果该经销商将购进的农产品按照A种每件160元，B种每件200元的价格全部售出，那么购进A、B两种农产品各多少件时获利最多？24．（12分）如图，在平面直角坐标系中，矩形的顶点在轴的正半轴上，点在轴的正半轴上，线段的长分别是且满足，点是线段上一点，将沿直线翻折，点落在矩形对角线上的点处．（1）求线段的长；（2）求点的坐标；（3）若所在直线与相交于点，点在轴的正半轴上，以为顶点的四边形是平行四边形时，求点坐标．荆州区2022-2023学年度第二学期学业水平评价八年级数学参芳答案一、选择题1．C  2．D  3．C  4．C  5．D  6．C  7．A  8．B  9．D  10．B二、填空题11．  12．  13．8  14．20  15．  16．10三\\解答题17．（1）（2）原式．18．，．．19．（1）四边形是平行四边形，，，平分，，；（2）四边形是平行四边形．，在中，，，．，平行四边形的面积为．20．（1）50，32；（2）众数为4；中位数是3；平均数是3.2．（3）（人）．答：估计该校学生家庭中；拥有3台移动设备的学生人数约为420人．21．（1）证明：，四边形是平行四边形，是的中点，，四边形是菱形；（2）解：过作于点，如图所示，，的面积，，点是的中点，四边形是菱形，，，．22．（1）的友好函数为，（2）因为，所以把代入中得，；（3）当时，把代入中得，；当时，把代入中得，，．23．（1）设每件进价元，每件进价元，由题意得，解得：，答：每件进价120元，每件进价150元；（2）设农产品进件，农产品件，由题意得，解得，设利润为元，则，随的增大而减小，当时，最大，最大值，答：农产品进20件，农产品进20件，最大利润是1800元．24．（1）∵线段的长分别是且满足；设，由翻折的性质可得：，，可得：，在中，由勾股定理可得：，即，解得：，可得：，（2）过作，在中，，即解得：，在中，，，所以点的坐标为，（3）设直线的解析式为：，把代入解析式可得：，解得：，所以的解析式为：，把代入的解析式，可得：，即，当以为顶点的四边形是平行四边形时，，所以，即存在点，且点的坐标为或．