人教版九年级上册22.3 实际问题与二次函数教学课件ppt

这是一份人教版九年级上册22.3 实际问题与二次函数教学课件ppt，共14页。PPT课件主要包含了新课导入，教学设计，探究新知，知识归纳，例题与练习，随堂练习，解得a，课堂小结等内容，欢迎下载使用。

现实生活中你一定见过各式各样的抛物线形拱桥(如图)吧？能不能利用二次函数的知识解决与之相关的问题呢？
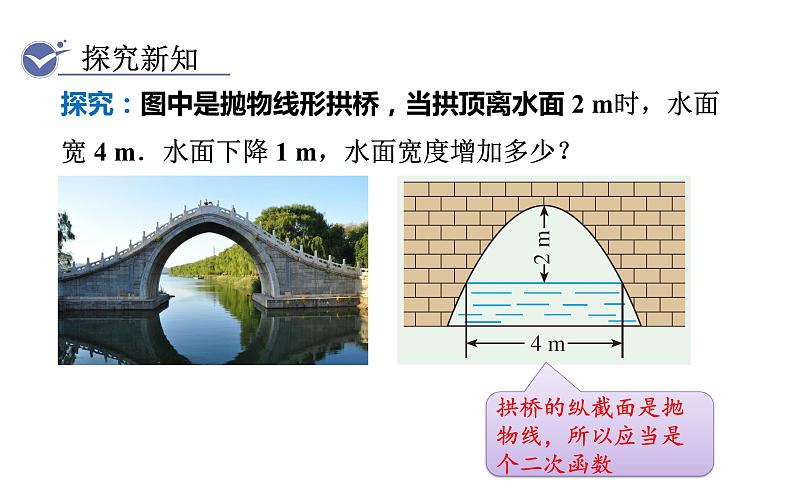
探究：图中是抛物线形拱桥，当拱顶离水面 2 m时，水面宽 4 m．水面下降 1 m，水面宽度增加多少？
拱桥的纵截面是抛物线，所以应当是个二次函数
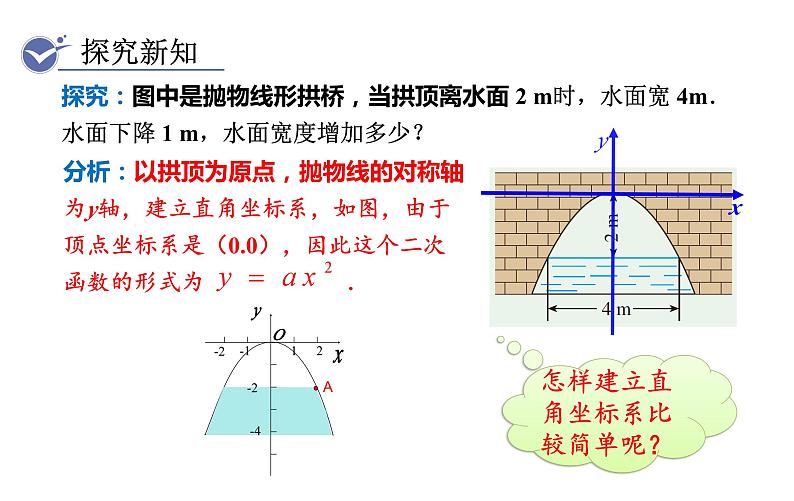
探究：图中是抛物线形拱桥，当拱顶离水面 2 m时，水面宽 4m．水面下降 1 m，水面宽度增加多少？
怎样建立直角坐标系比较简单呢？
分析：以拱顶为原点，抛物线的对称轴为y轴，建立直角坐标系，如图，由于顶点坐标系是（0.0），因此这个二次函数的形式为 ．
解：设这条抛物线表示的二次函数为y＝ax2.由抛物线经过点(2，－2)，可得－2＝a×22，a＝－这条抛物线表示的二次函数为y＝－ x2.当水面下降1 m时，水面的纵坐标为－3.当 y = -3时，- x2= -3，解得 x1= ，x2= - ，所以当水面下降1 m时，水面宽度为 m.水面下降1 m，水面宽度增加________m.
你还有其他的解决方法吗？
1．将线段长度转化为点的坐标问题．2．利用点的坐标以及抛物线的特点，设出函数解析式并求解．3．利用函数解析式求点的坐标，转化为线段的长度．
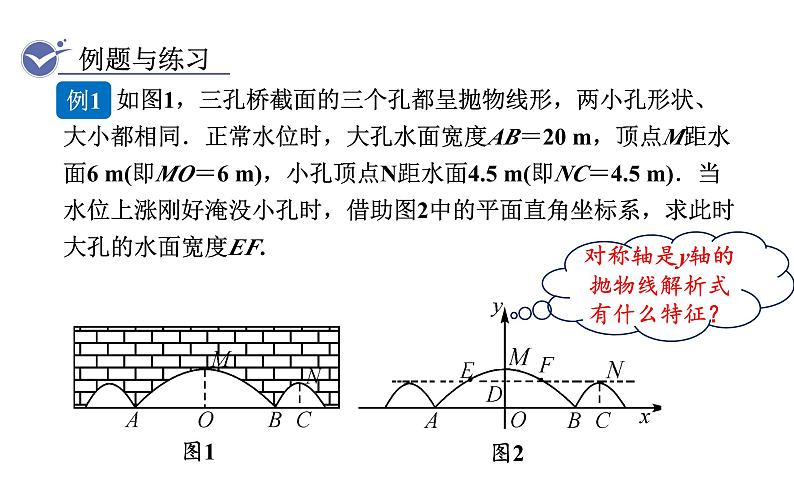
如图1，三孔桥截面的三个孔都呈抛物线形，两小孔形状、大小都相同．正常水位时，大孔水面宽度AB＝20 m，顶点M距水面6 m(即MO＝6 m)，小孔顶点N距水面4.5 m(即NC＝4.5 m)．当水位上涨刚好淹没小孔时，借助图2中的平面直角坐标系，求此时大孔的水面宽度EF.
对称轴是y轴的抛物线解析式有什么特征？
解：设大孔对应的抛物线的函数解析式为y＝ax2＋6.
依题意，得B(10，0)，
解得a＝－0.06，即y＝－0.06x2＋6.
当y＝4.5时，－0.06x2＋6＝4.5，解得x＝±5.
∴DE＝DF＝5 m，
∴a×102＋6＝0，
∴EF＝10 m，即水面宽度EF为10 m.
如图，小明的父亲在相距2 m的两棵树间拴了一根绳子，给他做了一个简易的秋千，拴绳子的地方A，B距地面高都是2.5 m，绳子自然下垂呈抛物线状，身高1 m的小明距较近的那棵树0.5 m时，头部刚好接触到绳子C处，求绳子的最低点距地面的距离为多少米？
解：根据如图所示的平面直角坐标系，可设它的函数解析式为y＝ax2＋k.
把B(1，2.5)，C(－0.5，1)代入，可求得a＝2，k＝0.5，
∴抛物线的解析式为y＝2x2＋0.5.
∵a＝2＞0，∴y有最小值，
∴当x＝0时，y最小＝0.5.
答：绳子的最低点距地面的距离为0.5 m.
1．欢欢在今年的校运会跳远比赛中跳出了满意的一跳，函数h＝3.5t－4.9t2(t的单位：s，h的单位：m)可以描述她跳跃时重心高度随时间的变化关系，则她起跳后到重心到达最高时所用的时间是 s.
2．某学校九年级的一场篮球比赛中，如图，队员甲正在投篮，已知球出手时离地面高 m，与篮圈中心的水平距离为7 m，当球出手后水平距离为4 m时到达最大高度4 m，设篮球运行轨迹为抛物线，篮圈距地面3 m. (1)建立如图所示的平面直角坐标系，问此球能否准确投中？(2)此时，若对方队员乙在甲面前1m处跳起盖帽拦截，已知乙的最大摸高为3.1 m，则他能否获得成功？
解：（1）由题意可知，抛物线经过点（0， ），顶点坐标是（4，4），篮圈中心的坐标是（7，3）．
设抛物线的解析式是y=a（x-4）2+4，
∴ =16a+4
∴抛物线解析式为y= （x-4）2+4．
当x=7时，y= ×（7-4）2+4=3，
∴篮圈的中心点在抛物线上，
（2）∵当x=1时，y= ×（1-4）2+4=3＜3.1，
解决抛物线型建筑问题的步骤：
注意：同一个问题中，建立平面直角坐标系的方法有多种，建立适当的平面直角坐标系能简化函数解析式.通常应使已知点在坐标轴上。
(1)建立适当的平面直角坐标系，将抛物线形的图形放在坐标系中；
(2)设出函数解析式，结合图形和已知条件，用待定系数法求函数解析式；
(3)利用二次函数的图象与性质求解实际问题.