高中数学湘教版（2019）选择性必修 第一册3.1 椭圆说课课件ppt

这是一份高中数学湘教版（2019）选择性必修 第一册3.1 椭圆说课课件ppt，共39页。PPT课件主要包含了目录索引等内容，欢迎下载使用。
1.理解椭圆的定义及椭圆的标准方程;2.掌握用定义法和待定系数法求椭圆的标准方程;3.理解椭圆标准方程的推导过程,并能运用标准方程解决相关问题.
基础落实·必备知识全过关
重难探究·能力素养全提升
学以致用·随堂检测全达标
平面上到两个定点F1,F2的距离之　　为常数(大于　　　　)的点的轨迹叫作椭圆.这两个定点F1,F2叫作椭圆的　　　　,两个焦点之间的距离|F1F2|叫作　　　　. 名师点睛椭圆的定义用集合语言叙述为:{P||PF1|+|PF2|=2a,2a>|F1F2|}.
所有满足条件的点的集合
过关自诊1.判断正误.(正确的画√,错误的画×)(1)平面上到两个定点F1,F2的距离之和等于常数的点的集合是椭圆.(　　)(2)椭圆的特殊形式是圆.(　　)2.将椭圆定义中“大于|F1F2|”改为“等于|F1F2|”,其他条件不变,点的轨迹是什么?改为“小于|F1F2|”呢?
提示当距离之和等于|F1F2|时,点的轨迹是线段F1F2.当距离之和小于|F1F2|时,动点的轨迹不存在.
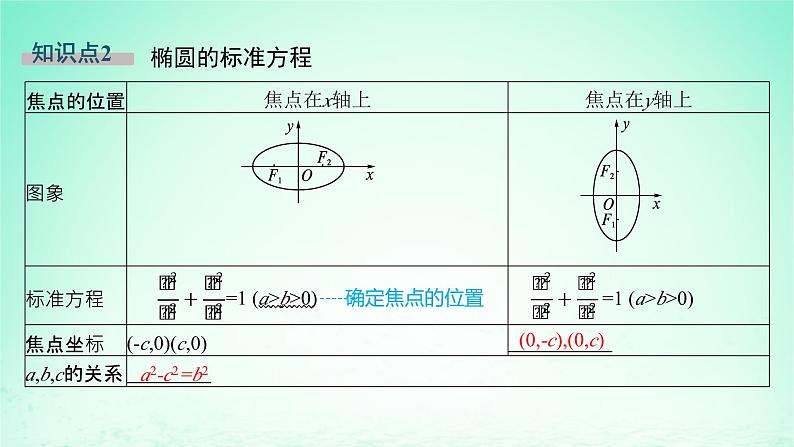
(0,-c),(0,c)
名师点睛1.若椭圆的焦点在x轴上,则标准方程中x2项的分母较大;若椭圆的焦点在y轴上,则标准方程中y2项的分母较大.简记为:焦点位置看大小,焦点跟着大的跑.2.点与椭圆的位置关系:
过关自诊1.判断正误.(正确的画√,错误的画×)(1)椭圆x2+ =1与椭圆y2+ =1虽然焦点坐标不同,但是焦距相同.(　　)(2)若ab>0,则方程ax2+by2=1是椭圆的方程.(　　)2.在椭圆的标准方程中,a>b>c一定成立吗?
提示不一定,只需a>b,a>c即可,b,c的大小关系不确定.
探究点一 求椭圆的标准方程
角度1待定系数法【例1】求适合下列条件的椭圆的标准方程:
分析(1)可以利用焦点坐标求c,利用定义求a;(2)由于焦点位置已知,因此可以直接设出方程,将点的坐标代入求解;(3)由于焦点不确定,因此可以设方程为mx2+ny2=1(m>0,n>0,m≠n),列式求解.
规律方法　待定系数法求椭圆标准方程的步骤
变式训练1求适合下列条件的椭圆的标准方程:(1)a+c=10,a-c=4;(2)焦点在x轴上,焦距为4,且椭圆过点(0,2);(3)经过(-2,0),( ,-1)两点.
解 (1)∵a+c=10,a-c=4,∴a=7,c=3,∴b2=a2-c2=72-32=40.
角度2定义法【例2】一个动圆与圆Q1:(x+3)2+y2=1外切,与圆Q2:(x-3)2+y2=81内切,试求这个动圆圆心的轨迹方程.分析 设出动圆的圆心及半径,利用两圆相切的几何条件列式求解.
解 两定圆的圆心和半径分别为Q1(-3,0),r1=1;Q2(3,0),r2=9.设动圆圆心为M(x,y),半径为R,由题意有|MQ1|=1+R,|MQ2|=9-R,∴|MQ1|+|MQ2|=10>|Q1Q2|=6.由椭圆的定义可知点M在以Q1,Q2为焦点的椭圆上,且a=5,c=3,∴b2=a2-c2=25-9=16.
变式探究本例题两个已知圆不变,若动圆与两个圆都内切,求动圆圆心的轨迹方程.
解 设动圆圆心为P(x,y),半径为r.由圆P与圆Q1内切,得|PQ1|=r-1;由圆P与圆Q2内切,得|PQ2|=9-r.所以|PQ1|+|PQ2|=8>6=|Q1Q2|.所以点P轨迹是以Q 1,Q 2为焦点的椭圆,且2a=8,2c=6.即a=4,c=3,所以b2=a2-c2=7.
规律方法　定义法求椭圆标准方程的方法若动点的轨迹满足椭圆的定义,可直接根据定义求椭圆的方程.其一般步骤为:(1)将条件转化为到两定点的距离之和为定值(该定值大于两定点之间的距离);(2)确定椭圆的基本量a,b,c,从而确定椭圆的标准方程.
变式训练2若动圆M过定点A(-3,0),且内切于定圆B:(x-3)2+y2=100,则动圆圆心M的轨迹方程为　　　　　　　　. 
解析 圆B的圆心为B(3,0),半径为r1=10.∵(-3-3)2+02=36|AB|.∴动圆圆心M的轨迹是以A,B为焦点的椭圆,此时a=5,c=3,∴b2=a2-c2=16.
探究点二 对椭圆标准方程的理解
【例3】(1)若方程 =1表示椭圆,则实数m的取值范围是(　　)A.(-9,25)B.(-9,8)∪(8,25)C.(8,25)D.(8,+∞)
即实数m的取值范围是(-9,8)∪(8,25).
(2)若方程x2-3my2=1表示焦点在x轴上的椭圆,则实数m的取值范围是　　　　　　　　　. 
规律方法　根据椭圆的方程求参数取值范围的方法
变式训练3若方程 =1表示焦点在x轴上的椭圆,则实数a的取值范围是(　　)A.(3,+∞)B.(-∞,-2)C.(-∞,-2)∪(3,+∞)D.(-6,-2)∪(3,+∞)
解析 因为椭圆的焦点在x轴上,
解得a>3或-6