新教材2023_2024学年高中数学第4章计数原理培优课两个原理的应用课件湘教版选择性必修第一册

这是一份新教材2023_2024学年高中数学第4章计数原理培优课两个原理的应用课件湘教版选择性必修第一册，共21页。

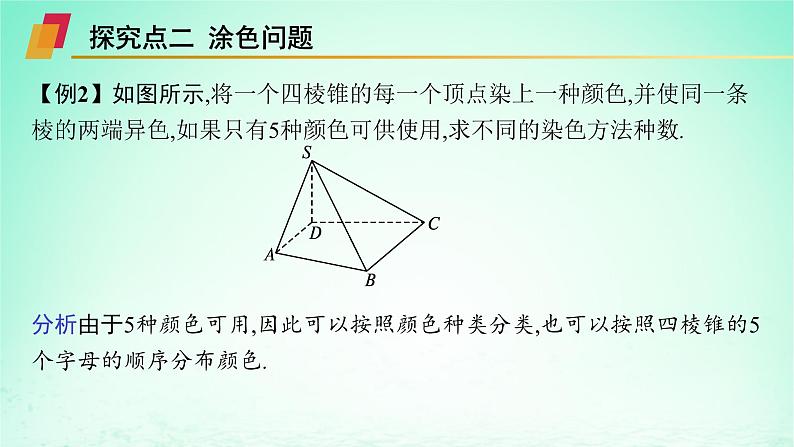
第4章培优课　两个原理的应用重难探究·能力素养全提升目录索引 学以致用·随堂检测全达标重难探究·能力素养全提升探究点一 组数问题【例1】用0,1,2,3,4五个数字,(1)可以组成多少个三位数的电话号码?(2)可以组成多少个三位数?(3)可以组成多少个能被2整除的无重复数字的三位数?分析 根据所组数字的特征,利用两个原理求解.解 (1)三位数字的电话号码,百位上的数字可以是0,数字也可以重复,每个位置上的数字都有5种取法,根据分步乘法计数原理,可以组成5×5×5=125个三位数字的电话号码.(2)三位数的百位上的数字不能为0,但可以有重复数字,首先考虑百位上的数字的取法,除0外共有4种取法,个位、十位上的数字可以取0,根据分步乘法计数原理,可以组成4×5×5=100个三位数.(3)被2整除的数即偶数,个位数字可取0,2,4,因此,可以分两类,一类是个位数字是0,可以组成4×3=12个无重复数字的三位数;一类是个位数字不是0,则个位上的数字有2种取法,即2或4,再考虑百位上的数字,因为0不能是百位上的数字,所以有3种取法,十位有3种取法,因此有2×3×3=18个无重复数字的三位数.因而有12+18=30(个)三位数,即可以组成30个能被2整除的无重复数字的三位数.变式探究由本例中的五个数字可组成多少个无重复数字的四位奇数?解 完成“组成无重复数字的四位奇数”这件事,可以分四步:第1步,定个位,只能从1,3中任取一个,有2种方法;第2步,定千位,把1,2,3,4中除去用过的一个数,在剩下的3个数中任取一个,有3种方法;第3步,把剩下的包括0在内的3个数字先排百位,有3种方法;第4步,排十位,有2种方法.由分步乘法计数原理知,共能组成2×3×3×2=36个无重复数字的四位奇数.规律方法　利用两个原理求解数字组数问题的方法(1)明确特殊位置或特殊数字,是我们采用“分类”还是“分步”的关键.一般按特殊位置(或特殊元素)分类,分类中再按特殊位置(或特殊元素)优先的策略分步完成;如果正面分类较多,可采用间接法求解.(2)要注意数字“0”不能排在两位数或两位以上的数字的最高位.探究点二 涂色问题【例2】如图所示,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱的两端异色,如果只有5种颜色可供使用,求不同的染色方法种数.分析由于5种颜色可用,因此可以按照颜色种类分类,也可以按照四棱锥的5个字母的顺序分布颜色.解 (方法1　先分步再分类)　按S,A,B,C,D的顺序分步染色:第一步,S点染色,有5种方法;第二步,A点染色,与S在同一条棱上,有4种方法;第三步,B点染色,与S,A分别在同一条棱上,有3种方法;第四步,C点染色,但考虑到D点与S,A,C分别在同一条棱上,需要针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法;当A与C不同色时,因为C与S,B也不同色,所以C点有2种染色方法,D点也有2种染色方法.由分步乘法计数原理、分类加法计数原理,得不同的染色方法种数为5×4×3×(3×1+2×2)=420.(方法2　先分类再分步)　按所用颜色种类分类:第一类,5种颜色全用,共有5×4×3×2×1=120种不同的方法;第二类,只有4种颜色,则必有某两个顶点同色(A与C或B与D),共有2×5×4×3×2=240种不同的方法;第三类,只有3种颜色,则A与C,B与D必定同色,共有5×4×3=60种不同的方法.由分类加法计数原理,得不同的染色方法种数为120+240+60=420.规律方法　求解涂色问题一般常用方法涂色问题一般是综合利用两个计数原理求解,有几种常用方法:(1)按区域的不同,以区域为主分步计数,用分步乘法计数原理分析.(2)以颜色为主分类讨论,适用于“区域、点、线段”等问题,用分类加法计数原理分析.(3)将空间问题平面化,转化为平面区域的涂色问题.种植问题按种植的顺序分步进行,用分步乘法计数原理计数或按种植品种恰当选取情况分类,用分类加法计数原理计数.变式训练一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为n(n≥3,n∈N+)等份,种植红、黄、蓝三种颜色不同的花,要求相邻两部分种植不同颜色的花.(1)如图1,圆环分成3等份,分别为a1,a2,a3,则有多少种不同的种植方法?(2)如图2,圆环分成4等份,分别为a1,a2,a3,a4,则有多少种不同的种植方法?解 (1)分两步.第一步,先种植a1部分,有3种不同的种植方法;第二步,再种植a2,a3部分.因为a2,a3与a1的颜色不同,a2,a3的颜色也不同,则a2有2种不同的种植方法,a3有1种不同的种植方法.由分步乘法计数原理,不同的种植方法有3×2×1=6种.(2)分两类.第一类,当a1,a3不同色时,有3×2×1×1=6种种植方法;第二类,当a1,a3同色时,有3×2×1×2=12种种植方法.由分类加法计数原理得,共有6+12=18种种植方法.学以致用·随堂检测全达标123451.从0,1,2,3,4,5这六个数字中,任取两个不同数字相加,其和为偶数的不同取法的种数有(　　)A.30种 B.20种 C.10种 D.6种D解析 从0,1,2,3,4,5这六个数字中,任取两个不同数字相加和为偶数可分为两类.第一类,取出的两数都是偶数,共有3种取法;第二类,取出的两数都是奇数,共有3种取法.由分类加法计数原理得,共有N=3+3=6种不同取法.故选D.123452.由2,3,5,0组成的没有重复数字的三位偶数的个数是　　　　,三位奇数的个数是　　　　. 108解析 数按照末位数字分两类进行:第一类,个位是0时,百位有3种选法,十位有2种选法,共有3×2=6个没有重复数字的偶数;第二类,当末位是2时,百位只能从3,5中选1个,有2种选法;十位有2种选法,共有2×2=4个没有重复数字的偶数.由分类加法计数原理可知,共有6+4=10个没有重复数字的三位偶数.奇数的末位数可以从3,5中选1个,首位从3,5中剩余的一个与2中选1个,有2种方法,同理第二位也有2种方法,由分步乘法计数原理可知,共有2×2×2=8个没有重复数字的三位奇数.13453.如图,用2种不同的颜色涂所给图形中的四个区域,要求相邻区域的颜色不能相同,则不同的涂色方法有　　　　种. 2213454. 如图所示,在某高中校园内有一个标志性图标,该图标是由一个圆、一个三角形和一个长方形构成,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个图形颜色不全相同的情形有　　　　种. 2613452解析 个圆、一个三角形和一个长方形分别涂红色或蓝色,所有可能出现的结果如下: 所以三个图形颜色不全相同的情形有6种. 13455. 用红、黄、蓝、绿4种颜色给图中的A,B,C三个区域涂色,要求每个区域只能涂一种颜色.(1)颜色不能重复使用,有多少种不同的涂色方法?(2)相邻区域不能涂同一种颜色,有多少种不同的涂色方法?2解 (1)依题意,分3步进行:第一步,考虑A区域,有4种颜色可选择;第二步,考虑B区域,不能选A区域的颜色,有3种颜色可选择;第三步,考虑C区域,不能选A,B区域的颜色,有2种颜色可选择.根据分步乘法计数原理知,有4×3×2=24种不同的涂色方法.13452(2)依题意,分3步进行:第一步,考虑A区域,有4种颜色可选择;第二步,考虑B区域,不能选A区域的颜色,有3种颜色可选择;第三步,考虑C区域,不能选B区域的颜色,有3种颜色可选择.根据分步乘法计数原理知,有4×3×3=36种不同的涂色方法.