高中数学湘教版（2019）选择性必修第一册2.6 直线与圆、圆与圆的位置关系备课ppt课件

展开

这是一份高中数学湘教版（2019）选择性必修第一册2.6 直线与圆、圆与圆的位置关系备课ppt课件，共36页。PPT课件主要包含了目录索引等内容，欢迎下载使用。

1.理解并掌握圆与圆的位置关系及判断方法;2.掌握圆与圆的位置关系的代数判断方法与几何判断方法,能够利用上述方法判断两圆的位置关系.
基础落实·必备知识全过关
重难探究·能力素养全提升
学以致用·随堂检测全达标
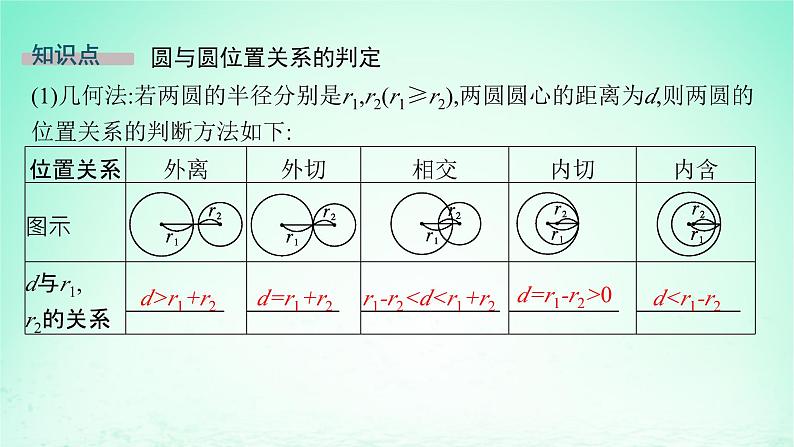
(1)几何法:若两圆的半径分别是r1,r2(r1≥r2),两圆圆心的距离为d,则两圆的位置关系的判断方法如下:
r1-r2d=r1-r2>0　
(3)拓展知识:圆系方程常见圆系方程有如下几种:1.过直线与圆的交点的圆系:过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0;特别地,当直线与圆相切于点P时,上述方程表示与直线和圆都相切于点P的圆.2.过两个圆的交点的圆系:过两圆x2+y2+D1x+E1y+F1=0,x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1),此圆系不含圆x2+y2+D2x+E2y+F2=0.
3.同心圆系:与圆x2+y2+Dx+Ey+F=0同心的圆系方程为x2+y2+Dx+Ey+λ=0;或表示为与已知圆(x-a)2+(y-b)2=r2同心的圆系方程为(x-a)2+(y-b)2=R2(其中a,b为定值).
名师点睛1.当两圆外离时公切线的条数是4条,外切时公切线的条数是3条,相交时公切线的条数是2条,内切时公切线的条数是1条,内含时两圆不存在公切线.2.当两圆相交时,两圆圆心的连线垂直平分公共弦;当两圆外切时,两圆圆心的连线垂直于过两圆公共点的公切线;当两圆内切时,两圆圆心的连线垂直于两圆的公切线.3.对圆系方程可进行以下推广:对过两已知圆交点的圆系方程,当λ=-1时,得到(D1-D2)x+(E1-E2)y+F1-F2=0,此为两圆公共弦所在直线方程.
过关自诊1.判断正误.(正确的画√,错误的画×)(1)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.(　　)(2)将两圆的方程组成方程组消元后,得到的一元二次方程.若方程无解,则两圆外离.(　　)(3)如果两圆的圆心距小于两圆的半径之和,则两圆相交.(　　)
2.思考:将两个相交的非同心圆的方程x2+y2+Dix+Eiy+Fi=0(i=1,2)相减,可得一直线方程,这条直线方程具有什么样的特殊性呢?
提示两圆相减得一直线方程,该直线经过两圆的公共点.经过相交两圆的公共交点的直线是两圆的公共弦所在的直线.
探究点一圆与圆的位置关系的判断
【例1】已知圆C1:x2+y2-2ax-2y+a2-15=0(a>0),圆C2:x2+y2-4ax-2y+4a2=0(a>0).试求a为何值时,两圆C1,C2的位置关系满足下列条件:(1)相切;(2)相交;(3)外离;(4)内含.分析将所给圆的方程化为圆的标准方程,求出两圆的圆心与半径后结合两圆的位置关系列式求解.
解圆C1,C2的方程,经配方后可得C1:(x-a)2+(y-1)2=16,C2:(x-2a)2+(y-1)2=1,∴圆心C1(a,1),C2(2a,1),半径r1=4,r2=1.
(1)当|C1C2|=r1+r2=5,即a=5时,两圆外切;当|C1C2|=r1-r2=3,即a=3时,两圆内切.(2)当3<|C1C2|<5,即35,即a>5时,两圆外离.(4)当|C1C2|<3,即0规律方法　判断两圆位置关系的方法判断两圆位置关系的方法有代数法与几何法两种,我们常用几何法而不用代数法.因为用代数法时,若两圆方程消元后得到的方程只有一个解时,无法直接确定两圆是外切还是内切,因此常用几何法判断,其方法如下:(1)将圆的方程化为标准式,求出圆心和半径;(2)计算圆心距、半径和、半径差的绝对值;(3)利用圆心距、半径和、半径差的绝对值判定两圆的位置关系.
变式训练1已知两圆C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0的方程,判断两圆的位置关系.
解 (方法1　几何法)把两圆的方程分别配方,化为标准方程是(x-1)2+y2=4,
故r1-r2<|C1C2|(方法2　代数法)联立两圆方程,得
交点个数为2,故两圆相交.
探究点二两圆相交问题
【例2】已知两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0.(1)证明两圆相交;(2)求两圆的公共弦所在的直线方程以及公共弦长.分析将所给圆的方程化为标准式,求出两圆的圆心坐标与半径,通过判断两圆的圆心距与半径和、半径差的关系证明两圆相交,而公共弦所在的直线方程以及公共弦的长度需要先将两方程相减求得公共弦方程,结合公共弦方程求弦长.
(1)证明两圆方程配方化为标准方程可得C1:(x-1)2+(y+5)2=50, C2:(x+1)2+(y+1)2=10.
(2)解将两圆方程相减,得两圆公共弦所在的直线方程为x-2y+4=0.
变式探究1本例中若两圆相交于A,B两点,求经过A,B两点,且面积最小的圆的方程.
两式相减得x=2y-4,③把③代入②得y2-2y=0,解得y1=0,y2=2.
经过A,B两点且面积最小的圆的方程即为以线段AB为直径的圆,其圆心坐标为(-2,1),半径为r= ,故所求的圆的方程为(x+2)2+(y-1)2=5.
变式探究2本例中若两圆相交于A,B两点,求经过A,B两点,且圆心在直线x+y=0上的圆的方程.
解设所求的圆的方程为x2+y2-2x+10y-24+λ(x2+y2+2x+2y-8)=0(λ≠-1),整理可得(1+λ)x2+(1+λ)y2+(2λ-2)x+(2λ+10)y-8λ-24=0.
规律方法　求两圆的公共弦长及公共弦所在直线的方程的方法求两圆的公共弦长及公共弦所在直线的方程一般不用求交点的方法,常用如下方法:
[提醒]求两圆的公共弦所在直线的方程,只有两圆相交时,才能通过消去二次项得到两圆的公共弦所在直线的方程.
变式训练2两圆相交于两点A(1,3)和B(m,-1),两圆圆心都在直线x-y+c=0上,则m+c的值为　　　　　.
解析由题意知直线AB与直线x-y+c=0垂直,∴kAB×1=-1,
∵AB的中点在直线x-y+c=0上,∴3-1+c=0,解得c=-2,∴m+c=5-2=3.
探究点三两圆相切问题
圆的方程.分析设出圆的方程,利用两圆外切的条件以及直线与圆相切的条件,建立方程组求解.
解设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),由题知所求圆与圆x2+y2-2x=0外切,将圆x2+y2-2x=0化为(x-1)2+y2=1,得该圆圆心为(1,0),半径为1,
规律方法　求解两圆相切问题的两个步骤:(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须分两圆内切还是外切两种情况讨论.(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
变式训练3(1)求以(3,-4)为圆心,且与圆x2+y2=64内切的圆的半径;(2)若圆C1:(x-m)2+(y+2)2=9与圆C2:(x+1)2+(y-m)2=4外切,求m的值.
解 (1)设所求圆的半径为r,则 =|8-r|,所以r=3或r=13.即所求圆的半径为3或13.
(2)由题可得圆C1的圆心为(m,-2),半径为r1=3,圆C2的圆心为(-1,m),半径为r2=2.由题意得|C1C2|=5,即(m+1)2+(-2-m)2=25,解得m=2或m=-5.
1.知识清单:圆与圆的位置关系2.方法归纳:利用几何法、代数法判断圆与圆的位置关系、求两圆的公共弦长及两圆相切问题,利用代数法求公共弦所在直线的方程,利用圆系方程求解过两圆交点的圆的方程.3.注意事项:利用代数法判断两圆位置关系时,将两圆方程联立后的方程组,消元后,若方程只有一个解,不能判断两圆是内切还是外切;若所得方程无解,则不能判断两圆是内含还是外离,此时需要结合图形判断.利用圆系方程求圆的方程时,不要忘记检验与参数结合的圆是否满足题意.求解两圆相切问题,应明确是内切还是外切.
1.圆O1:(x-1)2+y2=1与圆O2:x2+(y+2)2=4的位置关系是(　　)A.外离B.外切C.相交D.内切
解析圆心O1为(1,0),半径为r1=1,圆心O2为(0,-2),半径为r2=2,则圆心距为|O1O2|= ,r1+r2=3,r2-r1=1,所以r2-r1<|O1O2|2.已知圆C1:x2+y2+2x-6y-26=0,C2:x2+y2-4x+2y+4=0,则两圆的位置关系为(　　)A.两圆内切B.两圆相交C.两圆外切D.两圆相离
解析 ∵圆C1:x2+y2+2x-6y-26=0的圆心为C1(-1,3),半径r1=6,圆C2:x2+y2-4x+2y+4=0的圆心为C2(2,-1),半径r2=1,
又r1-r2=5,∴|C1C2|=r2-r1=5,∴圆C1与C2内切.故选A.
3.圆心为C(2,0)的圆与圆x2+y2+4x-6y+4=0外切,则圆C的方程为(　　)A.x2+y2-4x=0B.x2+y2-4x+2=0C.x2+y2+4x+2=0D.x2+y2+4x=0
解析圆x2+y2+4x-6y+4=0的圆心为M(-2,3),半径为r=3,则|CM|= =5,故圆C的半径为5-3=2,所以圆C的标准方程为(x-2)2+y2=4,整理得x2+y2-4x=0.故选A.
4.已知圆C1:x2+y2=1和圆C2:x2+(y-2)2=r2(r>0),若圆C1和C2有公共点,则r的取值范围是(　　)A.(0,1]B.(0,3]C.[1,3]D.[1,+∞)
解析若圆C1和C2有公共点时,两圆相切或相交,圆心C1(0,0),半径R=1,圆心C2(0,2),半径为r,则|C1C2|= =2.若两圆有公共点,则满足r-R≤|C1C2|≤R+r,即r-1≤2≤1+r,得1≤r≤3.故选C.
5.若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦长为2 ,则a=　　　　.

相关课件更多