

所属成套资源:新高考数学一轮复习课时过关练习 (含解析)
- 新高考数学一轮复习课时过关练习第03章 一元函数的导数及其应用第3节 导数与函数的极值、最值 (含解析) 试卷 0 次下载
- 新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第1节 任意角和弧度制及三角函数的概念 (含解析) 试卷 0 次下载
- 新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第3节 三角恒等变换第1课时 两角和与差的正弦、余弦和正切 (含解析) 试卷 0 次下载
- 新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第3节 三角恒等变换第2课时 简单的三角恒等变换 (含解析) 试卷 0 次下载
- 新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第4节 三角函数的图象与性质 (含解析) 试卷 0 次下载
新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第2节 同角三角函数的基本关系及诱导公式 (含解析)
展开
这是一份新高考数学一轮复习课时过关练习第04章 三角函数、解三角形第2节 同角三角函数的基本关系及诱导公式 (含解析),共17页。试卷主要包含了理解同角三角函数的基本关系式等内容,欢迎下载使用。
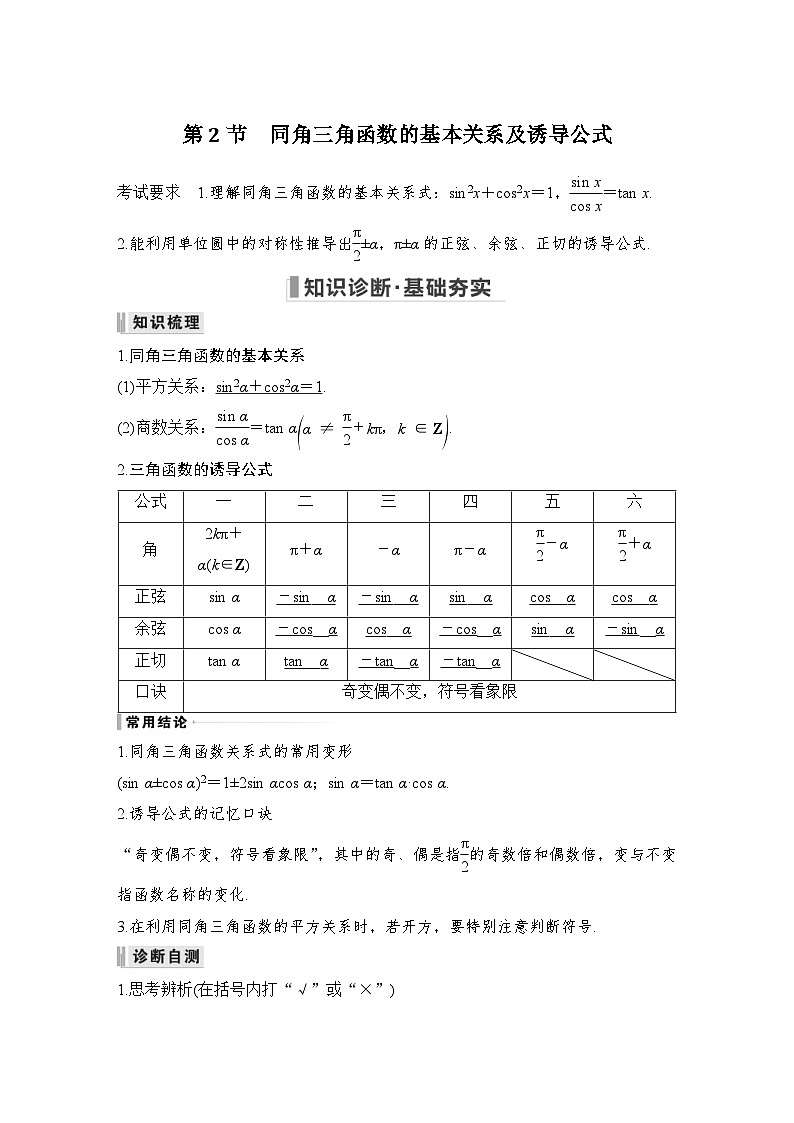
第2节 同角三角函数的基本关系及诱导公式
考试要求 1.理解同角三角函数的基本关系式:sin2x+cos2x=1,=tan x.
2.能利用单位圆中的对称性推导出±α,π±α的正弦、余弦、正切的诱导公式.
1.同角三角函数的基本关系
(1)平方关系:sin2α+cos2α=1.
(2)商数关系:=tan α.
2.三角函数的诱导公式
公式
一
二
三
四
五
六
角
2kπ+α(k∈Z)
π+α
-α
π-α
-α
+α
正弦
sin α
-sin__α
-sin__α
sin__α
cos__α
cos__α
余弦
cos α
-cos__α
cos__α
-cos__α
sin__α
-sin__α
正切
tan α
tan__α
-tan__α
-tan__α
口诀
奇变偶不变,符号看象限
1.同角三角函数关系式的常用变形
(sin α±cos α)2=1±2sin αcos α;sin α=tan α·cos α.
2.诱导公式的记忆口诀
“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.
3.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.
1.思考辨析(在括号内打“√”或“×”)
(1)若α,β为锐角,则sin2α+cos2β=1.( )
(2)sin(π+α)=-sin α成立的条件是α为锐角.( )
(3)若α∈R,则tan α=恒成立.( )
(4)若sin(kπ-α)=(k∈Z),则sin α=.( )
答案 (1)× (2)× (3)× (4)×
解析 (1)对任意的角α,sin2α+cos2α=1.
(2)中对于任意α∈R,恒有sin(π+α)=-sin α.
(3)中当α的终边落在y轴上时,商数关系不成立.
(4)当k为奇数时,sin α=,
当k为偶数时,sin α=-.
2.(多选)已知x∈R,则下列等式恒成立的是( )
A.sin(-x)=sin x
B.sin=cos x
C.cos=-sin x
D.cos(x-π)=-cos x
答案 CD
解析 sin(-x)=-sin x,故A不成立;
sin=-cos x,故B不成立;
cos=-sin x,故C成立;
cos(x-π)=-cos x,故D成立.
3.(2022·南昌一模)已知3sin+sin(θ+π)=0,θ∈(-π,0),则sin θ=( )
A.- B.-
C. D.
答案 A
解析 ∵3sin+sin(θ+π)=0,
∴3cos θ-sin θ=0,
∴tan θ==3,
∵θ∈(-π,0),sin2θ+cos2θ=1,
所以sin θ=-.
4.(2021·沈阳郊联体一模)已知2sin(π-α)=3sin,则sin2α-sin 2α-cos2α=( )
A. B.- C.- D.
答案 B
解析 由条件得2sin α=3cos α,
即tan α=,
故原式=
=
===-.
5.化简·sin(α-π)·cos(2π-α)的结果为________.
答案 -sin2α
解析 原式=·(-sin α)·cos α=-sin2α.
6.(易错题)已知sin αcos α=,且<α<,则cos α-sin α的值为________.
答案
解析 ∵<α<,∴cos α<0,sin α<0且cos α>sin α,
∴cos α-sin α>0.
又(cos α-sin α)2=1-2sin αcos α=1-2×=,
∴cos α-sin α=.
考点一 同角三角函数基本关系式的应用
角度1 切弦互化
例1 (1)已知α是三角形的内角,且tan α=-,则sin α+cos α的值为________.
答案 -
解析 由tan α=-,得sin α=-cos α,
将其代入sin2α+cos2α=1,得cos2α=1,
所以cos2α=,易知cos α<0,
所以cos α=-,sin α=,
故sin α+cos α=-.
(2)已知sin+3cos(π-θ)=sin(-θ),则sin θcos θ+cos2θ=( )
A. B. C. D.
答案 C
解析 由已知sin+3cos(π-θ)=sin(-θ)⇒cos θ-3cos θ=-sin θ⇒tan θ=2,
则sin θcos θ+cos2θ===.
角度2 “和”“积”转换
例2 (1)已知sin αcos α=,且<α<,则cos α-sin α的值为( )
A. B.± C.- D.-
答案 D
解析 ∵sin αcos α=,
∴(cos α-sin α)2=cos2α-2sin αcos α+sin2α=1-2sin αcos α=1-2×=,
∵<α<,∴cos α<sin α,
即cos α-sin α<0,∴cos α-sin α=-.
(2)(多选)(2021·滨州模拟)已知θ∈(0,π),sin θ+cos θ=,则下列结论正确的是( )
A.sin θ= B.cos θ=-
C.tan θ=- D.sin θ-cos θ=
答案 ABD
解析 由题意知sin θ+cos θ=,
∴(sin θ+cos θ)2=1+2sin θcos θ=,
∴2sin θcos θ=-<0,
又∵θ∈(0,π),∴<θ<π,
∴sin θ-cos θ>0,
∴sin θ-cos θ=
===,
∴sin θ=,cos θ=-.
∴tan θ=-,∴A、B、D正确.
感悟提升 1.(1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tan α可以实现角α的弦切互化.
(2)形如,asin2x+bsin xcos x+ccos2x等类型可进行弦化切.
2.注意公式的逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.
3.应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二.
训练1 (1)若tan α=,则cos2α+2sin 2α等于( )
A. B. C.1 D.
答案 A
解析 tan α=,则cos2α+2sin 2α==
==.
(2)已知sin α,cos α是方程3x2-2x+a=0的两个根,则实数a的值为( )
A. B.- C. D.
答案 B
解析 由题可得,sin α+cos α=,sin αcos α=.
所以sin2α+cos2α=(sin α+cos α)2-2sin αcos α=-=1,解得a=-.
考点二 诱导公式的应用
1.sin 570°的值是( )
A.- B. C. D.-
答案 A
解析 sin 570°=sin(720°-150°)
=-sin 150°=-.
2.化简的结果是( )
A.-1 B.1 C.tan α D.-tan α
答案 C
解析 原式=
==tan α.
3.已知sin=,则cos等于( )
A. B. C.- D.-
答案 B
解析 因为sin=,
所以cos=sin
=sin=.
4.设f(α)=(1+2sin α≠0),则f=________.
答案
解析 因为f(α)=
===,
所以f=
===.
感悟提升 (1)诱导公式的两个应用
①求值:负化正,大化小,化到锐角为终了.
②化简:统一角,统一名,同角名少为终了.
(2)含2π整数倍的诱导公式的应用
由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算.如cos(5π-α)=cos(π-α)=-cos α.
考点三 同角关系式和诱导公式的综合应用
例3 (1)(2020·全国Ⅰ卷)已知α∈(0,π),且3cos 2α-8cos α=5,则sin α=( )
A. B. C. D.
答案 A
解析 由3cos 2α-8cos α=5,
得3(2cos2α-1)-8cos α=5,
即3cos2α-4cos α-4=0,
解得cos α=-或cos α=2(舍去).
又因为α∈(0,π),
所以sin α===.
(2)已知α是第三象限角,且cos α=-.则的值为________.
答案
解析 ∵α是第三象限角,
∴sin α=-=-,
==
==.
(3)已知cos=a(|a|≤1),则cos+sin的值是________.
答案 0
解析 ∵cos=cos=-cos=-a,
sin=sin
=cos=a,
∴cos+sin=0.
感悟提升 1.利用同角三角函数关系式和诱导公式求值或化简时,关键是寻求条件、结论间的联系,灵活使用公式进行变形.注意角的范围对三角函数值符号的影响.
2.用诱导公式求值时,要善于观察所给角之间的关系,利用整体代换的思想简化解题过程.常见的互余关系有-α与+α,+α与-α,+α与-α等,常见的互补关系有-θ与+θ,+θ与-θ,+θ与-θ等.
训练2 (1)(多选)给出下列四个结论,其中正确的结论是( )
A.sin(π+α)=-sin α成立的条件是角α是锐角
B.若cos(nπ-α)=(n∈Z),则cos α=
C.若α≠(k∈Z),则tan=
D.若sin α+cos α=1,则sinnα+cosnα=1
答案 CD
解析 由诱导公式二知α∈R时,sin(π+α)=-sin α,所以A错误;
当n=2k(k∈Z)时,cos(nπ-α)=cos(-α)=cos α,此时cos α=;
当n=2k+1(k∈Z)时,cos(nπ-α)=cos[(2k+1)π-α]=cos(π-α)=-cos α,此时cos α=-,所以B错误;
若α≠(k∈Z),则tan===-,所以C正确;
将等式sin α+cos α=1两边平方,得sin αcos α=0,所以sin α=0或cos α=0.
若sin α=0,则cos α=1,此时sinnα+cosnα=1;
若cos α=0,则sin α=1,此时sinnα+cosnα=1,故sinnα+cosnα=1,所以D正确.
(2)已知sin α+cos α=-,且<α<π,则+的值为________.
答案
解析 由sin α+cos α=-,
平方得sin αcos α=-,
∵<α<π,∴sin α-cos α
==,
∴+=-===.
1.sin 1 050°等于( )
A. B.- C. D.-
答案 B
解析 sin 1 050°=sin(3×360°-30°)=-sin 30°=-.
2.已知sin=,则cos的值是( )
A.- B. C. D.-
答案 A
解析 ∵sin=,∴cos=cos=-sin=-.故选A.
3.(多选)若cos(π-α)=-,则( )
A.sin(-α)= B.sin=-
C.cos(π+α)=- D.cos(α-π)=-
答案 CD
解析 由cos(π-α)=-可得cos α=,则sin α=±.
A中,sin(-α)=-sin α=±,不正确.
B中,sin=cos α=,不正确.
C中,cos(π+α)=-cos α=-,正确.
D中,cos(α-π)=-cos α=-,正确.
4.(2022·广州模拟)若点P(cos α,sin α)在直线y=-2x上,则sin的值等于( )
A.- B. C.- D.
答案 A
解析 由点P(cos α,sin α)在直线y=-2x上,得tan α=-2,故sin=cos 2α===-.
5.(多选)(2021·临沂质检)已知sin(π+θ)=cos(2π-θ),θ∈,则θ可能等于( )
A.- B.- C. D.
答案 AD
解析 ∵sin(π+θ)=cos(2π-θ),
∴-sin θ=cos θ,∴tan θ=-,
∵θ∈,∴θ=-或θ=.
6.(多选)在△ABC中,下列结论正确的是( )
A.sin(A+B)=sin C
B.sin =cos
C.tan(A+B)=-tan C
D.cos(A+B)=cos C
答案 ABC
解析 在△ABC中,有A+B+C=π,
则sin(A+B)=sin(π-C)=sin C,A正确;
sin =sin=cos ,B正确;
tan(A+B)=tan(π-C)=-tan C,C正确;
cos(A+B)=cos(π-C)=-cos C,D错误.故选ABC.
7.(2022·重庆诊断)已知sin α+cos α=-,则tan α+等于( )
A.2 B. C.-2 D.-
答案 A
解析 由已知得1+2sin αcos α=2,
∴sin αcos α=,
∴tan α+=+
===2.
8.已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos 2α=,则|a-b|=( )
A. B. C. D.1
答案 B
解析 由cos 2α=,得cos2α-sin2α=,
∴=,即=,
∴tan α=±,即=±,
∴|a-b|=,故选B.
9.若=,则tan θ=________.
答案 -3
解析 因为==,
所以2(sin θ+cos θ)=sin θ-cos θ,
所以sin θ=-3cos θ,所以tan θ=-3.
10.若tan α=-2,则cos2α+2sin 2α=________.
答案 -
解析 原式=
=
===-.
11.已知-<α<0,sin α+cos α=, 则的值为________.
答案
解析 由题意,因为sin α+cos α=,所以1+2sin αcos α=,
所以2sin αcos α=-,
所以(cos α-sin α)2=1-2sin αcos α=,
又因为-<α<0,所以sin α<0,cos α>0,
所以cos α-sin α=,
所以=
=.
12.已知θ是第四象限角,且sin=,则tan=________.
答案 -
解析 由题意,得cos=,
∴tan=.
∴tan=tan
=-=-.
13.(2021·哈尔滨一模)若sin α+cos α=,α∈(0,π),则的值为( )
A.-3 B.- C. D.3
答案 A
解析 因为sin α+cos α=,所以sin2α+cos2α=sin2α+=1,
可得25sin2α-5sin α-12=0,解得sin α=或-,
又因为α∈(0,π) ,所以sin α=,
所以cos α=-=-,
则=
=
===-3,故选A.
14.(多选)定义:角θ与φ都是任意角,若满足θ+φ=,则称θ与φ“广义互余”.已知sin(π+α)=-,下列角β中,可能与角α“广义互余”的是( )
A.sin β= B.cos(π+β)=
C.tan β= D.tan β=
答案 AC
解析 ∵sin(π+α)=-sin α=-,
∴sin α=,cos α=±,
∴若α+β=,则β=-α.
sin β=sin=cos α可能成立,角β可能与角α“广义互余”,故A符合条件;
若B符合,则cos(π+β)=-cos=-sin α=-,与cos(π+β)=矛盾,故B不符合条件;
对于C,tan β=,即sin β=cos β,又sin2β+cos2β=1,故sin β=±,即C符合条件;
tan β=,即sin β=cos β,又sin2β+cos2β=1,故sin β=±,故D不符合条件.
15.已知α为第二象限角,则cos α+sin α=________.
答案 0
解析 原式=cos α+sin α=cos α+sin α,
因为α是第二象限角,
所以sin α>0,cos α<0,
所以cos α+sin α=-1+1=0,即原式等于0.
16.如图是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的内角为θ,大正方形的面积是1,小正方形的面积是,则sin2θ-cos2θ的值是________.
答案 -
解析 由题意可知,拼图中的每个直角三角形的长直角边为cos θ,短直角边为sin θ,小正方形的边长为cos θ-sin θ,
∵小正方形的面积是,∴(cos θ-sin θ)2=,
∵θ为直角三角形中较小的锐角,
∴cos θ>sin θ ,∴cos θ-sin θ=,
又∵(cos θ-sin θ)2=1-2sin θcos θ=,
∴2sin θcos θ=,∴1+2sin θcos θ=,
即(cos θ+sin θ)2=,∴cos θ+sin θ=,
∴sin2θ-cos2θ=(cos θ+sin θ)(sin θ-cos θ)=-.
相关试卷
这是一份新高考数学一轮复习三角函数巩固练习第2练 同角三角函数的基本关系及诱导公式(含解析),共21页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份第2练 同角三角函数的基本关系及诱导公式《2024新高考数学一轮复习同步精练之三角函数与解三角形》(解析版),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份新高考数学一轮复习课时讲练 第4章 第2讲 同角三角函数的基本关系与诱导公式 (含解析),共14页。试卷主要包含了同角三角函数的基本关系,六组诱导公式等内容,欢迎下载使用。










