

新高考数学一轮复习课时过关练习第08章 平面解析几何第8节 抛物线 (含解析)
展开第8节 抛物线
考试要求 1.了解抛物线的定义、几何图形和标准方程,以及它们的简单几何性质.2.通过圆锥曲线与方程的学习,进一步体会数形结合的思想.
1.抛物线的定义
(1)平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(2)其数学表达式:{M||MF|=d}(d为点M到准线l的距离).
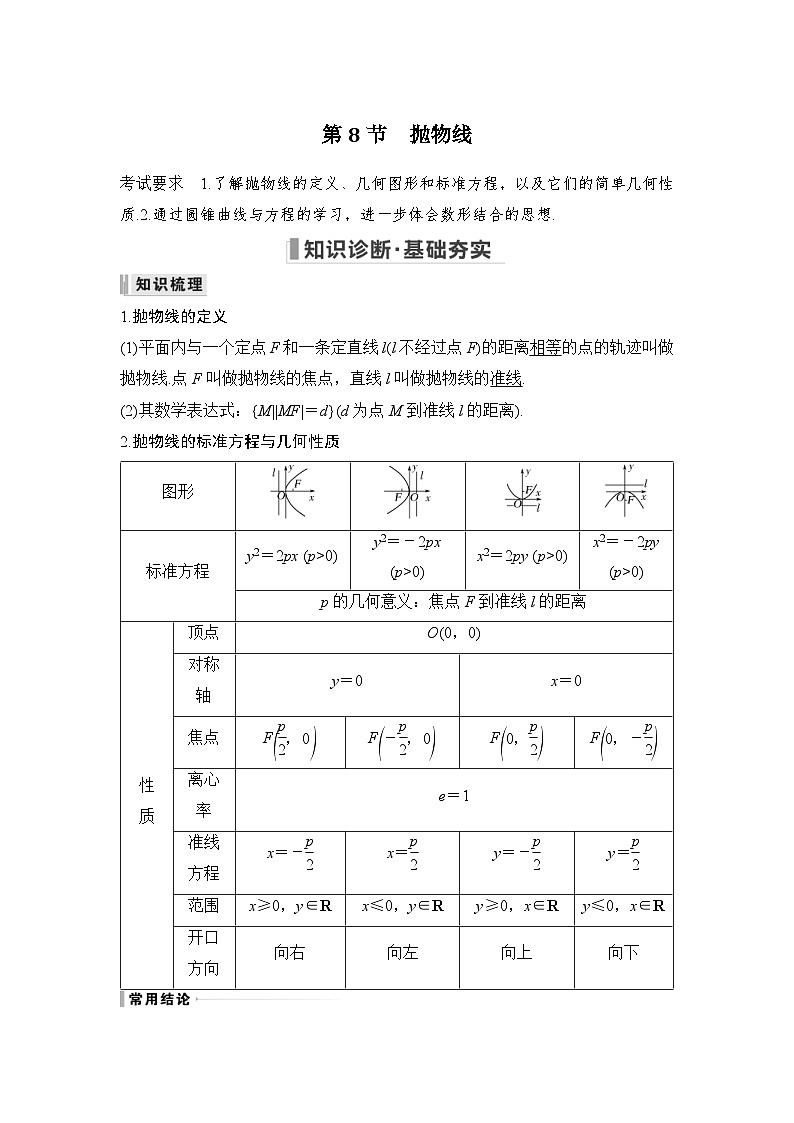
2.抛物线的标准方程与几何性质
图形
标准方程
y2=2px (p>0)
y2=-2px (p>0)
x2=2py (p>0)
x2=-2py (p>0)
p的几何意义:焦点F到准线l的距离
性
质
顶点
O(0,0)
对称轴
y=0
x=0
焦点
F
F
F
F
离心率
e=1
准线方程
x=-
x=
y=-
y=
范围
x≥0,y∈R
x≤0,y∈R
y≥0,x∈R
y≤0,x∈R
开口方向
向右
向左
向上
向下
1.通径:过焦点且垂直于对称轴的弦长等于2p,通径是过焦点最短的弦.
2.抛物线y2=2px(p>0)上一点P(x0,y0)到焦点F的距离|PF|=x0+,也称为抛物线的焦半径.
1.思考辨析(在括号内打“√”或“×”)
(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线.( )
(2)方程y=ax2(a≠0)表示的曲线是焦点在x轴上的抛物线,且其焦点坐标是,准线方程是x=-.( )
(3)抛物线既是中心对称图形,又是轴对称图形.( )
(4)若直线与抛物线只有一个交点,则直线与抛物线一定相切.( )
答案 (1)× (2)× (3)× (4)×
解析 (1)当定点在定直线上时,轨迹为过定点F与定直线l垂直的一条直线,而非抛物线.
(2)方程y=ax2(a≠0)可化为x2=y,是焦点在y轴上的抛物线,且其焦点坐标是,准线方程是y=-.
(3)抛物线是只有一条对称轴的轴对称图形.
(4)一条直线平行于抛物线的对称轴,此时与抛物线只有一个交点,但不相切.
2.(易错题)抛物线y=-x2的焦点坐标是( )
A.(0,-1) B.(0,1)
C.(1,0) D.(-1,0)
答案 A
解析 抛物线y=-x2的标准方程为x2=-4y,开口向下,p=2,=1,故焦点为(0,-1).
3.(多选)顶点在原点,对称轴为坐标轴且过点P(-2,3)的抛物线的标准方程是( )
A.y2=x B.x2=y
C.y2=-x D.x2=-y
答案 BC
解析 设抛物线的标准方程是y2=kx或x2=my,代入点P(-2,3),解得k=-,m=,所以y2=-x或x2=y.
4.(2020·新高考全国Ⅰ卷)斜率为的直线过抛物线C:y2=4x的焦点,且与C交于A,B两点,则|AB|=________.
答案
解析 由题意得,抛物线焦点为F(1,0),
设直线AB的方程为
y=(x-1).
由得3x2-10x+3=0.
设A(x1,y1),B(x2,y2),
则x1+x2=,
所以|AB|=x1+x2+2=.
5.(2021·新高考Ⅰ卷)已知O为坐标原点,抛物线C:y2=2px(p>0)的焦点为F,P为C上一点,PF与x轴垂直,Q为x轴上一点,且PQ⊥OP.若|FQ|=6,则C的准线方程为________.
答案 x=-
解析 法一 由题意易得|OF|=,|PF|=p,∠OPF=∠PQF,所以tan∠OPF=tan∠PQF,所以=,即=,解得p=3,所以C的准线方程为x=-.
法二 由题意易得|OF|=,|PF|=p,|PF|2=|OF|·|FQ|,即p2=·6,解得p=3或p=0(舍去),
所以C的准线方程为x=-.
6.(2022·龙岩一模)已知抛物线y2=4x的焦点为F,准线与x轴的交点为A,以AF为直径的圆在第一象限交抛物线于点B,则·的值等于________.
答案 6-2
解析 设B(x0,y0).由方程组
消去y并整理,
得x2+4x-1=0(x≥0),解得x0=-2.
由题意,得F(1,0),A(-1,0),
∴=(-2,0),=(x0-1,y0).
∴·=(-2,0)·(x0-1,y0)=-2(x0-1)=2-2x0=2-2(-2)=6-2.
考点一 抛物线的定义和标准方程
1.设抛物线y2=2px的焦点在直线2x+3y-8=0上,则该抛物线的准线方程为( )
A.x=-4 B.x=-3
C.x=-2 D.x=-1
答案 A
解析 直线2x+3y-8=0与x轴的交点为(4,0),∴抛物线y2=2px的焦点为(4,0),∴准线方程为x=-4.
2.动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹方程为________.
答案 y2=4x
解析 设动圆的圆心坐标为(x,y),则圆心到点(1,0)的距离与到直线x=-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹方程为y2=4x.
3.如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A、B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为________.
答案 y2=3x
解析 如图,分别过A、B作AA1⊥l于A1,BB1⊥l于B1,由抛物线的定义知:|AF|=|AA1|,|BF|=|BB1|,∵|BC|=2|BF|,∴|BC|=2|BB1|,∴∠BCB1=30°,∴∠AFx=60°,连接A1F,则△AA1F为等边三角形,过F作FF1⊥AA1于F1,则F1为AA1的中点,设l交x轴于K,则|KF|=|A1F1|=|AA1|=|AF|,即p=,∴抛物线方程为y2=3x.
4.(2022·广州模拟)已知抛物线x2=2py(p>0)的焦点为F,准线为l,点P(4,y0)在抛物线上,K为l与y轴的交点,且|PK|=|PF|,则y0=________,p=________.
答案 2 4
解析 作PM⊥l,垂足为M,由抛物线定义知|PM|=|PF|,又知|PK|=|PF|,
∴在Rt△PKM中,sin∠PKM===,
∴∠PKM=45°,∴△PMK为等腰直角三角形,
∴|PM|=|MK|=4,
又知点P在抛物线x2=2py(p>0)上,
∴解得
感悟提升 求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数p,只需一个条件就可以确定抛物线的标准方程.
考点二 抛物线的几何性质及应用
角度1 焦半径和焦点弦
例1 (1)已知点F为抛物线C:y2=4x的焦点,过点F的直线l交抛物线C于A,B两点,且=t(t>1),|AB|=,则t=( )
A.2 B.3 C.4 D.5
答案 B
解析 ∵焦点F(1,0),设直线l为x=λy+1(λ≠0),代入抛物线方程得y2-4λy-4=0.
设A(x1,y1),B(x2,y2),由韦达定理得y1y2=-4,①
由=t,即(1-x1,-y1)=t(x2-1,y2),有y1=-ty2,②
∴由①②得y2=,y1=-2或y2=-,y1=2,即x1=t,x2=,
∴|AB|=x1+x2+p=+t+2=,化简得3t2-10t+3=0,∴t=3或t=(舍).
(2)在平面直角坐标系xOy中,双曲线-=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为________.
答案 y=±x
解析 设A(x1,y1),B(x2,y2),
由抛物线的定义:
|AF|=y1+,|BF|=y2+,|OF|=,
所以|AF|+|BF|=y1++y2+=y1+y2+p=4|OF|=2p,
可得:y1+y2=p,
联立方程:⇒-=1⇒-+1=0,
由根与系数的关系得y1+y2=-=·b2=p,
∴p=p⇒=⇒=.
∴双曲线渐近线方程为y=±x.
角度2 与抛物线有关的最值问题
例2 (1)若在抛物线y2=-4x上存在一点P,使其到焦点F的距离与到A(-2,1)的距离之和最小,则该点的坐标为________.
答案
解析 如图,∵y2=-4x,∴p=2,焦点坐标为(-1,0).依题意可知当A,P及P到准线的垂足三点共线时,点P与点F、点P与点A的距离之和最小,故点P的纵坐标为1.将y=1代入抛物线方程求得x=-,则点P的坐标为.
(2)设P是抛物线y2=4x上的一个动点,则点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________.
答案
解析 如图,易知抛物线的焦点为F(1,0),准线是x=-1,由抛物线的定义知点P到直线x=-1的距离等于点P到F的距离.于是,问题转化为在抛物线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小,显然,连接AF与抛物线相交的点即为满足题意的点,此时最小值为=.
(3)已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为________.
答案 2
解析 由题意知,抛物线的准线l:y=-1,过点A作AA1⊥l交l于点A1,过点B作BB1⊥l交l于点B1,设弦AB的中点为M,过点M作MM1⊥l交l于点M1,则|MM1|=.因为|AB|≤|AF|+|BF|(F为抛物线的焦点),即|AF|+|BF|≥6,所以|AA1|+|BB1|≥6,2|MM1|≥6,|MM1|≥3,故点M到x轴的距离d≥2,故最短距离为2.
感悟提升 与抛物线有关的最值问题的两个转化策略
转化策略一:将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”“三角形两边之和大于第三边”,使问题得以解决.
转化策略二:将抛物线上的点到焦点的距离转化为到准线的距离,利用“与直线上所有点的连线中垂线段最短”原理解决.
训练1 (1)若抛物线y2=4x的准线为l,P是抛物线上任意一点,则P到准线l的距离与P到直线3x+4y+7=0的距离之和的最小值是( )
A.2 B. C. D.3
答案 A
解析 由抛物线定义可知点P到准线l的距离等于点P到焦点F的距离,由抛物线y2=4x及直线方程3x+4y+7=0可得直线与抛物线相离.
∴点P到准线l的距离与点P到直线3x+4y+7=0的距离之和的最小值为点F(1,0)到直线3x+4y+7=0的距离,即=2.
(2)已知抛物线y2=4x,过焦点F的直线与抛物线交于A,B两点,过A,B分别作y轴的垂线,垂足分别为C,D,则|AC|+|BD|的最小值为________.
答案 2
解析 由题意知F(1,0),|AC|+|BD|=|AF|+|FB|-2=|AB|-2,即|AC|+|BD|取得最小值时当且仅当|AB|取得最小值.依抛物线定义知,当|AB|为通径,即|AB|=2p=4时为最小值,所以|AC|+|BD|的最小值为2.
考点三 直线与抛物线的综合问题
例3 已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.
(1)若|AF|+|BF|=4,求直线l的方程;
(2)若=3,求|AB|.
解 设直线l的方程为y=x+t,A(x1,y1),B(x2,y2).
(1)由题设得F,故|AF|+|BF|=x1+x2+.
又|AF|+|BF|=4,所以x1+x2=.
由可得9x2+12(t-1)x+4t2=0,
其中Δ=144(1-2t)>0,
则x1+x2=-.
从而-=,得t=-(满足Δ>0).
所以l的方程为y=x-.
(2)由=3可得y1=-3y2.
由可得y2-2y+2t=0,
其中Δ=4-8t>0,
所以y1+y2=2,从而-3y2+y2=2,
故y2=-1,y1=3.
代入C的方程得x1=3,x2=.
所以A(3,3),B,故|AB|=.
感悟提升 1.有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点,可直接使用公式|AB|=x1+x2+p,若不过焦点,则必须用一般弦长公式.
2.涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”、“整体代入”等解法.
提醒 涉及弦的中点、斜率时一般用“点差法”求解.
训练2 (2022·湖州模拟)如图,已知抛物线x2=y,点A,B,抛物线上的点P(x,y).过点B作直线AP的垂线,垂足为Q.
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
解 (1)设直线AP的斜率为k,
k==x-,因为-<x<,
所以直线AP斜率的取值范围是(-1,1).
(2)联立直线AP与BQ的方程
解得点Q的横坐标是xQ=.
因为|PA|==(k+1),
|PQ|=(xQ-x)
=-,
所以|PA|·|PQ|=-(k-1)(k+1)3.
令f(k)=-(k-1)(k+1)3,
因为f′(k)=-(4k-2)(k+1)2,
所以f(k)在区间上单调递增,上单调递减,
因此当k=时,|PA|·|PQ|取得最大值.
抛物线的几个“二级结论”的应用
抛物线焦点弦的有关性质是高中数学的重要部分,了解和掌握相关结论,在解题时可迅速打开思路,抛物线焦点弦的常见结论如下:
设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),则
(1)x1·x2=.
(2)y1·y2=-p2.
(3)|AB|=x1+x2+p=(α是直线AB的倾斜角).
(4)+=为定值(F是抛物线的焦点).
例1 过抛物线y2=4x的焦点F的直线l与抛物线交于A,B两点,若|AF|=2|BF|,则|AB|等于( )
A.4 B. C.5 D.6
答案 B
解析 [通法]易知直线l的斜率存在,设为k,则其方程为
y=k(x-1).
由得k2x2-(2k2+4)x+k2=0,
得xA·xB=1,①
因为|AF|=2|BF|,由抛物线的定义得xA+1=2(xB+1),
即xA=2xB+1,②
由①②解得xA=2,xB=,
所以|AB|=|AF|+|BF|
=xA+xB+p=.
[优解]法一 由对称性不妨设点A在x轴的上方,如图,设A,B在准线上的射影分别为D,C,作BE⊥AD于E,
设|BF|=m,直线l的倾斜角为θ,
则|AB|=3m,
由抛物线的定义知
|AD|=|AF|=2m,|BC|=|BF|=m,
所以cos θ==,所以tan θ=2.则sin2θ=8cos2θ,∴sin2θ=.又y2=4x,知2p=4,故利用弦长公式|AB|==.
法二 因为|AF|=2|BF|,所以+=+===1,解得|BF|=,|AF|=3,
故|AB|=|AF|+|BF|=.
例2 设F为抛物线C:y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为( )
A. B. C. D.
答案 D
解析 [通法]由已知得焦点坐标为F,因此直线AB的方程为y=,即4x-4y-3=0.
与抛物线方程联立,化简得4y2-12y-9=0,
故|yA-yB|==6.
因此S△OAB=|OF||yA-yB|=××6=.
[优解]由2p=3,及|AB|=
得|AB|===12.
原点到直线AB的距离
d=|OF|·sin 30°=,
故S△AOB=|AB|·d=×12×=.
1.抛物线x2=y的焦点到准线的距离是( )
A.2 B.1 C. D.
答案 D
解析 抛物线标准方程x2=2py(p>0)中p的几何意义为抛物线的焦点到准线的距离,又p=.故选D.
2.若抛物线y2=2px(p>0)的焦点是椭圆+=1的一个焦点,则p等于( )
A.2 B.3 C.4 D.8
答案 D
解析 由题意知,抛物线的焦点坐标为,
椭圆的焦点坐标为(±,0),
所以=,解得p=8.
3.(2020·全国Ⅲ卷)设O为坐标原点,直线x=2与抛物线C:y2=2px(p>0)交于D,E两点,若OD⊥OE,则C的焦点坐标为( )
A. B. C.(1,0) D.(2,0)
答案 B
解析 将x=2与抛物线方程y2=2px联立,可得y=±2,不妨设D(2,2),E(2,-2),由OD⊥OE,可得·=4-4p=0,解得p=1,所以抛物线C的方程为y2=2x.其焦点坐标为.
4.(多选)(2021·烟台调研)已知F是抛物线C:y2=16x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则( )
A.C的准线方程为x=-4
B.F点的坐标为(0,4)
C.|FN|=12
D.三角形ONF的面积为16(O为坐标原点)
答案 ACD
解析 不妨设点M位于第一象限,设抛物线的准线l与x轴交于点F′,作MB⊥l于点B,NA⊥l于点A.
由抛物线的解析式可得准线方程为x=-4,F点的坐标为(4,0),A正确,B错误.故|AN|=4,|FF′|=8,在直角梯形ANFF′中,中位线|BM|==6,
由抛物线的定义有|MF|=|MB|=6,结合题意,有|MN|=|MF|=6,
故|FN|=|FM|+|NM|=6+6=12,C正确,而|ON|==8,
SONF=×8×4=16,D正确.
5.设F为抛物线y2=2x的焦点,A,B,C为抛物线上三点,若F为△ABC的重心,则||+||+||的值为( )
A.1 B.2 C.3 D.4
答案 C
解析 依题意,设点A(x1,y1),B(x2,y2),C(x3,y3),
又焦点F,所以x1+x2+x3=3×=,
则||+||+||=++=(x1+x2+x3)+=+=3.
6.(多选)(2022·武汉模拟)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,A为C上一点,以F为圆心,|FA|为半径的圆交l于B,D两点.若△ABF的面积为9,则( )
A.|BF|=3
B.△ABF是等边三角形
C.点F到准线的距离为3
D.抛物线C的方程为y2=6x
答案 BCD
解析 因为|FA|为半径的圆交l于B,D两点,所以|FA|=|FB|;又|BF|=|FD|=|FA|,所以∠ABD=90°,|FA|=|AB|,可得△ABF为等边三角形,B正确;
过F作FC⊥AB交于C,则C为AB的中点,C的横坐标为,B的横坐标为-,所以A的横坐标为,代入抛物线可得y=3p2,|yA|=p,
△ABF的面积为9,即(xA-xB)|yA|=··p=9,解得p=3,所以抛物线的方程为y2=6x,D正确;
焦点坐标为,所以焦点到准线的距离为×2=3,C正确;
此时点A的横坐标为,所以|BF|=|AF|=|AB|=+=6,A不正确.
7.如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽________米.
答案 2
解析 建立如图平面直角坐标系,设抛物线方程为x2=-2py(p>0).
由题意将点A(2,-2)代入x2=-2py,得p=1,故x2=-2y.
设B(x,-3),代入x2=-2y中,得x=,故水面宽为2米.
8.已知直线l是抛物线y2=2px(p>0)的准线,半径为3的圆过抛物线顶点O和焦点F与l相切,则抛物线的方程为________.
答案 y2=8x
解析 ∵半径为3的圆与抛物线的准线l相切,
∴圆心到准线的距离等于3,
又∵圆心在OF的垂直平分线上,|OF|=,
∴+=3,∴p=4,故抛物线的方程为y2=8x.
9.直线l过抛物线C:y2=2px(p>0)的焦点F(1,0),且与C交于A,B两点,则p=________,+=________.
答案 2 1
解析 由题意知=1,从而p=2,
所以抛物线方程为y2=4x.
当直线AB的斜率不存在时,将x=1代入抛物线方程,解得|AF|=|BF|=2,
从而+=1.
当直线AB的斜率存在时,
设AB的方程为y=k(x-1),
联立
整理,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),
则
从而+=+===1.
综上,+=1.
10.已知过抛物线y2=2px(p>0)的焦点,斜率为2的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若=+λ,求λ的值.
解 (1)抛物线的焦点坐标为,则直线AB的方程是y=2,
与y2=2px联立,化简得4x2-5px+p2=0,
所以x1+x2=.又|AB|=x1+x2+p=9,
所以p=4,从而抛物线方程是y2=8x.
(2)由p=4,4x2-5px+p2=0得x2-5x+4=0.
又x1<x2,
从而x1=1,x2=4,y1=-2,y2=4,
从而A(1,-2),B(4,4).
设=(x3,y3),所以(x3,y3)=(1,-2)+λ(4,4)=(4λ+1,4λ-2),
又y=8x3,即[2(2λ-1)]2=8(4λ+1).
即(2λ-1)2=4λ+1,解得λ=0或λ=2.
11.(2022·北京昌平区模拟)已知抛物线C:y2=2px过点P(1,1),过点作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
(1)解 把P(1,1)代入y2=2px得p=,
∴抛物线C的方程为y2=x,
焦点坐标为,准线方程为x=-.
(2)证明 ∵BM⊥x轴,
∴设M(x1,y1),N(x2,y2),A(x1,yA),B(x1,yB),
根据题意显然有x1≠0.
若要证A为BM的中点,
只需证2yA=yB+y1即可,
左右同除以x1有=+,
即只需证明2kOA=kOB+kOM成立,其中kOA=kOP=1,kOB=kON.
当直线MN斜率不存在或斜率为零时,显然与抛物线只有一个交点不满足题意,所以直线MN斜率存在且不为零.
设直线MN:y=kx+(k≠0),
联立消y得,k2x2+(k-1)x+=0,
考虑Δ=(k-1)2-4××k2=1-2k,
由题可知有两交点,所以判别式大于零,所以k<.
由根与系数关系可知:x1+x2=,①
x1x2=.②
kOB+kOM=kON+kOM=+=+=2k+.
将①②代入上式,有2k+=2k+=2k+2(1-k)=2,
即kON+kOM=kOB+kOM=2=2kOA,
∴2yA=yB+y1恒成立,
∴A为BM的中点,得证.
12.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
答案 C
解析 ∵以MF为直径的圆过点(0,2),
∴点M在第一象限.
由|MF|=xM+=5,
可得M.
从而以MF为直径的圆的圆心N的坐标为.
∵点N的横坐标恰好等于圆的半径,
∴圆与y轴切于点(0,2),
从而2=,
即p2-10p+16=0,解得p=2或p=8,
∴抛物线C的方程为y2=4x或y2=16x.
13.(多选)(2022·青岛质检)设F是抛物线C:y2=4x的焦点,直线l过点F,且与抛物线C交于A,B两点,O为坐标原点,则下列结论正确的是( )
A.|AB|≥4
B.|OA|+|OB|>8
C.若点P(2,2),则|PA|+|AF|的最小值是3
D.△OAB面积的最小值是2
答案 ACD
解析 由题意知F(1,0),不妨设A在第一象限,
(1)若直线l斜率不存在,
则A(1,2),B(1,-2),
则|AB|=4,|OA|+|OB|=2|OA|=2,S△OAB=×4×1=2,显然B错误;
(2)若直线l存在斜率,设直线l的斜率为k,
则直线l的方程为y=k(x-1),显然k≠0,
联立方程组
消元得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),
则x1+x2==2+,
∴|AB|=x1+x2+2=4+>4,
原点O到直线l的距离d=,
∴S△OAB=×|AB|×d
=××
=2>2,
综上,|AB|≥4,S△OAB≥2,故A正确,D正确.
过点A向准线作垂线,垂足为N,
则|PA|+|AF|=|PA|+|AN|.
又P(2,2)在抛物线右侧,故当P,A,N三点共线时,|PA|+|AF|取得最小值3,故C正确.故选ACD.
14.已知曲线C:y=,D为直线y=-上的动点,过D作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点;
(2)若以E为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
(1)证明 设D,A(x1,y1),
则x=2y1.
因为y′=x,所以切线DA的斜率为x1,故=x1.
整理得2tx1-2y1+1=0.
设B(x2,y2),同理可得2tx2-2y2+1=0.
故直线AB的方程为2tx-2y+1=0.
所以直线AB过定点.
(2)解 由(1)得直线AB的方程为
y=tx+.
由可得x2-2tx-1=0.
于是x1+x2=2t,x1x2=-1,
y1+y2=t(x1+x2)+1=2t2+1,
|AB|=|x1-x2|
=×=2(t2+1).
设d1,d2分别为点D,E到直线AB的距离,
则d1=,d2=.
因此,四边形ADBE的面积
S=|AB|(d1+d2)=(t2+3).
设M为线段AB的中点,则M.
因为⊥,而=(t,t2-2),与向量(1,t)平行,
所以t+(t2-2)t=0,解得t=0或t=±1.
当t=0时,S=3;当t=±1时,S=4.
因此,四边形ADBE的面积为3或4.
新高考数学一轮复习课时过关练习第08章 平面解析几何第7节 直线与椭圆、双曲线 (含解析): 这是一份新高考数学一轮复习课时过关练习第08章 平面解析几何第7节 直线与椭圆、双曲线 (含解析),共18页。试卷主要包含了设双曲线C,过双曲线C,已知F1,F2为椭圆C等内容,欢迎下载使用。
新高考数学一轮复习课时过关练习第08章 平面解析几何第6节 双曲线 (含解析): 这是一份新高考数学一轮复习课时过关练习第08章 平面解析几何第6节 双曲线 (含解析),共24页。试卷主要包含了双曲线的标准方程和几何性质,双曲线的焦点到渐近线的距离为b,焦点三角形的面积,已知双曲线C等内容,欢迎下载使用。
新高考数学一轮复习课时过关练习第08章 平面解析几何第6节 双曲线 (含解析): 这是一份新高考数学一轮复习课时过关练习第08章 平面解析几何第6节 双曲线 (含解析),共24页。试卷主要包含了双曲线的标准方程和几何性质,双曲线的焦点到渐近线的距离为b,焦点三角形的面积,已知双曲线C等内容,欢迎下载使用。












