




高考数学一轮总复习课件第2章函数导数及其应用第4讲幂函数与二次函数(含解析)
展开一般地,形如 y=xα的函数称为幂函数,其中 x 是自变
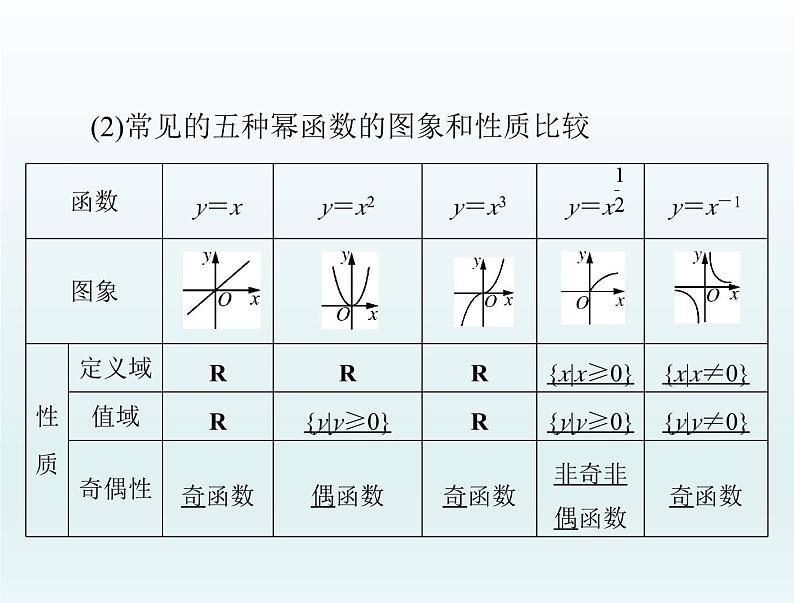
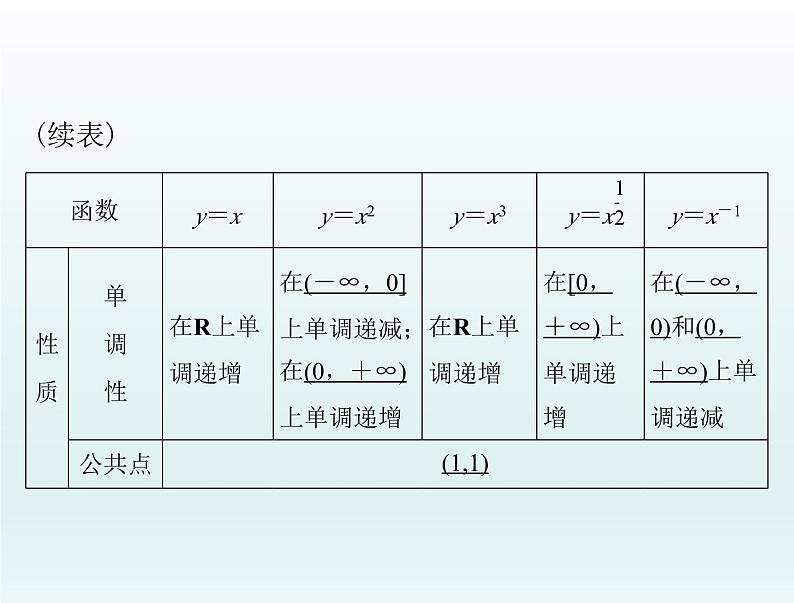
(2)常见的五种幂函数的图象和性质比较
【名师点睛】巧记幂函数 y=xα的图象
五个幂函数在第一象限内的图象的大致情况可以归纳为“正抛负双,大竖小横”,即α>0(α≠1)时的图象是抛物线型(α>1 时的图象是竖直抛物线型,0<α<1 时的图象是横卧抛物线型),α<0 时的图象是双曲线型.
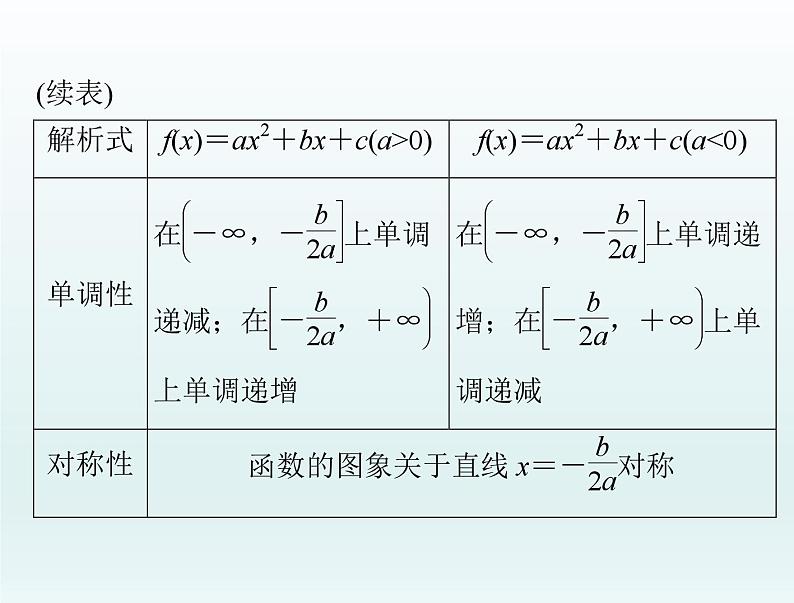
2.二次函数的图象和性质
(1)注意二次项系数对函数性质的影响,经常分二次项
系数大于零与小于零两种情况讨论.(2)一元二次不等式恒成立的条件
①“ax2+bx+c>0(a≠0)恒成立”的充要条件是“a
②“ax2+bx+c<0(a≠0)恒成立”的充要条件是“a
1.(多选题)下列结论中错误的是(
A.y=x0的图象是一条直线B.若幂函数y=xn是奇函数,则y=xn是增函数C.二次函数y=ax2+bx+c(x∈R)不可能是奇函数D.当n<0时,幂函数y=xn是定义域上的减函数
3.(教材改编题)函数f(x)=x2 -2x+3 在闭区间[0,3]上
的最大值为________,最小值为________.
考点一 幂函数的图象和性质
3.已知幂函数f(x)=(n2+2n-2)x (n∈Z)的图象关于 y 轴对称,且在(0,+∞)上单调递减,则 n 的值为
解析:由于 f(x)为幂函数,所以 n2+2n-2=1,解得n=1 或 n=-3,经检验只有 n=1 符合题意.故选 B.答案:B
(1)幂函数的形式是 y=xα(α∈R),其中只有一个参数α,
因此只需一个条件即可确定其解析式.
(2)在区间(0,1)上,幂函数中指数越大,函数图象越靠近 x 轴(简记为“指大图低”),在区间(1,+∞)上,幂函数中指数越大,函数图象越远离 x 轴.
(3)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较,准确掌握各个幂函数的图象和性质是解题的关键.
考点二 二次函数的图象与性质
考向 1 二次函数的图象
通性通法:抛物线的开口方向、对称轴位置、定义区
间三者相互制约,要注意分类讨论.
[例 1]如图 2-4-2 所示是二次函数 y=ax2+bx+c(a≠0)图象的一部分,图象过点 A(-3,0),对称轴为 x=-1.给出下面四个结论:图 2-4-2①b2>4ac;②2a-b=1;③a-b+c=0;④5a<b.
解析:结合题中图象可知该函数的图象与 x 轴交于两点,所以 b2-4ac>0,即 b2>4ac,①正确;又对称轴为
x=-1 时,y>0,即 a-b+c>0,③错误;由对称轴为x=-1 知,b=2a,又函数图象开口向下,所以 a<0,所以 5a<2a,即 5a<b,④正确.
考向 2 二次函数的单调性
通性通法:处理数学中的问题要注意数形结合思想的应用,尤其是给定区间上的二次函数最值问题,先“定性”(作草图),再“定量”(看图求解).
[例 2](多选题)若函数 f(x)=(x-1)|x+a|在区间(1,2)上
单调递增,则满足条件的实数 a 的值可能是(
解析:根据题意可知 f(x)=
考向 3 二次函数中的恒成立问题
通性通法:由不等式恒成立求参数取值范围的关键解题思路,一是分离参数;二是不分离参数.两种思路都是将问题归结为求函数的最值或值域.
[例 3]已知函数 f(x)=x2-x+1,在区间[-1,1]上不等
式 f(x)>2x+m 恒成立,求实数 m 的取值范围.
解:由题意可知,f(x)>2x+m 等价于 x2-x+1>2x+
m,即x2-3x+1-m>0,令g(x)=x2-3x+1-m,要使g(x)>0在[-1,1]上恒成立,只需使函数g(x)在[-1,1]上的最小值大于0即可.∵g(x)=x2-3x+1-m在[-1,1]上单调递减,∴g(x)min=g(1)=-m-1,由-m-1>0得m<-1.因此,满足条件的实数m的取值范围是(-∞,-1).
【考法全练】1.(考向 2)已知二次函数 f(x)满足 f(2+x)=f(2-x),且f(x)在[0,2]上单调递增,若 f(a)≥f(0),则实数 a 的取值范围
)A.[0,+∞)B.(-∞,0]C.(-∞,0]∪[4,+∞)D.[0,4]
解析:∵f(x)满足 f(2+x)=f(2-x),∴对称轴是 x=2,又 f(x)在[0,2]上单调递增,则抛物线的开口向下,且 f(x)在[2,4]上单调递减,∵f(a)≥f(0),则 f(a)≥f(4),所以根据二次函数的单调性并结合图象可得 0≤a≤4.故选 D.
2.(2021 年历下月考)已知函数 f(x)=-x2+ax+b(a,b∈R)的图象顶点的纵坐标为 0,若关于 a 的不等式 f(x)>c-1 的解集为(m-4,m),则实数 c 的值为________.
3.(考向 3)已知 a 是实数,函数 f(x)=2ax2+2x-3 在x∈[-1,1]上恒小于零,则实数 a 的取值范围为________.
⊙分类讨论思想在二次函数最值问题中的应用
[例 4]已知函数 f(x)=ax2+2ax+1 在区间[-1,2]上有最
大值 4,求实数 a 的值.解:f(x)=a(x+1)2+1-a.
①当 a=0 时,函数 f(x)在区间[-1,2]上的值为常数 1,
二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.无论哪种类型,解题的关键都是图象的对称轴与区间的位置关系,当含有参数时,要依据图象的对称轴与区间的位置关系进行分类讨论.
设函数 f(x)=x2-2x+2,x∈[t,t+1],t∈R,求函数
解:f(x)=x2-2x+2=(x-1)2+1,x∈[t,t+1],t∈R,
函数图象的对称轴为 x=1.
当 t+1≤1,即 t≤0 时,函数图象如图 D4(1)所示,函
数 f(x)在区间[t,t+1]上单调递减,
所以最小值为 f(t+1)=t2+1;
图 D4当 t<1
新高考数学一轮复习讲练测课件第2章§2.6二次函数与幂函数 (含解析): 这是一份新高考数学一轮复习讲练测课件第2章§2.6二次函数与幂函数 (含解析),共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,y=xα,奇函数,偶函数,即p0,解得a=-4,当a0时,fx=x2-等内容,欢迎下载使用。
高考数学一轮总复习课件第2章函数导数及其应用第7讲函数的图象(含解析): 这是一份高考数学一轮总复习课件第2章函数导数及其应用第7讲函数的图象(含解析),共50页。PPT课件主要包含了描点法作图,2对称变换,3伸缩变换,4翻折变换,名师点睛,中心对称,的图象相同,答案A,答案C,题组三真题展现等内容,欢迎下载使用。
2024版高考数学一轮总复习第2章函数第4节二次函数与幂函数课件: 这是一份2024版高考数学一轮总复习第2章函数第4节二次函数与幂函数课件,共46页。












