





高考数学一轮总复习课件第2章函数导数及其应用第6讲对数与对数函数(含解析)
展开一般地,如果 ax=N(a>0,且 a≠1),那么数 x 叫做以a 为底 N 的对数,记作 x=lgaN,其中 a 叫做对数的底数,N 叫做真数.
2.对数的运算法则和性质(1)对数的运算法则
如果 a>0,且 a≠1,M>0,N>0,那么:
(2)对数的性质①负数和零没有对数.②lga1=0,lgaa=1(a>0,且 a≠1).④lgaaN=N(a>0,且 a≠1).(3)对数的换底公式
【名师点睛】对数运算的一些结论
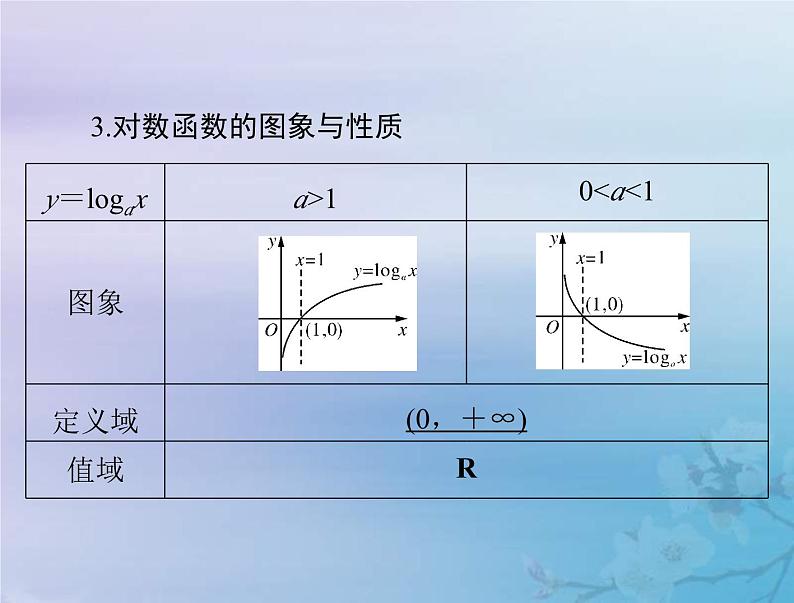
3.对数函数的图象与性质
指数函数y=ax(a>0且a≠1)与对数函数y=lgax(a>0且 a≠1)互为反函数,它们的图象关于直线 y=x对称.
(1) 对数函数的图象与底数大小的比较如图 2-6-1 所示,作直线 y=1,则该直线与四个函数图象交点的横坐标为相应的底数.
故 0<c<d<1<a<b.
由此我们可得到以下规律:在第一象限内从左到右底
(2)对数不等式问题,一般是先确保对数中真数大于 0,再利用对数函数的单调性来求解不等式,特别是对数函数的底数不确定时,单调性不明确,从而无法求解不等式,故应分 a>1 和 0
题组二 走进教材2.(教材改编题)若 lg 2=a,lg 3=b,则 lg 12 的值为
)B.c<a<bD.a<c<b
则 a,b,c 的大小关系为(A.a<b<cC.b<c<a答案:D
)B.b<a<cD.a<b<c
则 a,b,c 的大小关系为(A.c<b<aC.a<c<b答案:C
1.(多选题)若2x=3,3y=4,则下列选项正确的是( )
【题后反思】对数运算的一般思路
(1)拆:首先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后利用对数运算性质化简合并.
(2)合:将对数式化为同底数的和、差、倍数运算,然后逆用对数的运算性质,转化为同底对数真数的积、商、幂的运算.
考点二 对数函数的图象及应用a>0,且 a≠1,则函数 f(x),g(x)在同一坐标系中的大致图
[例1](1)(多选题)若函数f(x)=ax-2,g(x)=lga|x|,其中
解析:易知 g(x)=lga|x|为偶函数.当 0<a<1 时,f(x)
=ax-2单调递减,g(x)=lga|x|在(0,+∞)上单调递减,此时A选项符合题意;当a>1时,f(x)=ax-2单调递增,g(x)=lga|x|在(0,+∞)上单调递增,此时D选项符合题意.故选AD.
【题后反思】利用对数函数的图象解决的两类问题及
(1)对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想.
(2)一些对数型方程、不等式问题常转化为相应的函数
图象问题,利用数形结合法求解.
【变式训练】1.已知函数 f(x)是定义在 R 上的偶函数,且当 x≥0 时,
f(x)=ln(x+1),则函数 f(x)的大致图象为(
解析:先作出当 x≥0 时,f(x)=ln(x+1)的图象(图略),显然图象经过点(0,0),再作此图象关于 y 轴对称的图象,可得函数 f(x)在 R 上的大致图象,如 C 中图象所示.故选 C.
f(x)+x-a=0 有且只有一个实根,则实数 a 的取值范围是________.
解析:问题等价于函数 y=f(x)与 y=-x+a 的图象有
且只有一个交点,结合图 D6 可知 a>1.
考点三 对数函数的性质及应用考向 1 解对数方程、不等式
通性通法:求解对数不等式的两种类型及方法
[例 2](1)方程lg2(x-1)=2-lg2(x+1)的解为______.
考向 2 比较指数式、对数式的大小通性通法:比较对数值大小的方法
A.a<b<cC.a<c<b
B.b<a<cD.b<c<a
因此 b<a<c.答案:B
(2)(2020 年全国Ⅲ)已知55<84,134<85.设a=lg53,b=
lg85,c=lg138,则( A.a
通性通法:对数型复合函数的单调性问题的求解策略(1)对于 y=lgaf(x)型的复合函数的单调性,有以下结论:函数 y=lgaf(x)的单调性与函数 u=f(x)[f(x)>0]的单调性在 a>1 时相同,在 0
[例 4](1)(2020 年新高考Ⅱ)已知函数 f(x)=lg(x2-4x-
5)在(a,+∞)单调递增,则 a 的取值范围是(
A.(-∞,-1]C.[2,+∞)
B.(-∞,2]D.[5,+∞)
解析:由 x2-4x-5>0,得 x<-1 或 x>5,即函数
f(x)的定义域为(-∞,-1)∪(5,+∞).令t=x2-4x-5,则t=(x-2)2-9,所以函数t在(-∞,-1)上单调递减,在(5,+∞)上单调递增,又函数y=lg t在(0,+∞)上单调递增,从而函数f(x)的单调递增区间为(5,+∞),由题意知(a,+∞)⊆(5,+∞),∴a≥5.
【考法全练】1.(考向 2)(多选题)(2021 年胶州期末)已知 a=30.1,b=
lg0.93,c=sin(cs 1),则下述正确的是(
解析:a=30.1>1,b=lg0.93<0,c=sin(cs 1)∈(0,1),则 a>c>b.故选 AB.答案:AB
2.(考向 3)若函数f(x)=lg2(x2-ax-3a)在区间(-∞,
-2]上单调递减,则实数 a 的取值范围是(A.(-∞,4)B.(-4,4]C.(-∞,-4)∪[-2,+∞)D.[-4,4)
解析:由 x2-3x+2>0 得 x>2 或 x<1,即函数的定
义域为{x|x>2 或 x<1},
当 x 在定义域内变化时,x2-3x+2 取遍(0,+∞)内的
每一个值,∴值域为 R.
答案:(-∞,1) R
4.(考向 3)若函数f(x)=lga(x2-x+2)在区间[0,2]上的最大值为 2,则实数 a=________.
⊙数形结合探讨对数函数的性质
解析:正实数 m,n 满足 m
f(m)=|lg2m|=f(n)=|lg2n|,-lg2m=lg2n,
解析:作出 f(x)的大致图象如图 D7,
由图象知,要使 f(a)=f(b)=f(c),不妨设 a
高考数学一轮总复习课件第2章函数导数及其应用第八讲函数与方程(含解析): 这是一份高考数学一轮总复习课件第2章函数导数及其应用第八讲函数与方程(含解析),共44页。PPT课件主要包含了答案B,图2-8-3,答案12,图D12,图D13,答案3,个解就有几个零点,答案D,图2-8-4,答案1等内容,欢迎下载使用。
高考数学一轮总复习课件第2章函数导数及其应用第7讲函数的图象(含解析): 这是一份高考数学一轮总复习课件第2章函数导数及其应用第7讲函数的图象(含解析),共50页。PPT课件主要包含了描点法作图,2对称变换,3伸缩变换,4翻折变换,名师点睛,中心对称,的图象相同,答案A,答案C,题组三真题展现等内容,欢迎下载使用。
高考数学一轮总复习课件第2章函数导数及其应用第5讲指数与指数函数(含解析): 这是一份高考数学一轮总复习课件第2章函数导数及其应用第5讲指数与指数函数(含解析),共52页。PPT课件主要包含了答案ABCD,答案B,答案C,答案A,图2-5-2,答案02,题后反思,答案D,图D5,答案01等内容,欢迎下载使用。












