高考数学一轮总复习课件第2章函数导数及其应用第7讲函数的图象（含解析）

这是一份高考数学一轮总复习课件第2章函数导数及其应用第7讲函数的图象（含解析），共50页。PPT课件主要包含了描点法作图，2对称变换，3伸缩变换，4翻折变换，名师点睛，中心对称，的图象相同，答案A，答案C，题组三真题展现等内容，欢迎下载使用。

方法步骤：(1)确定函数的定义域；(2)化简函数的解析式；(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势)；(4)描点连线，画出函数的图象.
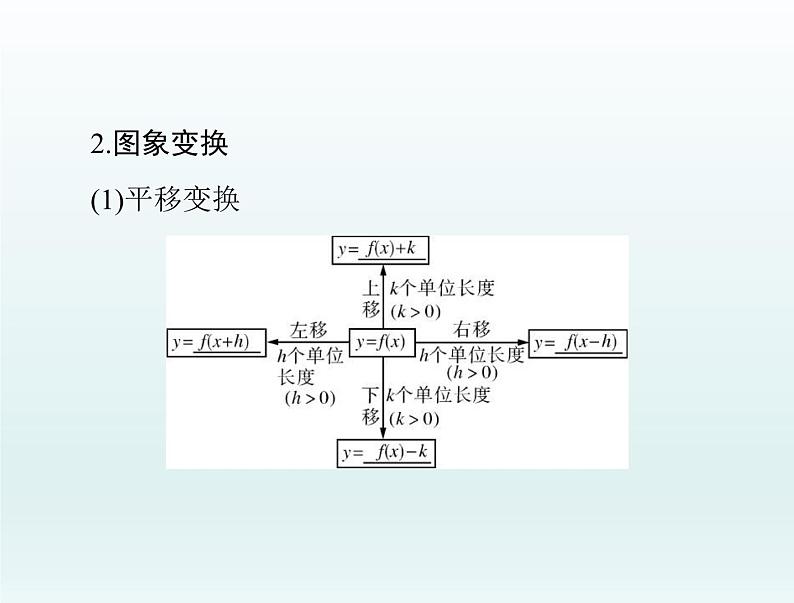
2.图象变换(1)平移变换
①y＝f(x)②y＝f(x)③y＝f(x)
y＝－f(x).y＝f(－x).y＝－f(－x).
y ＝ lgax(a>0 且
④ y ＝ ax (a>0 且 a≠1)a≠1).
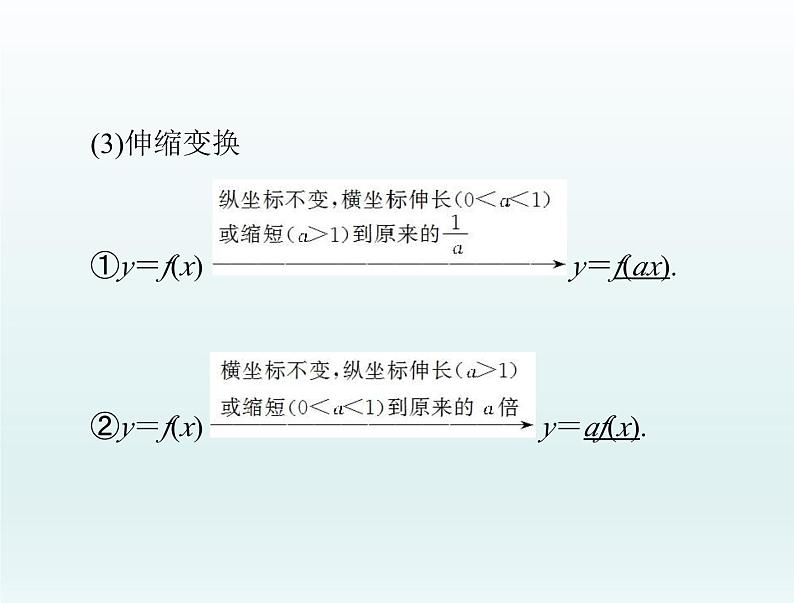
①y＝f(x)②y＝f(x)
y＝f(ax).y＝af(x).
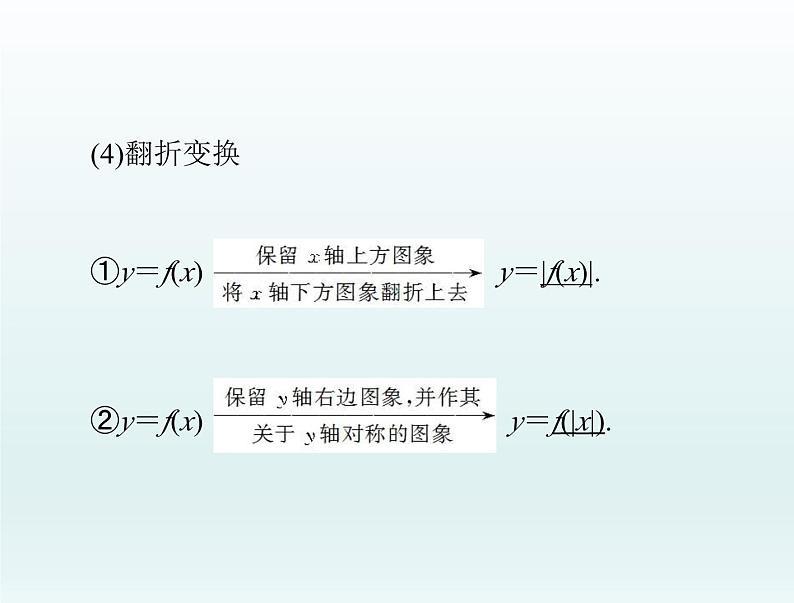
y＝|f(x)|.y＝f(|x|).
(1)函数 y＝f(x)与 y＝f(2a－x)的图象关于直线 x＝a 对
(2)函数 y＝f(x)与 y＝2b－f(2a－x)的图象关于点(a，b)
(3)若函数 y＝f(x)对定义域内任意自变量 x 满足：f(a＋x)＝f(a－x)，则函数 y＝f(x)的图象关于直线 x＝a 对称.
题组一 走出误区1.判断下列结论正误(在括号内打“√”或“×”)(1)函数 y＝f(1－x)的图象，可由 y＝f(－x)的图象向左
平移 1 个单位长度得到.(
(2)函数 y＝f(x)的图象关于 y 轴对称即函数 y＝f(x)与
y＝f(－x)的图象关于 y 轴对称.(
(3)当 x∈(0，＋∞)时，函数 y＝f(|x|)的图象与 y＝|f(x)|
(4)若函数 y＝f(x)满足 f(1＋x)＝f(1－x)，则函数 f(x)的
图象关于直线 x＝1 对称.(
答案：(1)× 　(2)×　 (3)×　 (4)√
题组二 走进教材2.(教材改编题)函数f(x)＝ln(x2＋1)的图象大致是
考点一 作函数的图象[例 1]分别作出下列函数的图象：
解：(1)首先作出 y＝lg x 的图象，然后将其向右平移 1个单位长度，得到 y＝lg(x－1)的图象，再把所得图象在 x轴下方的部分翻折到 x 轴上方，即得所求函数 y＝|lg(x－1)|的图象，如图 2-7-2 所示(实线部分).
(2)将y＝2x的图象向左平移1个单位长度，得到y＝2x＋1的图象，再将所得图象向下平移1个单位长度，得到y＝2x＋1－1的图象，如图2­7­3所示.
例函数、指数函数、对数函数、幂函数、形如y＝x＋ 的
【题后反思】图象变换法作函数的图象
(1)熟练掌握几种初等函数的图象，如二次函数、反比
(2)若函数图象可由某个基本初等函数的图象经过平移、翻折、对称或伸缩得到，可利用图象变换作出，但要注意变换顺序.
分别作出下列函数的图象：(1)y＝|lg x|；(2)y＝sin |x|.
解：(1)先作出函数 y＝lg x 的图象，再将 x 轴下方的部分沿 x 轴翻折上去，即可得函数 y＝|lg x|的图象，如图 D9①实线部分.
图 D9(2)当 x≥0 时，y＝sin |x|与 y＝sin x 的图象完全相同，又 y＝sin |x|为偶函数，图象关于 y 轴对称，其图象如图 D9②.
考点二 函数图象的辨识
y>0，排除 A；当 x＝π时，y＝1＋π，排除 B，D 满足.(法二)当 x＝1 时，f(1)＝1＋1＋sin 1＝2＋sin 1>2，排除 A，C；又当 x→＋∞时，y→＋∞，排除 B，D 满足.
(2)函数y＝2x2－e|x|在[－2,2]的图象大致为(　　)
解析：f(x)＝2x2－e|x|，x∈[－2,2]是偶函数，
又f(2)＝8－e2∈(0,1)，排除A，B；当x≥0时，f(x)＝2x2－ex，f′(x)＝4x－ex，所以f′(0)＝－1<0，f′(2)＝8－e2>0，所以函数f′(x)在(0,2)上有解，故函数f(x)在[0,2]上不单调，排除C，故选D.
【题后反思】函数图象的识别方法
(1)特殊点法：根据已知函数的解析式选取特殊的点，判断选项中的图象是否经过这些点，若不满足则排除.(2)函数性质法：根据选项中的图象特点，结合函数的奇偶性、单调性等来排除选项，有时需要借助导数工具求解.
(3)极限思想：应用极限思想来处理，达到巧解妙算的
效果，使解题过程费时少，准确率高.
(4)图象变换法：有关函数 y＝f(x)与函数 y＝af(bx＋c)＋h 的图象问题的判断，熟练掌握图象的平移变换(左加右减，上加下减)、对称变换、伸缩变换等，便可破解此类问题.
2.(2021 年南开模拟)已知函数 f(x)的图象如图 2-7-6 所
示，则函数 f(x)的解析式可能是(图 2-7-6
A.f(x)＝(4x－4－x)|x|　　　B.f(x)＝(4x－4－x)lg2|x|C.f(x)＝(4x＋4－x)|x|　　　D.f(x)＝(4x＋4－x)lg2|x|
解析：对于A，f(x)＝(4x－4－x)|x|，其定义域为R，有
f(－x)＝(4－x－4x)|x|＝－f(x)，则函数f(x)为奇函数，不符合题意；对于B，f(x)＝(4x－4－x)lg2|x|，其定义域为{x|x≠0}，有f(－x)＝(4－x－4x)lg2|x|＝－f(x)，则函数f(x)为奇函数，不符合题意；对于C，f(x)＝(4x＋4－x)|x|，在区间(0,1)上，f(x)＞0，不符合题意.故选D.
考点三 函数图象的应用考向 1 研究函数的性质
通性通法：利用函数的图象研究函数的性质对于已知或易画出其在给定区间上图象的函数，其性质[单调性、奇偶性、周期性、最值(值域)、零点]常借助于图象研究，但一定要注意性质与图象特征的对应关系.
[例 3]已知函数 f(x)＝x|x|－2x，则下列结论正确的是
)A.f(x)是偶函数，递增区间是(0，＋∞)B.f(x)是偶函数，递减区间是(－∞，1)C.f(x)是奇函数，递减区间是(－1,1)D.f(x)是奇函数，递增区间是(－∞，0)
解析：将函数 f(x)＝x|x|－2x 去掉绝对值得
画出函数 f(x)的图象，如图 2-7-7，观察图象可知，函数 f(x)的图象关于原点对称，故
函数 f(x)为奇函数，且在(－1,1)上是减少的.
考向 2 求不等式的解集
通性通法：当不等式问题不能用代数法求解或用代数法求解比较困难，但其对应函数的图象可作出时，常将不等式问题转化为两函数图象的位置关系问题，从而利用数形结合思想求解.
[例 4]已知函数 y＝f(x)的图象是如图 2-7-8 所示的折线ACB，且函数 g(x)＝lg2(x＋1)，则不等式 f(x)≥g(x)的解集
A.{x|－1B.{x|－1≤x≤1}D.{x|－1解析：令 y＝g(x)＝lg2(x＋1)，作出函数 g(x)图象如图 2-7-9，
∴结合图象知不等式 f(x)≥lg2(x＋1)的解集为{x|－1A.(－1,0)∪(1，＋∞)B.(－∞，－1)∪(0,1)C.(－∞，－1)∪(1，＋∞)D.(－1,0)∪(0,1)
2.(考向 1)(2021 年贵阳模拟)已知函数 f(x)的图象如图2-7-10 所示，则函数 g(x)＝lg f(x)的定义域是________.
解析：当 f(x)＞0 时，函数 g(x)＝lg f(x)有意义，由
函数 f(x)的图象知满足 f(x)＞0 的 x∈(2,8].
⊙由实际问题的变化过程探究函数图象[例 5]广为人知的太极图，其形状如阴阳两鱼互纠在一起，因而被习称为“阴阳鱼太极图”.如图 2-7-11，是由一个半径为 2 的大圆和两个半径为 1 的半圆弧组成的“阴阳鱼太极图”，圆心分别为 O，O1，O2，若一动点 P 从点 A出发，按路线 A→O→B→C→A→D→B 运动(其中 A，O1，O，O2，B 五点共线)，设 P 的运动路程为 x，y＝|O1P|2，y
与 x 的函数关系式为 y＝f(x)，则 y＝f(x)的图象大致为(
解决此类问题，可以根据已知条件求出函数解析式后再判断函数的图象；也可采用“以静观动”，即将动点处于某些特殊的位置处考查图象的变化特征，从而得出结果.
【高分训练】1.如图 2-7-12，已知 l1⊥l2，点 O 在 l1 上，半径为 1 m的圆 O 在 t＝0 时与 l2 相切于点 A，圆 O 沿 l1 以 1 m/s 的速度匀速向上移动，直线 l2 被圆 O 截得的上方圆弧长记为 x，令 y＝cs x，则 y 与时间 t(0≤t≤1，单位：s)的函数 y＝f(t)
解析：如图 D11，设直线 l2 与圆 O 交于 M，N 两点，∠MON＝α，由弧长公式知 x＝α，在 Rt△AOM 中，|AO|
2.(2021 年番禺期末)音乐是用声音来表达人的思想感情的一种艺术.声音的本质是声波，而声波在空气中的振动可以用三角函数来刻画.在音乐中可以用正弦函数来表示单音，用正弦函数相叠加表示和弦.某二和弦可表示为 f(x)
＝sin 2x＋sin 3x，则函数 y＝f(x)的图象大致为(