高考数学一轮总复习课件第5章平面向量与复数第3讲平面向量的数量积（含解析）

这是一份高考数学一轮总复习课件第5章平面向量与复数第3讲平面向量的数量积（含解析），共56页。PPT课件主要包含了向量的夹角，平面向量的数量积，题组一走出误区，答案ACD，题组二走进教材，答案C，题组三真题展现，答案03，图5-3-1，图5-3-2等内容，欢迎下载使用。
3.平面向量数量积的运算律(1)交换律：a·b＝b·a.
(2)数乘结合律：(λa)·b＝λ(a·b)＝a·(λb).(3)分配律：a·(b＋c)＝a·b＋a·c.
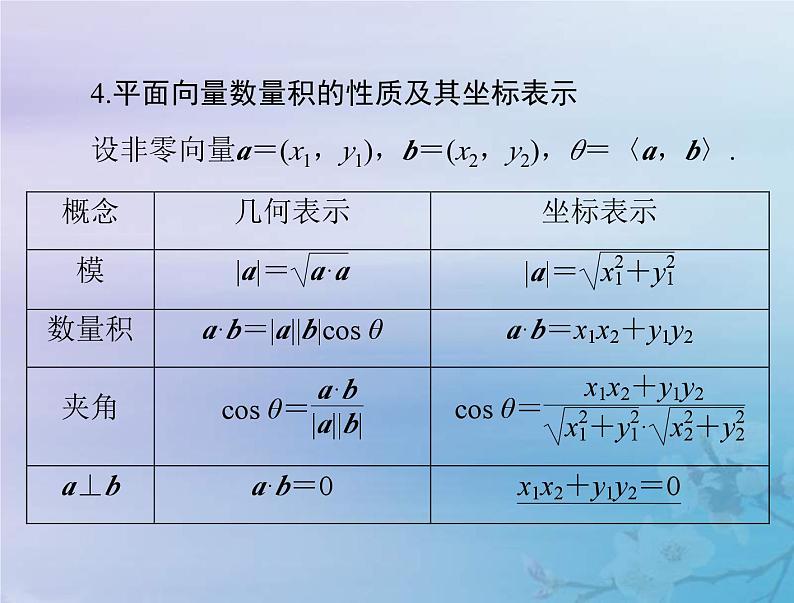
4.平面向量数量积的性质及其坐标表示
设非零向量a＝(x1，y1)，b＝(x2，y2)，θ＝〈a，b〉.
提醒：a∥b与a⊥b所满足的坐标关系不同.a∥b⇔x1y2
＝x2y1；a⊥b⇔x1x2＋y1y2＝0.
【名师点睛】(1)平面向量数量积运算的常用公式①(a＋b)·(a－b)＝a2－b2.②(a±b)2＝a2±2a·b＋b2.(2)两个向量 a，b 的夹角为锐角⇔a·b＞0 且 a，b 不共线；两个向量 a，b 的夹角为钝角⇔a·b＜0 且 a，b 不共线.
1.(多选题)下列命题中正确的是(
A.非零向量 a，b 满足|a|＝|b|＝|a－b|，则 a 与 a＋b 的夹角为 30°B.若 a·b＞0，则 a，b 的夹角为锐角
3.(教材改编题)已知向量 a＝(2,2)，b＝(－8,6)，则cs〈a，b〉＝________.
4.(2021 年北京)已知 a＝(2,1)，b＝(2，－1)，c＝(0,1)，
则(a＋b)·c＝________；a·b＝________.
5.(2020 年全国Ⅰ)设 a，b 为单位向量，且|a＋b|＝1，
则|a－b|＝________.
考点一 平面向量数量积的基本运算
[例 1]如图5­3­1，在梯形ABCD中，AB∥CD，CD＝2，
解析：法一(几何法)：
法二(坐标法)：如图 5-3-2，建立平面直角坐标系 xAy.依题意，可设点 D(m，m)，C(m＋2，
m)，B(n,0)，其中 m>0，n>0，
【题后反思】平面向量数量积的三种运算方法
(1)当已知向量的模和夹角时，可利用定义法求解，即
a·b＝|a||b|cs〈a，b〉.
(2)当已知向量的坐标时，可利用坐标法求解，即若
a＝(x1，y1)，b＝(x2，y2)，则a·b＝x1x2＋y1y2.
(3)利用数量积的几何意义求解.
解析：如图 D27 所示，设 AC 的中点为 E，AB 的中点为 F，连接 OA，OF，OD，OE，图 D27
解析：以 A 为坐标原点，AB 所在直线为 x 轴，AD 所在直线为 y 轴，建立平面直角坐标系，如图 D28 所示，则 B(2,0)，C(1,1)，D(0,1)，
考点二 平面向量数量积的应用
考向 1 求向量的模
通性通法： 求解平面向量模的方法
考向 2 求向量的夹角通性通法：求平面向量的夹角的方法
(3)解三角形法：把两向量的夹角放到三角形中.
[例 3](1)已知非零向量 a，b 满足|a|＝2|b|，且(a－b)⊥b，
则 a 与 b 的夹角为(
(2)若向量 a＝(k,3)，b＝(1,4)，c＝(2,1)，已知 2a－3b与 c 的夹角为钝角，则 k 的取值范围是________.
考向 3 两个向量垂直问题
通性通法：(1)利用坐标运算证明两个向量的垂直问题若证明两个向量垂直，先根据共线、夹角等条件计算出这两个向量的坐标；然后根据数量积的坐标运算公式，计算出这两个向量的数量积为 0 即可.
(2)已知两个向量的垂直关系，求解相关参数的值根据两个向量垂直的充要条件，列出相应的关系式，
[例 4](1)(2020 年全国Ⅱ)已知单位向量 a，b 的夹角为
60°，则在下列向量中，与 b 垂直的是(
A.a＋2bC.a－2b
B.2a＋bD.2a－b
2.(考向 2)(多选题)(2021 年城厢模拟)已知向量 a＝(λ，
1)，b＝(1，－2)，记向量 a，b 的夹角为θ，则(A.λ＞2 时，θ为锐角B.λ＜2 时，θ为钝角C.λ＝2 时，θ为直角
∵(c－a)·(c－b)＝－1，
∴x2＋y2－6x－2y＋9＝0，即(x－3)2＋(y－1)2＝1，所以点 C 在以(3,1)为圆心，1 为半径的圆上，|c－a|表示点 A，C 的距离，即圆上的点与 A(4,0)的距离，因为圆心到 A 的
⊙数量积运算的最值或取值范围
解析：(法一，几何法)第一步：画出图形，利用向量
(法二，坐标法)第一步：建立平面直角坐标系.
以 BC 中点为坐标原点，建立如图 5-3-7 所示的坐标系，
【反思感悟】求解平面向量数量积最值或取值范围问
题的两个策略(1)图形化策略
所谓图形化策略，是指解决向量问题时，利用图形语言翻译已知条件和所求结论，借助图形思考解决问题.图形化策略体现了数形结合思想，同时，化归与转化思想和函数与方程思想也深蕴其中.
利用图形化的策略方法，各种数量关系在图形中非常明了，能起到事半功倍的作用.如果没有图形的帮助，要用代数化策略，这样即使是坐标化处理，也可能陷入“僵局”.
所谓代数化策略，是指解决向量问题时，利用代数语言翻译已知条件和所求结论，借助代数运算解决所面临的问题.代数化策略体现了化归与转化思想和函数与方程思想.通过平面向量基本定理演变而来的代数运算和坐标化的代数运算，是解决向量问题的一般方法.
A.[－1,8]C.[0,8]
B.[－1，＋∞)D.[－1,0]
解析：如图 D29，以 BC 的中点 O 为原点，OC，OA所在直线分别为 x 轴、y 轴建立平面直角坐标系 xOy，