






高考数学一轮总复习课件第8章统计与统计分析第3讲成对数据的统计分析(含解析)
展开(1)相关关系:当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系.与函数关系不同,相关关系是一种非确定性关系.
(2)散点图:表示具有相关关系的两个变量的一组数据的图形叫做散点图,它可直观地判断两变量的关系是否可以用线性关系表示.若这些散点有 y 随 x 增大而增大的趋势,则称两个变量正相关;若这些散点有 y 随 x 增大而减小的趋势,则称两个变量负相关.
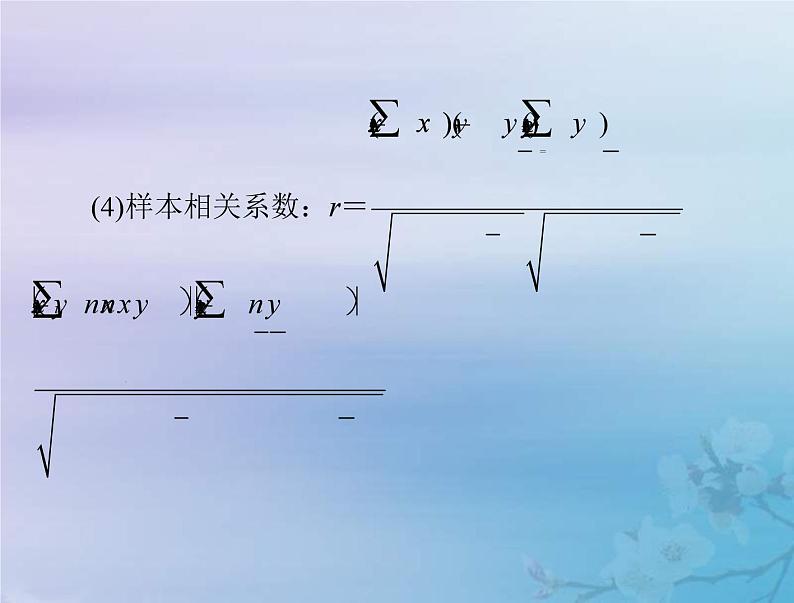
它主要用于相关量的显著性检验,以衡量它们之间的线性相关程度.当 r>0 时表示两个变量正相关,当 r<0 时表示两个变量负相关.|r|越接近 1,表明两个变量的线性相关性越强;当|r|接近 0 时,表明两个变量间几乎不存在相关关系,相关性越弱.
设 X,Y 为两个分类变量,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(2×2 列联表)如下:
a+b+c+d 为样本容量)来判断“两个变量有关系”的方法称为独立性检验.
(3)独立性检验的一般步骤①根据样本数据列出2×2列联表;②计算随机变量χ2的值,查表确定临界值xα;③如果χ2≥xα,就推断“X与Y有关系”,这种推断犯错误的概率不超过P(χ2≥xα);否则,就认为在犯错误的概率不超过P(χ2≥xα)的前提下不能推断“X与Y有关系”.
(1)回归分析是对具有相关关系的两个变量进行统计分析的方法,只有在散点图大致呈线性分布时,求出的线性回归方程才有实际意义,否则,求出的线性回归方程毫无意义.根据回归方程进行预报,仅是一个预报值,而不是真实发生的值.
(2)独立性检验是对两个变量的关系的可信程度的判断,而不是对其是否有关系的判断.根据χ2 的值可以判断两个分类变量有关的可信程度,并用来指导科研和实际生活.
1.判断下列结论正误(在括号内打“√”或“×”)(1)“名师出高徒”可以解释为教师的教学水平与学
生的水平成正相关关系.(
(3)因为由任何一组观测值都可以求得一个线性回归
方程,所以没有必要进行相关性检验.(
(4)事件 X,Y 关系越密切,则由观测数据计算得到的
χ2 的观测值越大.(
2.(教材改编题)为调查中学生近视情况,测得某校 150名男生中有 80 名近视,140 名女生中有 70 名近视.在检验这些学生眼睛近视是否与性别有关时,用下列哪种方法最
B.均值与方差D.概率
A.回归分析C.独立性检验答案:C
3.(教材改编题)两个变量 y 与 x 的回归模型中,分别选择了 4 个不同模型,它们的相关指数 R2 如下,其中拟合效
A.模型 1 的相关指数 R2 为 0.98B.模型 2 的相关指数 R2 为 0.80C.模型 3 的相关指数 R2 为 0.50D.模型 4 的相关指数 R2 为 0.25答案:A
4.(2020 年全国Ⅰ)某校一个课外学习小组为研究某作物种子的发芽率 y 和温度 x(单位:℃)的关系,在 20 个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到散点图(如图 8-3-1):图 8-3-1
由此散点图,在 10 ℃至 40 ℃之间,下面四个回归方程类型中最适宜作为发芽率 y 和温度 x 的回归方程类型的
B.y=a+bx2D.y=a+bln x
A.y=a+bxC.y=a+bex答案:D
考点一1.观察下列各图形,
其中两个变量 x,y 具有相关关系的图是(
解析:由散点图知③中的点都分布在一条直线附近.④中的点都分布在一条曲线附近,所以③④中的两个变量具有相关关系.故选 C.
2.(多选题)关于回归分析,下列说法正确的是(
A.在回归分析中,变量间的关系若是非确定性关系,那么因变量不能由自变量唯一确定B.线性相关系数可以是正的也可以是负的C.在回归分析中,如果 r2=1 或 r=±1,说明 x 与 y 之间完全线性相关D.样本相关系数 r∈(-1,1)
解析:选项 D 中,样本相关系数应满足-1≤r≤1,
故 D 错误,ABC 都正确.故选 ABC.
3.x 和 y 的散点图如图 8-3-2 所示,则下列说法中正确
命题的序号有________.
解析:在散点图中,点散布在从左上角到右下角的区域,因此 x,y 是负相关关系,故①正确;由散点图知用 y正确;x,y 之间可以建立线性回归方程,但拟合效果不好,故③错误.
[例 1](1)(多选题)某市物价部门对 5 家商场的某商品一天的销售量及其价格进行调查,5 家商场的售价 x(元)和销售量 y(件)之间的一组数据如表所示:
(2)某农科所实地考察,研究发现某贫困村适合种植两种药材,可以通过种植这两种药材脱贫,通过大量考察研究得知药材 A 的亩产量约为 300 kg,其收购价格处于上涨趋势,最近五年的价格如下表:
药材 B 的收购价格始终为 20 元/kg,其亩产量的频率
分布直方图如图 8-3-3,
(1)若药材 A 的单价 y(单位:元/kg)与年份编号 x 具有线性相关关系,请求出 y 关于 x 的回归直线方程,并估计2023 年药材 A 的单价;(2)用上述频率分布直方图估计药材 B 的平均亩产量,若不考虑其他因素,试判断 2023 年该村应种植药材 A 还是药材 B?并说明理由.
(2)由(1)知,2023 年种植药材 A 的收入为 39.2×300=
由频率分布直方图可知,(360×0.005+380×0.01+400×0.017 5+420×0.012 5+440×0.005)×20=401,
∴药材 B 的平均亩产量为 401 kg,
∵药材 B 的收购价格始终为 20 元/kg,
∴2023 年种植药材 B 的收入为 20×401=8 020<
故 2023 年该村应种植药材 A.
【题后反思】回归分析问题的类型及解题方法(1)求经验回归方程
①根据散点图判断两变量是否线性相关,如不是,应
通过换元构造线性相关.
②利用公式,求出回归系数 .
③利用经验回归直线过样本点的中心求系数a.
(2)利用经验回归方程进行预测时,可把经验回归方程
看作一次函数求函数值.
(3)利用经验回归方程判断正、负相关时,决定是正相
关还是负相关的是系数 .
(4)判断经验回归方程的拟合效果,可以利用样本相关系数判断,|r|越趋近于 1,两变量的线性相关性越强.
某公司为确定下一年度投入某种产品的宣传费,需了解这种产品的年广告费支出 x(单位:万元)对年销售额 y(单位:万元)的影响,对近 5 年的年广告费支出 x 和年销售额y 进行统计,得到如下数据:
(1)请根据表中数据,建立 y 与 x 的经验回归方程;(2)当年广告费支出为 10 万元时,估计年销售额 y 的预报值是多少万元?附:回归方程中斜率和截距的最小-乘估计公式分别
(2)当 x=10 时, =6.5×10+17.5=82.5(万元),所以当年广告费支出为 10 万元时,估计年销售额 y
的预报值是 82.5 万元.
[例 2]电视传媒公司为了解某地区观众对“中国诗词大会”的收视情况,随机抽取了 100 名观众进行调查,其中女性有 55 名.将日均收看该节目时间不低于 40 分钟的观众称为“诗词迷”,已知“诗词迷”中有 15 名男性,“非诗词迷”共有 75 名.
(1)根据已知条件完成下面的 2×2 列联表,并据此资料判断是否有 95%的把握认为是否为“诗词迷”与性别有关?
(2)采用分层随机抽样的方式从“诗词迷”中任意选取 5 人进行问卷调查,若再从这 5 人中任意选取 2 人奖励诗词大礼包,求选取的 2 人为一位男性一位女性的概率.
解:(1)在抽取的 100 个人中,“非诗词迷”共有 75名,则“诗词迷”有 25 人,女性有 55 名,所以 2×2 列联表如下:
所以没有 95%的把握认为是否为“诗词迷”与性别有关.
新型冠状病毒的传染主要是人与人之间进行传播,感染人群年龄大多数是 50 岁以上人群.该病毒进入人体后有潜伏期,潜伏期是指病原体侵入人体至最早出现临床症状的这段时间,潜伏期越长,感染到他人的可能性越高,现对 400 个病例的潜伏期(单位:天)进行调查,如果认为超过 8 天的潜伏期属于“长潜伏期”,按照年龄统计样本,50 岁以上人数占 70%,长期潜伏人数占 25%,其中 50 岁以上长期潜伏者有 60 人.
(1)请根据以上数据完成 2×2 列联表;单位:人
(2)判断是否有 95% 的把握认为是否是“长期潜伏”者与年龄有关.
解:(1)根据题目所给数据得到如下 2×2 列联表,单
3.841,所以有 95%以上的把握认为是否是“长期潜伏者”与年龄有关.
⊙非线性回归的应用问题
[例 3]为了研究一种昆虫的产卵数 y(单位:个)和温度x(单位:℃)是否有关,现收集了 7 组观测数据列于下表中,并作出了如图 8-3-4 所示的散点图,发现样本点没有分布在某个带状区域内,两个变量不呈线性相关关系,现分别
和温度 x 的回归方程来建立两个变量之间的关系.
(1) 分别在图 8-3-5(1)(2)中画出 y 关于 t 的散点图和 z关于 x 的散点图,根据散点图判断哪一个模型更适合作为昆虫的产卵数 y 关于温度 x 的回归方程.(给出判断即可,不必说明理由)
解:(1)画出 y 关于 t 的散点图,如图 8-3-6 所示.
画出 z 关于 x 的散点图,如图 8-3-7 所示.
根据散点图可以判断模型②更适合作为昆虫的产卵数
y 关于温度 x 的回归方程类型.
【反思感悟】非线性回归方程的求法(1)根据原始数据作出散点图;
(2)根据散点图,选择恰当的拟合函数;
(3)作恰当变换,将其转化成线性函数,求线性回归方
(4)在(3)的基础上通过相应变换,即可得非线性回归方
1.(2021 年昌江期中)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 x(单位:千元)对年销售量y(单位:t)和年利润 z(单位:千元)的影响,对近 8 年的宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到散点图(如图 8-3-8)及一些统计量的值.
(1)根据散点图判断 y=a+bx 与 y=c+d ,哪一个适合作为年销售量 y 关于年宣传费 x 的回归方程类型;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立 y 关于 x 的回
(3)已知这种产品的年利润 z 与 x,y 的关系为 z=
0.2y-x,根据(2)的结果回答下列问题:
①当年宣传费 x=49 时,年销售量及年利润的预报值
②当年宣传费 x 为何值时,年利润的预报值最大?
2.(2021 年汕头模拟)二手车经销商小王对其所经营的A 型号二手汽车的使用年数 x 与销售价格 y(单位:万元/辆)进行整理,得到如下数据:
下面是 z 关于 x 的折线图:
(1)由折线图可以看出,可以用线性回归模型拟合 z 与
x 的关系,请用相关系数加以说明;
(2)求 y 关于 x 的回归方程,并预测某辆 A 型号二手车当使用年数为 9 年时售价约为多少?(b,a 小数点后保留两位有效数字)
(3)基于成本的考虑,该型号二手车的售价不得低于 7118 元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
适用于新高考新教材备战2025届高考数学一轮总复习第10章统计与成对数据的统计分析第3节成对数据的统计分析课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第10章统计与成对数据的统计分析第3节成对数据的统计分析课件新人教A版,共52页。PPT课件主要包含了强基础固本增分,研考点精准突破,目录索引,样本相关系数,正相关,负相关,2经验回归方程,2独立性检验,参考数据等内容,欢迎下载使用。
高考数学一轮总复习课件第8章统计与统计分析第1讲随机抽样(含解析): 这是一份高考数学一轮总复习课件第8章统计与统计分析第1讲随机抽样(含解析),共39页。PPT课件主要包含了分层随机抽样,比例是相同的,题组一,走出误区,先后顺序有关,及分层有关,答案1×,2×3√,题组二,走进教材等内容,欢迎下载使用。
2024届高考数学一轮总复习第八章统计与统计分析第三讲成对数据的统计分析课件: 这是一份2024届高考数学一轮总复习第八章统计与统计分析第三讲成对数据的统计分析课件,共59页。PPT课件主要包含了回归分析,独立性检验,12×2列联表,2独立性检验,名师点睛,A①②,B①④,C③④,D②③,答案C等内容,欢迎下载使用。












