新高考数学一轮复习基础巩固9.1 切线方程（精讲）（含解析）

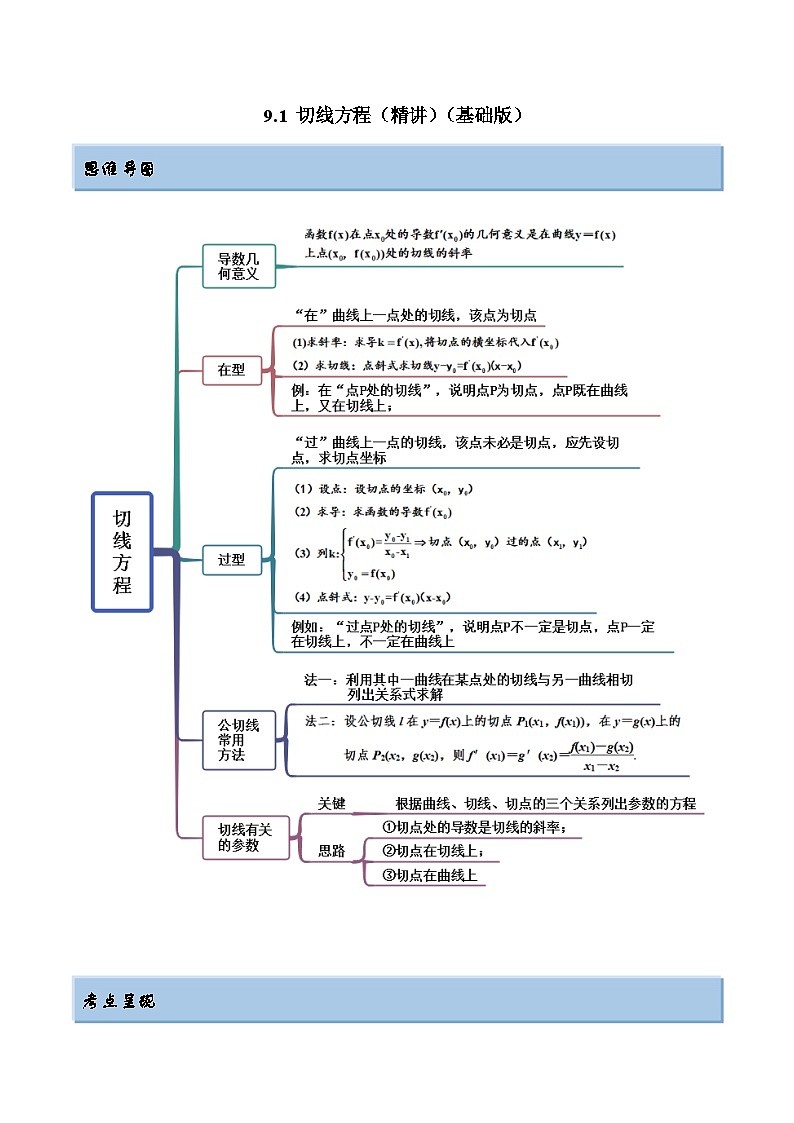
这是一份新高考数学一轮复习基础巩固9.1 切线方程（精讲）（含解析），共11页。试卷主要包含了导数几何意义，在型求切线，过型求切线，根据切线求参数等内容，欢迎下载使用。
9.1 切线方程（精讲）（基础版）  考点一 导数几何意义【例1-1】（2022·日照模拟）曲线 在 处的切线的倾斜角为 ，则 的值为（　　）  A． B． C． D．【答案】B【解析】根据已知条件， ，因为曲线 在 处的切线的倾斜角为 ， 所以 ，所以 .因为 ， ，则解得 ， ，故 .故答案为：B.【例1-2】（2022·枣庄模拟）曲线在点处的切线与直线垂直，则的值为（　　）A．-1 B．0 C．1 D．2【答案】C【解析】设，则，直线的斜率为，由题意可得，解得.故答案为：C.【例1-3】（2022高三下·安徽期中）已知，则曲线在点处的切线的斜率为（　　）A． B． C． D．【答案】D【解析】对，求导可得，，得到，所以，，所以，，故答案为：D【一隅三反】1．（2023高三上·江汉开学考）若函数在点（1，f（1））处的切线的斜率为1，则的最小值为（　　）A． B． C． D．【答案】A【解析】由已知，所以，，当且仅当时等号成立．故答案为：A．2．（2022·宜春模拟）已知函数是定义在R上的奇函数，且，则函数的图象在点处的切线的斜率为（　　）A．-21 B．-27 C．-24 D．-25【答案】A【解析】是奇函数，恒成立，所以，，，所以，，即，．故答案为：A．3．（2022·成都模拟）若曲线在点（1，2）处的切线与直线平行，则实数a的值为（　　）A．－4 B．－3 C．4 D．3【答案】B【解析】 ， 所以 。故答案为：B考点二 在型求切线【例2-1】（2022·贵州模拟）曲线在点处的切线方程为（　　）A． B． C． D．【答案】B【解析】因为 ，所以曲线 在点 处的切线的斜率为 ，当x=1时，y=0，切点坐标为（1，0）.故所求切线方程为 . 故答案为：B【例2-2】（2022海南）曲线：在点处的切线方程为___________【答案】【解析】因为，，，又，所求的切线方程为，即，故答案为：.
【例2-3】（2022福州模拟）已知函数 为偶函数，当x＜0时， ，则曲线 在x＝1处的切线方程为（　　）   A．x-y＝0 B．x-y-2＝0 C．x+y-2＝0 D．3x-y-2＝0【答案】A【解析】当 时， ， ，又函数 为偶函数，所以 ， ，所以 ， ，故切线方程为 ，即 .故答案为：A．【一隅三反】1．（2022高三上·杭州期末）函数在点处的切线方程是　     　.【答案】y=1【解析】因为，所以切线斜率，所以切线方程为y=1. 故答案为：y=12．（2022·广东模拟）已知为奇函数，当时，，则曲线在点处的切线方程为　     　.【答案】y=2x-e【解析】由题意时 ，是奇函数，  时    ， ， ，由点斜式直线方程得   ，整理得y=2x-e ；故答案为：y=2x-e .3．（2021·海南模拟）已知偶函数 满足 ，且在 处的导数 ，则曲线 在 处的切线方程为（　　）  A． B． C． D．【答案】A【解析】由条件知 ，所以 ， 从而 ，即函数 的周期为4.在 中，令 得 ，所以 ，又 ，所以曲线 在 处的切线方程为 ，即 .故答案为：A.考点三 过型求切线【例3-1】.(2022·豫北)已知f(x)＝x2，则过点P(－1，0)，曲线y＝f(x)的切线方程为          【答案】y＝0或4x＋y＋4＝0【解析】易知点P(－1，0)不在f(x)＝x2上，设切点坐标为(x0，x)，由f(x)＝x2可得f′(x)＝2x，∴切线的斜率k＝f′(x0)＝2x0.∵切线过点P(－1，0)，∴k＝＝2x0，解得x0＝0或x0＝－2，∴k＝0或－4，故所求切线方程为y＝0或4x＋y＋4＝0.【例3-2】(2022·江西)过点P(1,1)且与曲线y＝x3相切的直线的条数为            【答案】2【解析】　当点P为切点时，∵y′＝3x2，∴y′|x＝1＝3，则曲线y＝x3在点P处的切线方程为y－1＝3(x－1)，即3x－y－2＝0.当点P不是切点时，设直线与曲线切于点(x0，y0)(x0≠1)，则k＝＝＝x＋x0＋1.∵y′＝3x2，∴y′|x＝x0＝3x，∴2x－x0－1＝0，∴x0＝1(舍)或x0＝－，∴过点P(1,1)与曲线y＝x3相切的直线方程为3x－4y＋1＝0.综上，过点P的切线有2条【一隅三反】1．（2021·永州模拟）曲线 在 处的切线 过原点，则 的方程是（　　）   A． B． C． D．【答案】A【解析】曲线 切点为 ， 所以切线 的斜率 ，又直线 过原点，所以 ，得 ， ．所以 ，故切线 的方程为 即 ．故答案为：A．2．（2021·浙江高三专题练习）过曲线上一点的切线的斜率为，则点的坐标为______．【答案】或.【解析】由可得，设切点，由题意可得，解得：，即，当时，，此时点的坐标为当时，，此时点的坐标为，故答案为：或.3．（2022·广东佛山市）已知函数的图象是经过原点的曲线（非直线），且在原点处的切线方程为，请写出一个符合条件函数的解析式____________．【答案】（或，，等）.【解析】由题意可知：，取，此时，故符合，故答案为：（或，，等）. 考点四 根据切线求参数【例4-1】（2022·岳阳模拟）已知a，为正实数，直线与曲线相切，则的最小值是（　　）A．6 B． C．8 D．【答案】C【解析】设切点为（m，n）， y＝ln（x+b）的导数为，由题意可得=1，又n＝m﹣2a，n＝ln（m+b），解得n＝0，m＝2a，即有2a+b＝1，因为a、b为正实数，所以，当且仅当时取等号，故的最小值为8。故答案为：C．【例4-2】（2022·柳州模拟）已知直线 是曲线 的一条切线，则b＝　     　．【答案】2【解析】函数的定义域为（0，+∞） ， 则，令 ，则x=1 ，
所以切点为（1，3） ，代入y=x+b ，得1+b=3 ，所以b=2 .故答案为：23．（2022·新高考Ⅰ卷）若曲线  有两条过坐标原点的切线，则a的取值范围是　            　.  【答案】a＞0或a＜-4【解析】易得曲线不过原点，设切点为(x0，(x0+a)ex0)，则切线斜率为f(x0)=(x0+a+1)ex0 ，
可得切线方程为y-(x0+a)ex0=(x0+a+1)ex0(x-x0)，又切线过原点，
可得-(x0+a)ex0=-x0(x0+a+1)ex0，化简得 (※)，
又切线有两条， 即方程※有两不等实根，由判别式△=a2+4a>0，得a<-4或a>0.
故答案为：a<-4或a>0.
   【一隅三反】1．（2022·重庆模拟）已知 为非零实数，直线 与曲线 相切，则 　     　.  【答案】e【解析】设切点坐标为 ，对函数 求导得 ， 所以切线方程为 ，所以 ，可得 ， .故答案为：e.2．（2022·晋中模拟）若直线y=2x+a是函数的图象在某点处的切线，则实数　     　.【答案】-1【解析】【解答】设切点坐标为，则所以.故答案为：-1.
3．（2021高三上·德州期中）函数 在 处的切线与直线 平行，则实数 的值为　     　.  【答案】1【解析】因为 ，所以 ， 所以 ，所以函数 在 处的切线的斜率为 ，又因为函数 在 处的切线与直线 平行，所以 ，解得 故答案为：1
4．（2021高三上·安庆月考）已知函数 的图象在点 处的切线的斜率为 ，则 的值为　     　.  【答案】-1【解析】由题意，函数 ，可得 ，所以 ， 因为函数 的图象在点 处的切线的斜率为 ，可得 ，即 ，所以 ，解得 .故答案为：-1.5．（2020高三上·内蒙古期中）若函数 （ 为常数）存在两条均过原点的切线，则实数a的取值范围是　        　.   【答案】【解析】由题意得 的定义域为 ，且 ，设切点坐标为 ，则过原点的切线斜率 ，整理得 存在两条过原点的切线， 存在两个不同的解.设 ，则问题等价于 于 存在两个不同的交点，又 当 时， ， 单调递增，当 时， ， 单调递减， .又当 时， ；当 时， ，若 于 存在两个不同的交点，则 .解得 .故答案为：