

新高考数学一轮复习基础巩固9.4 单调性的分类讨论(精讲)(含解析)
展开
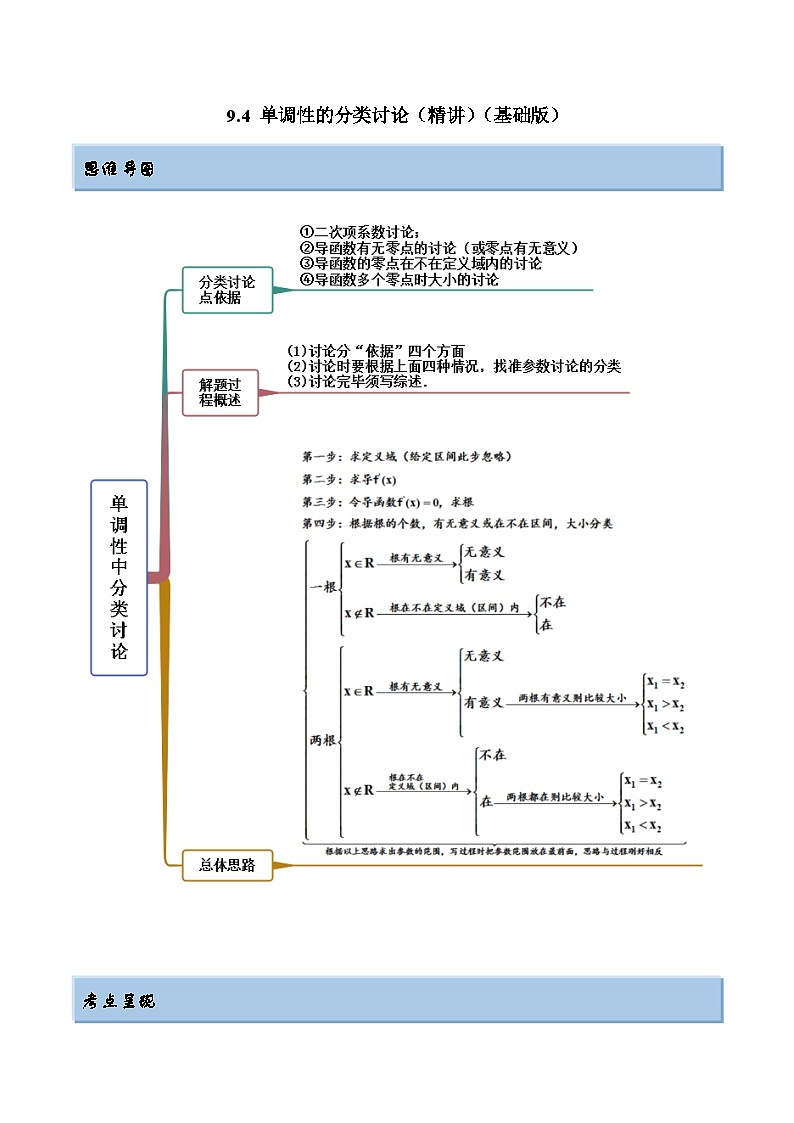
这是一份新高考数学一轮复习基础巩固9.4 单调性的分类讨论(精讲)(含解析),共10页。试卷主要包含了一根型,两根型,判别式型等内容,欢迎下载使用。
9.4 单调性的分类讨论(精讲)(基础版) 考点一 一根型【例1】(2022·河北邯郸·高三开学考试)已知函数,讨论函数的单调性;【答案】答案见解析【解析】由题意得函数的定义域为,当时,令,得,所以在上单调递增;令,得,所以在上单调递减;当时,因为恒成立,所以在上单调递增;【一隅三反】1.(2022·福建·高三阶段练习)已知函数,讨论的单调性;【答案】答案见解析【解析】因为,所以.若,则恒成立;若,则当时,,当时,.故当时,的单调递增区间为,无单调递减区间;当时,的单调递增区间为,单调递减区间为.2.(2022·河南)已知函数,讨论的单调性;【答案】答案见解析【解析】的定义域为,.当时,令,得,令,得,所以在上单调递增,在上单调递减;当时,令,得,令,得,,所以在上单调递增,在上单调递减.综上,当时,在上单调递增,在上单调递减;当时,在上单调递增,在上单调递减.3.(2022·安徽·高三开学考试)已知函数,讨论函数在上的单调性;【答案】答案见解析;【解析】由题意得,,当时,,则函数在上单调递增;当时,令,解得;当时,,则函数在上单调递增;当时,,函数在上单调递减,综上,当时,函数在上单调递增;当时,函数在上单调递增,在上单调递减.考点二 两根型【例2-1】(2022·辽宁·沈阳市第四中学高三阶段练习)已知函数,讨论函数的单调性;【答案】答案见解析【解析】的定义域为,.当时,在区间递减;在区间递增.当时,在上递增.当时,在区间递减;在区间递增.【例2-2】(2022·黑龙江·哈尔滨三中高三阶段练习)已知函数.(1)当时,求曲线在点的切线方程;(2)讨论函数的单调性.【答案】(1)(2)答案见解析【解析】(1)由,则,,,,切线方程:,则.(2)由,求导得,①当时,,,解得,,解得,则:单减区间:,单增区间:;②当时,令,解得或(舍去)当时,,当时,,则:单减区间:,单增区间:;③当时,令,解得或,当时,,当时,,则:单减区间:和,单增区间:;④当时,,则:单减区间:;⑤当时,令,解得或,当时,,当时,,则:单减区间:和,单增区间:;综上,当时,单减区间:,单增区间:当时,单减区间:和,单增区间:当时,单减区间:当时,单减区间:和,单增区间:.【一隅三反】1.(2022·辽宁锦州)已知函数,其中为实常数.(1)当时,求曲线在点处的切线方程;(2)讨论的单调性;【答案】(1)(2)答案详见解析【解析】(1),所以,所以切线方程为.(2)的定义域为,,当时,在区间递减;在区间递增.当时,,在上递减.当时,在区间递减;在区间递增.2.(2022·全国·高二课时练习)求函数的单调区间.【答案】见解析【解析】因为,所以.由,解得x=0或x=2a.当a=0时,,所以f(x)在R上严格增,单调增区间为;当时,当时,;当时,,所以f(x)的单调增区间为及,单调减区间为(0,2a);当时,当时,;当时,,所以f(x)的单调增区间为及,单调减区间为(2a,0).3.(2022·湖北·襄阳五中高三开学考试)已知函数(其中为自然对数的底数).讨论的单调性;【答案】见解析【解析】由可得,当时,,当时,,当时,,从而的单调递增区间为,单调递减区间为;当时,由得,,,①若,即时,恒成立,故在R上单调递增:②若,即时,由可得,或.令可得,此时的单调递增区间为和,单调递减区间为;③若,即时,由可得,或,令可得,此时的单调递增区间为和,单调递减区间为;综上所述,当时,的单调递增区间为,单调递减区间为;当时,在R上单调递增;当时,的单调递增区间为和,单调递减区间为;当时,的单调递增区间为和,单调递减区间为;考点三 判别式型【例3】(2022·福建泉州·模拟预测)已知函数讨论的单调性;【答案】(1)当时,在上单调递增;当或时,在上单调递减,在和上单调递增.【解析】由,求导得,易知恒成立,故看的正负,即由判别式进行判断,①当时,即,,则在上单调递增;②当时,即或,令时,解得或,当时,,则在上单调递减;当或,,则在和上单调递增;综上所述,当时,在上单调递增;当或时,在上单调递减,在和上单调递增.【一隅三反】1.(2022·全国·高三专题练习)已知函数,记的导函数为,讨论的单调性;【答案】见解析【解析】由已知可得,故可得.当时,,故在单调递增;当时,由,解得,或,记,,则可知当变化时,的变化情况如下表:00极大值极小值所以,函数在区间单调递增,在区间单调递减,在区间单调递增.2.(2022山西)若函数,,为常数,求函数的单调区间;【答案】见解析【解析】的定义域为,①当,,所以,的单调增区间为,无单调减区间; ②当时,,解得,,所以的单调增区间为,,单调递减区间为3(2022黑龙江)已知函数,令,讨论函数的单调性;【答案】详见解析【解析】,,当时,恒成立,函数的单调递减区间是,无单调递增区间;当时, ,(ⅰ)时,即时,的解集是,的解集是 ,所以函数的单调递增区间是,函数的单调递减区间是;(ⅱ)当时,即时,函数恒成立,即函数的单调递减区间是,无单调递增区间;综上可知,当时,函数的单调递减区间是,无单调递增区间;当时,函数的单调递增区间是,函数的单调递减区间是.
相关试卷
这是一份新高考数学一轮复习基础巩固10.4 双曲线(精讲)(含解析),共18页。试卷主要包含了双曲线的定义及应用,双曲线的离心率及渐近线,双曲线的标准方程,直线与双曲线的位置关系,弦长与中点弦等内容,欢迎下载使用。
这是一份新高考数学一轮复习基础巩固10.3 椭圆(精讲)(含解析),共14页。试卷主要包含了椭圆的定义及应用,椭圆的离心率,椭圆的标准方程,直线与椭圆的位置关系,弦长等内容,欢迎下载使用。
这是一份新高考数学一轮复习基础巩固10.2 圆的方程(精讲)(含解析),共12页。试卷主要包含了圆的方程,直线与圆的位置关系,圆与圆的位置关系,切线问题等内容,欢迎下载使用。









