新高考数学一轮复习基础巩固9.2 利用导数求单调性（精讲）（含解析）

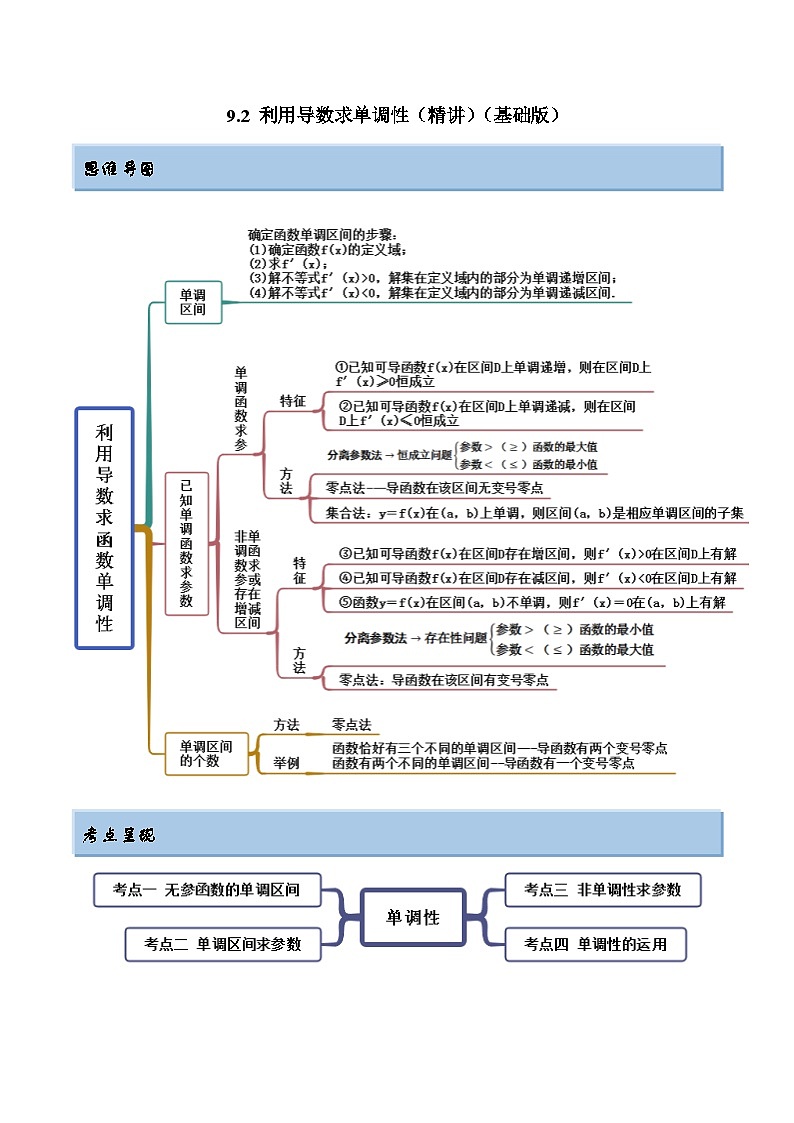
这是一份新高考数学一轮复习基础巩固9.2 利用导数求单调性（精讲）（含解析），共12页。试卷主要包含了无参函数的单调区间，单调函数求参数，非单调函数求参数，单调性的运用等内容，欢迎下载使用。
9.2 利用导数求单调性（精讲）（基础版）考点一 无参函数的单调区间【例1】（2022高二下·滦南期末）函数单调递减区间是（　　）A． B． C． D．【答案】D【解析】f′(x)=， 令f′(x)<0，解得：1<x<e，故f(x)在(1，e)递减，故答案为：D.【一隅三反】1．（2022·全国课时练习）函数的单调递增区间是（    ）A． B． C． D．【答案】D【解析】，由，得，所以函数的单调递增区间是．故选：D.2（2022·全国·课时练习）函数的单调递增区间为（    ）A． B． C． D．【答案】B【解析】函数的定义域为，，令，得，解得，故函数的单调递增区间为．故选：B．  3．（2022·全国·高三专题练习（文））函数的单调递减区间为__________．【答案】【解析】当时，，则其在上递减，当时，，则，当时，，所以在上递减，综上，的单调递减区间为，故答案为：考点二 单调函数求参数【例2-1】（2022高三上·成都开学考）若函数在区间上单调递增，则实数的取值范围是（　　）A． B． C． D．【答案】B【解析】由题意，已知条件等价为在上恒成立，即在上恒成立，，在上单调递减，，，的取值范围是.故答案为：B.【例2-2】（2022·浙江）已知函数在区间上是减函数，则实数的取值范围为（    ）A． B． C． D．【答案】B【解析】由题意，在上恒成立，即在上恒成立，因为在上单调递增，所以，所以在时，，所以.故选：B【一隅三反】1．（2022·新疆）若函数在区间上单调递增，则实数a的取值范围是（    ）A． B． C． D．【答案】B【解析】依题意在区间上恒成立，即在区间上恒成立.令，则，所以在上单调递增，则，所以.故选:B.2．（2022·河南）若函数在上单调递增，则实数a的取值范围是（    ）A． B． C． D．【答案】B【解析】，又在上单调递增，故在上恒成立，而时，易见，只需要即可，故.故选：B.3．（2022·惠州模拟）若函数在上单调递增，则实数的取值范围是　         　．【答案】【解析】因为，所以，又函数在上单调递增，所以在恒成立，分离参数可得在恒成立，令，，所以在上单调递增，所以，所以，故答案为：. 考点三 非单调函数求参数【例3-1】（2022·黑龙江）若函数在区间内存在单调递增区间，则实数a的取值范围是（    ）A． B． C． D．【答案】D【解析】由可得：.因为函数在区间内存在单调递增区间，所以在上有解，即在上有解.设，由在上恒成立，所以在单调递增，所以.所以.故选：D【例3-2】（2022·北京十四中高三开学考试）若函数在区间上不是单调函数，则实数k的取值范围是（    ）A．或或 B．或C． D．不存在这样的实数【答案】B【解析】，令，解得，或，所以当或时，当时，所以在和上单调递增，在上单调递减，即函数极值点为，若函数在区间上不是单调函数，则或，所以或，解得或故选：B．【例3-3】（2022·上海）已知函数存在三个单调区间，则实数的取值范围是（    ）A． B．C． D．【答案】C【解析】由题意，函数，可得，因为函数存在三个单调区间，可得有两个不相等的实数根，则满足，解得或，即实数的取值范围是.故选：C.【一隅三反】1．（2022·福建·莆田一中）已知函数在区间上不是单调函数，则实数的取值范围是（    ）A． B． C． D．【答案】A【解析】因为在区间上不是单调函数，所以在区间上有解，即在区间上有解．令，则．当时，；当时，．故在上单调递减，在上单调递增．又因为，且当时，所以在区间上单调递增，所以，解得.故选：A2．（2022北京）若函数存在递减区间，则实数的取值范围是（    ）A． B．C． D．【答案】B【解析】由题设，，由存在递减区间，即存在使，∴，可得或.故选：B3．（2022·全国·高三专题练习（文））若函数在定义域内的一个子区间上不是单调函数，则实数k的取值范围是（    ）A． B． C．(1，2] D．[1，2)【答案】A【解析】显然函数的定义域为，．由，得函数的单调递增区间为；由，得函数单调递减区间为．因为函数在区间上不是单调函数，所以，解得，又因为为定义域内的一个子区间，所以，即．综上可知实数k的取值范围是．故选：A4．（2022·云南）若函数恰好有三个不同的单调区间，则实数的取值范围是（    ）A． B． C． D．【答案】D【解析】由题意得，函数恰好有三个不同的单调区间，有两个不同的零点，所以，，解得.因此，实数的取值范围是.故选：D.考点四 单调性的运用【例4-1】（2022·湖北模拟）已知函数，不等式的解集为（　　）A． B．C． D．【答案】B【解析】因为，所以，所以在上单调递减，则等价于，解得，即原不等式的解集为.故答案为：B.【例4-2】（2022·湖北模拟）已知：，，，则、、大小关系为（　　）A． B． C． D．【答案】B【解析】令，则，当时，，所以函数在上递增，所以，即，又，所以，所以，又，所以，，所以，所以.故答案为：B.【例4-3】．（2022·四川·遂宁中学外国语实验学校高三开学考试（理））设是函数的导函数，的图像如图所示，则的图像最有可能的是（    ）A． B．C． D．【答案】C【解析】由导函数的图象可得当时，,函数单调递增；当时，,函数单调递减；当时，,函数单调递增.只有C选项的图象符合.故选:C.【一隅三反】1．（2022·江阴模拟）已知，则，，的大小为（　　）A． B． C． D．【答案】C【解析】令函数，当时，求导得：， 则函数在上单调递减，又，，，显然，则有，所以.故答案为：C2．（2022·全国课时练习）已知函数在定义域内可导，其图象如图所示.记的导函数为，则不等式的解集为（    ）A． B．C． D．【答案】A【解析】对于不等式对，当时，，则结合图象，知原不等式的解集为；当时，，则结合图象，知原不等式的解集为．综上，原不等式的解集为．故选：A3．（2022·湖北模拟）已知定义域为R的函数，有且，，则的解集为　                        　．【答案】【解析】，在为增函数，又为偶函数，∴，则，得或，解集为故答案为：．