新高考数学一轮复习基础巩固9.3 利用导数求极值最值（精讲）（含解析）

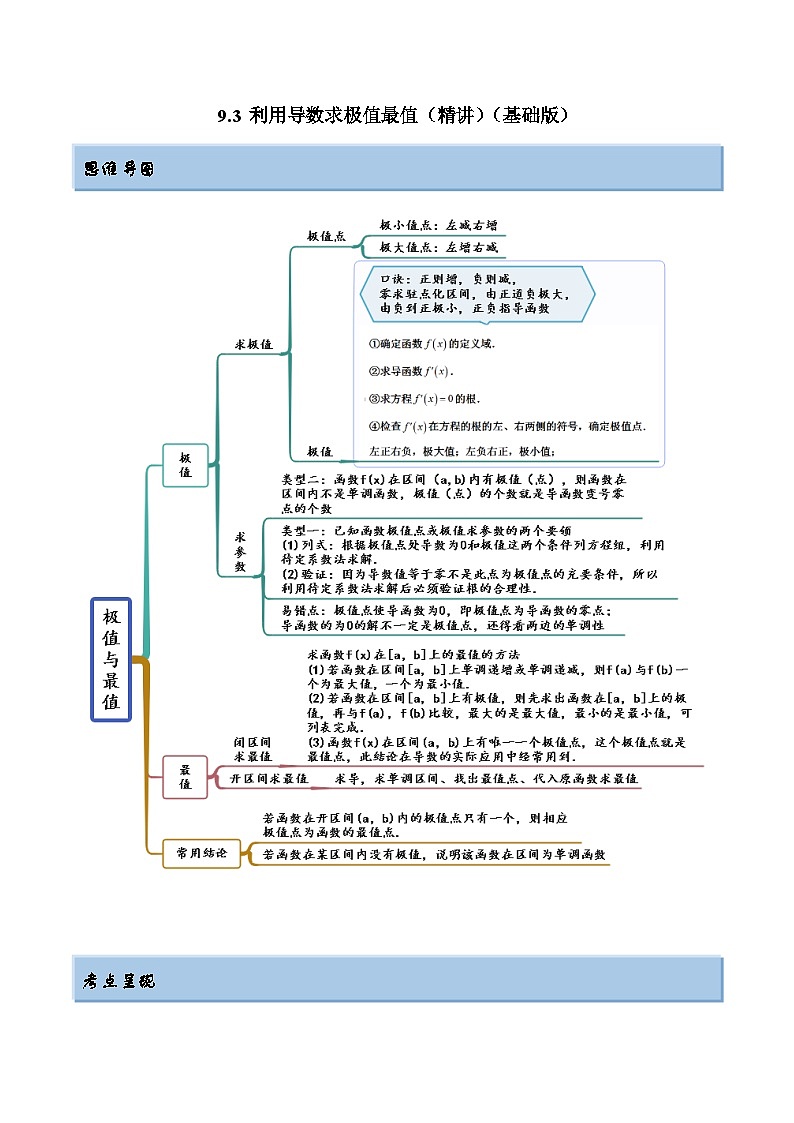
这是一份新高考数学一轮复习基础巩固9.3 利用导数求极值最值（精讲）（含解析），共13页。试卷主要包含了极值，最值，已知极值最值求参数等内容，欢迎下载使用。
9.3 利用导数求极值最值（精讲）（基础版）  考点一 极值【例1-1】（2022·崇左模拟）函数的极小值是　     　．【答案】2【解析】由题意可得．由，得或；由，得，则在和上单调递增，在上单调递减，则． 故答案为：2【例1-2】（2022·辽阳二模）设函数 ，则下列不是函数 极大值点的是（　　）  A． B． C． D．【答案】D【解析】由题可得 ， 令 ，得 或 ， ，则当 时， ，当 时， ，所以函数 在 ， ， 上单调递增，在 ， ， 上单调递减，故不是函数 极大值点的是 .故答案为：D.【例1-3】（2022·安康模拟）若函数有两个极值点，则实数的取值范围为（　　）A． B．C． D．【答案】D【解析】由，得.因为函数有两个极值点，所以有两个不同的解，即有两个不同的解转化为   与   的图象有两个交点；设，则，令 ，即 ，解得   当时，；当时，；所以在上单调递增，在上单调递减.分别作出函数与   的图象，如图所示由图可知，0   ，解得   .所以实数   的取值范围为   .故答案为：D.【一隅三反】1（2022高三上·襄阳期末）已知函数，，则所有极值点的和为（　　）A． B．13π C．17π D．【答案】D【解析】，令，得，因为在两侧异号，所以是函数的极值点，又，所以极值点，所以所有极值点的和为，故答案为：D.2．（2022·昆明模拟）若是函数的极值点，则的极大值为（　　）A．-1 B． C． D．1【答案】C【解析】因为，故可得，因为是函数的极值点，故可得，即，解得，此时令，解得，由可得或；由可得，所以在区间单调递增，在单调递减，在单调递增，故的极大值点为，则的极大值为。故答案为：C.3（2022·河西模拟）若函数在处取得极值，则　     　．【答案】1【解析】，因为函数在处取得极值，所以，，解得，此时，，故当时，，单调递减；当和时，，单调递增；所以，函数在处取得极小值，满足题意，所以，所以故答案为：1考点二 最值【例2】（2021·浙江）已知函数，则的最大值是_____，最小值是______．【答案】；    .    【解析】，，又，令，得；令，得.在上单调递减，在上单调递增，，的最大值是2；最小值是.故答案为：；.【一隅三反】1．（2021·全国专题练习）函数的最大值为（    ）A． B． C． D．【答案】D【解析】函数的定义域为，则令，解得，当时，，则函数单调递增；当时，，则函数单调递减，则当时，函数有最大值，为，故选:D.2（2021·江苏）已知函数，则的最小值是（    ）A． B． C． D．【答案】C【解析】由题得，所以当时，单调递增；当时，单调递减.所以取得最小值时，，此时，当时，；当时，；所以的最小值是.故选：C3．（2021·甘肃兰州市）函数的最大值为（    ）A． B． C． D．【答案】B【解析】由，得，当时，，当时，，所以函数在上递减，在上递增，因为，所以函数的最大值为，故选：B考点三 已知极值最值求参数【例3-1】（2022·新疆三模）若函数在处有极值10，则（　　）A．6 B．-15 C．-6或15 D．6或-15【答案】B【解析】，又 时 有极值10，解得 或当 时，此时 在 处无极值，不符合题意经检验， 时满足题意故答案为：B【例3-2】（2022·凉山模拟）函数，若在上有最小值，则实数a的取值范围是（　　）A． B． C． D．【答案】A【解析】由题意，函数，可得，若时，当时，可得，在上单调递减，此时函数在没有最小值，不符合题意；当时，令，即，即与的交点，画出函数与的图象，如图所示，结合图象，可得存在，使得，当时，，单调递减；当时，，单调递增，此时函数在上有最小值，符合题意，综上可得，实数a的取值范围是.故答案为：A.【例3-3】（2022高三上·开封开学考）已知函数的值域为，则实数的取值范围是（　　）A． B． C． D．【答案】D【解析】当时，在上单调递增，，，则在上值的集合是， 当时，，，当时，，当时，，即在上单调递减，在上单调递增，，，则在上值的集合为，因函数的值域为，于是得，则，解得，所以实数的取值范围是.故答案为：D【一隅三反】1（2021高三上·江西月考）设函数若无最大值，则实数的取值范围是（　　）A． B． C． D．【答案】A【解析】因为作出函数与直线的图象，它们的交点是，，，由，则令，可得或，当或时，，则单调递增，当时，，则单调递减，所以是的极大值点，是的极小值点，由图象可知，当时，有最大值或，当时，有，此时无最大值，故实数的取值范围为.故答案为：A.2．（2022金台月考）已知函数有两个极值点，则实数的取值范围是（　　）A． B． C． D．【答案】B【解析】由题意有两个不等实根，即有两个不等实根，设，则，当时，，递增，当时，，递减，时，为极大值也是最大值，时，，且，当时，，所以当，即时，直线与的图象有两个交点，即有两个不等实根．故答案为：B3（2022潍坊期中）若函数 在 上无极值，则实数 的取值范围（　　）  A． B． C． D．【答案】D【解析】由 可得 ， 恒成立， 为开口向上的抛物线，若函数 在 上无极值，则 恒成立，所以 ，解得： ，所以实数 的取值范围为 ，故答案为：D.4．（2021·全国高三专题练习）若函数在区间上存在最小值，则的取值范围是A． B． C． D．【答案】C【解析】，，令，解得或；令，解得.故的单调递增区间为和，单调递减区间为，所以，函数在处取得极小值，由于函数在区间内取到最小值，则，由可得，可得,即，解得.因此，实数的取值范围是.故选：C.