新高考数学一轮复习基础巩固10.2 圆的方程（精讲）（含解析）

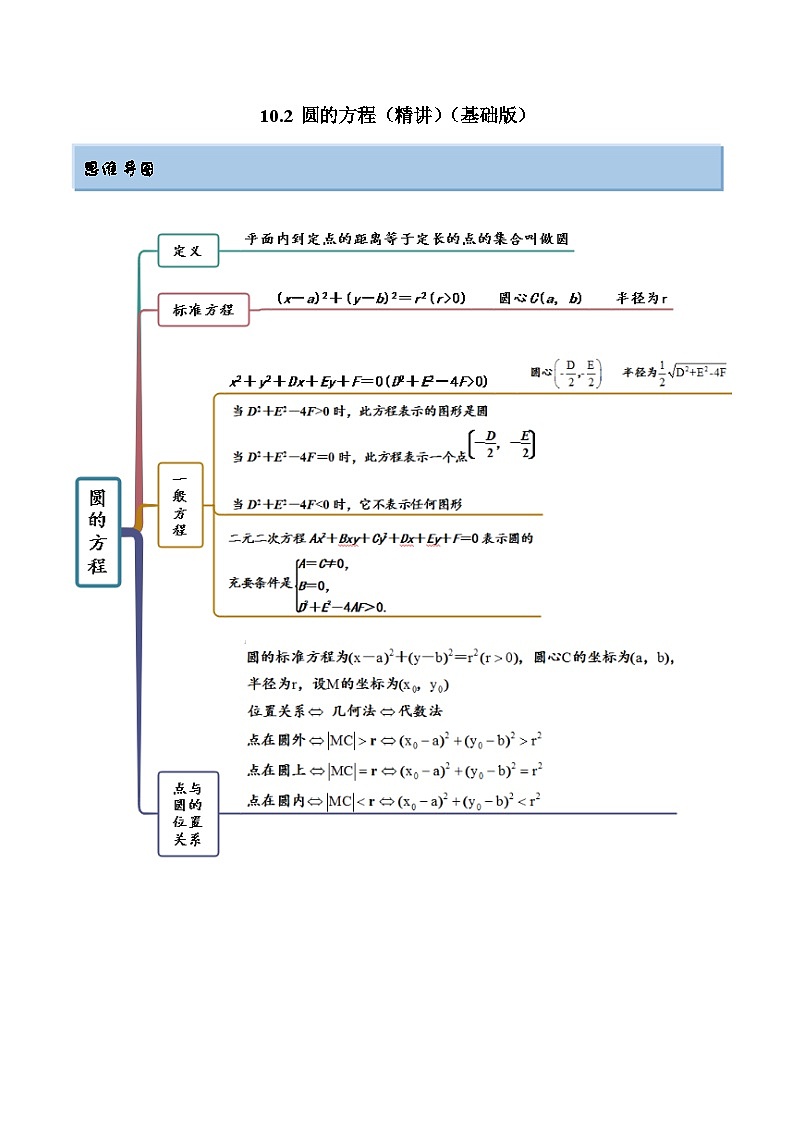
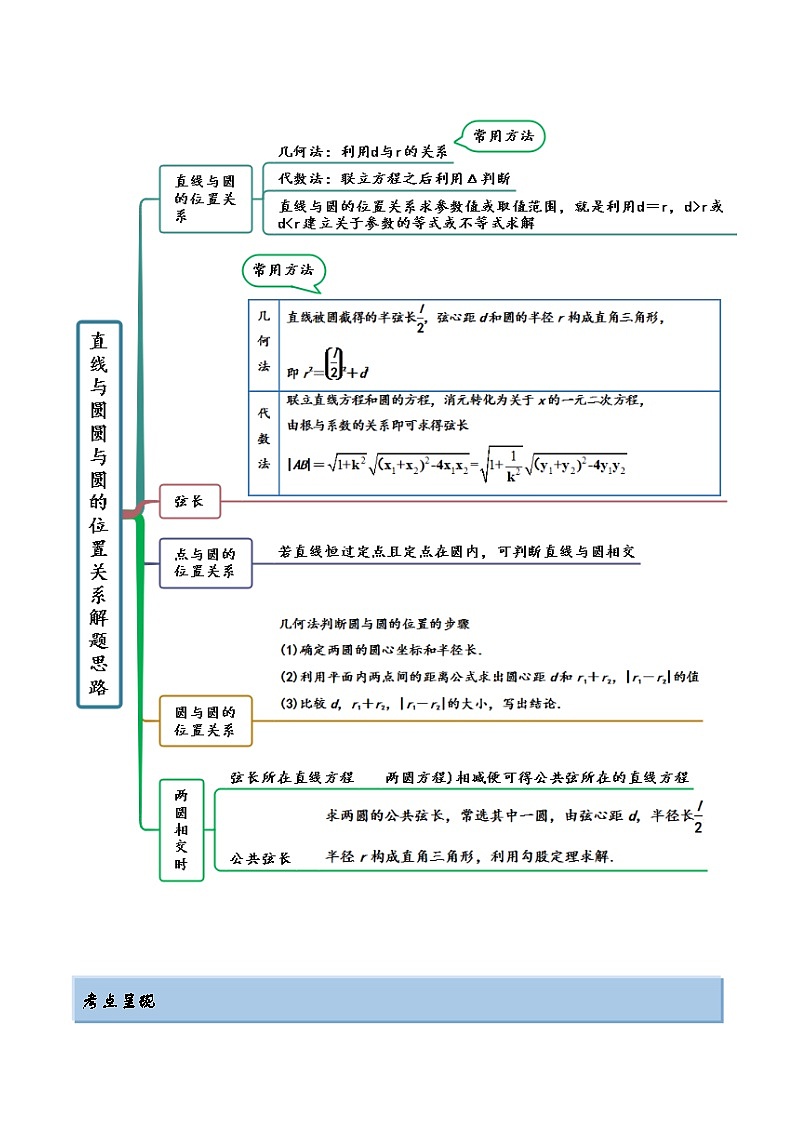
这是一份新高考数学一轮复习基础巩固10.2 圆的方程（精讲）（含解析），共12页。试卷主要包含了圆的方程，直线与圆的位置关系，圆与圆的位置关系，切线问题等内容，欢迎下载使用。
10.2 圆的方程（精讲）（基础版）  考点一 圆的方程【例1-1】（2021白云期末）已知圆的方程为，则圆心的坐标为（　　）A． B． C． D．【答案】A【解析】圆的标准方程为，圆心的坐标为. 故答案为：A.【例1-2】（2022成都）已知圆的圆心在直线上，且圆与轴的交点分别为，则圆的标准方程为（　　）A． B．C． D．【答案】B【解析】由题意设圆心坐标为，再由圆与轴的交点分别为，可得，解得，则圆心坐标为，半径．该圆的标准方程是．故答案为：B．【一隅三反】1．（2022·江西模拟）设甲：实数；乙：方程是圆，则甲是乙的（　　）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【答案】A【解析】若方程表示圆，则，解得：；，，甲是乙的充分不必要条件.故答案为：A.2．（2022和平）圆心在轴上，半径为2，且过点的圆的方程为（　　）A． B．C． D．【答案】B【解析】根据题意，设圆的标准方程为 ， 将代入，求得 ，则圆的标准方程为，故答案为：B.3．（2022杭州）过点（7，-2）且与直线相切的半径最小的圆方程是（　　）A． B．C． D．【答案】B【解析】过点作直线的垂线，垂足为，则以为直径的圆为直线相切的半径最小的圆，其中，设，则，解得：，故的中点，即圆心为，即，故该圆为故答案为：B考点二 直线与圆的位置关系【例2-1】（2022高二下·玉溪期末）已知直线经过点，且与圆相切，则的方程为（　　）A． B． C． D．【答案】A【解析】直线经过点，且与圆相切，则，故直线的方程为，即。故答案为：A.【例2-2】（2022·温州）已知直线与圆有两个不同的交点，则实数的取值范围是（　　）A． B． C． D．【答案】B【解析】因为直线与圆有两个不同的交点，所以圆心到直线的距离，即，解得，所以实数的取值范围是，故答案为：B.【例2-3】（2022·柳州模拟）已知直线 与圆 相交于A，B两点 ，则k＝（　　）  A． B． C． D．【答案】B【解析】圆的圆心C（2，1） ， 半径r=2， 所以圆心C（2，1）到直线 的距离， 而 ，所以 ，解得： .故选：B 【一隅三反】1．（2022·秦皇岛二模）直线被圆截得的弦长为（　　）A． B． C． D．【答案】B【解析】将圆的方程化为：，则圆的圆心为，半径为4，因为圆心到直线的距离为：，所以直线被圆截得的弦长为. 答案为：B.2．（2022·呼和浩特模拟）直线l： 与函数 的图象有两个公共点，则k的取值范围为（　　）  A． B． C． D．【答案】C【解析】直线l： 过点 ， 函数 变形为 其图象如图所示：由图象知： ， ，因为直线l： 与函数 的图象有两个公共点，所以 ，故答案为：C3．（2022·贵阳模拟）已知直线和与圆都相切，则圆的面积的最大值是（　　）A．2π B．4π C．8π D．16π【答案】A【解析】由题，互相平行，且，故圆的直径为间的距离，令，则，，故当，即时取得最大值，此时圆的面积为故答案为：A4．（2022·鞍山模拟）（多选）已知M为圆C：上的动点，P为直线l：上的动点，则下列结论正确的是（　　）A．直线l与圆C相切 B．直线l与圆C相离C．|PM|的最大值为 D．|PM|的最小值为【答案】B,D【解析】圆C：得圆心，半径∵圆心到直线l：得距离∴直线l与圆C相离A不正确，B符合题意；C不正确，D符合题意；故答案为：BD． 考点三 圆与圆的位置关系【例3-1】（2022高一下·汉中期中）已知，，那么它们的位置关系是（　　）A．外离 B．相切 C．相交 D．内含【答案】C【解析】方程可化为，得，， 方程可化为，得，，，，故两圆相交。故答案为：C.【例3-2】（2022·吉林模拟）已知两圆方程分别为和．则两圆的公切线有（　　）A．1条 B．2条 C．3条 D．4条【答案】C【解析】两圆的圆心分别为和，半径分别为2和3，圆心距，则两圆外切，公切线有3条． 故答案为：C【一隅三反】1．（2022·石家庄模拟）（多选）已知圆与圆，则下列说法正确的是（　　）A．若圆与x轴相切，则B．若，则圆与圆相离C．若圆与圆有公共弦，则公共弦所在的直线方程为D．直线与圆始终有两个交点【答案】B,D【解析】因为圆， 所以若圆与x轴相切，则有，A不符合题意；当时，，两圆相离，B符合题意；由两圆有公共弦，两圆的方程相减可得公共弦所在直线方程，C不符合题意；直线过定点，而，故点在圆内部，所以直线与圆始终有两个交点，D符合题意.故答案为：BD2．（2022·徐汇期末）已知圆和圆内切，则m的值为　     　．【答案】【解析】圆的圆心为，半径为，圆的圆心为，半径为，所以两圆的圆心距，又因为两圆内切，有，解得.故答案为：.3（2022广安期末）若圆平分圆的周长，则直线被圆所截得的弦长为　     　．【答案】6【解析】两圆相减得公共弦所在的直线方程为由题知两圆的公共弦过圆的圆心，所以即，又，所以到直线的距离所以直线被圆所截得的弦长为故答案为：6考点四 切线问题【例4-1】（2022·天津市模拟）过点作圆的切线，则的方程为（　　）A． B．或C． D．或【答案】C【解析】即 在圆上则过 点的切线方程为 整理得 故答案为：C【例4-2】（2022·湖北模拟）若圆关于直线对称，则从点向圆作切线，切线长最小值为（　　）A．2 B．3 C．4 D．6【答案】C【解析】由圆，可得，∴圆心，又圆关于直线对称，∴，即，由点向圆所作的切线长为：，即切线长最小值为4.故答案为：C.【一隅三反】1．（2022·朝阳模拟）过点作圆的切线，则切线方程为（　　）A． B．C． D．或【答案】C【解析】由圆心为，半径为， 斜率存在时，设切线为，则，可得，所以，即，斜率不存在时，显然不与圆相切；综上，切线方程为.故答案为：C2．（2022·广西模拟）过圆上一点A作圆的切线，切点为B，则的最小值为（　　）A．2 B． C． D．【答案】B【解析】设圆与圆的圆心分别为O，C，则，当最小时，最小，由于点A在圆O上，则的最小值为，所以的最小值为. 故答案为：B.3．（2022高二下·番禺期末）写出与圆和圆都相切的一条切线方程　                            　.【答案】y=1或24x+7y+25=0或4x-3y-5=0【解析】圆的圆心为，半径为1；圆的圆心为，半径为4， 圆心距为，所以两圆外切，如图，有三条切线，易得切线的方程为y=1，因为，且，所以，设，即，则到的距离，解得（舍去）或，所以，可知和关于对称，联立，解得在上，在上任取一点，设其关于的对称点为，则，解得，则，所以直线，即24x+7y+25=0，综上所述，切线方程为y=1或24x+7y+25=0或4x-3y-5=0。故答案为：y=1或24x+7y+25=0或4x-3y-5=0。