2021年浙江省绍兴市中考数学真题试卷 解析版

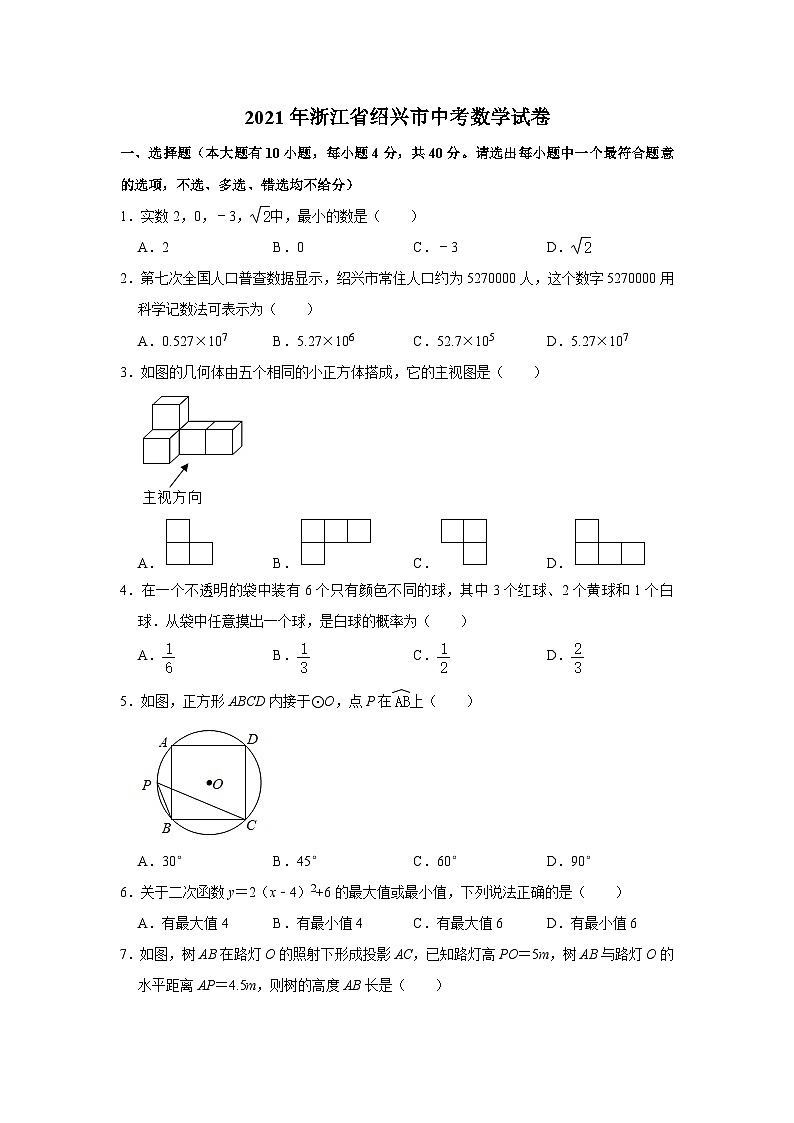
这是一份2021年浙江省绍兴市中考数学真题试卷 解析版，共30页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

2021年浙江省绍兴市中考数学试卷
一、选择题（本大题有10小题，每小题4分，共40分。请选出每小题中一个最符合题意的选项，不选、多选、错选均不给分）
1．实数2，0，﹣3，中，最小的数是（　　）
A．2 B．0 C．﹣3 D．
2．第七次全国人口普查数据显示，绍兴市常住人口约为5270000人，这个数字5270000用科学记数法可表示为（　　）
A．0.527×107 B．5.27×106 C．52.7×105 D．5.27×107
3．如图的几何体由五个相同的小正方体搭成，它的主视图是（　　）

A． B． C． D．
4．在一个不透明的袋中装有6个只有颜色不同的球，其中3个红球、2个黄球和1个白球．从袋中任意摸出一个球，是白球的概率为（　　）
A． B． C． D．
5．如图，正方形ABCD内接于⊙O，点P在上（　　）

A．30° B．45° C．60° D．90°
6．关于二次函数y＝2（x﹣4）2+6的最大值或最小值，下列说法正确的是（　　）
A．有最大值4 B．有最小值4 C．有最大值6 D．有最小值6
7．如图，树AB在路灯O的照射下形成投影AC，已知路灯高PO＝5m，树AB与路灯O的水平距离AP＝4.5m，则树的高度AB长是（　　）

A．2m B．3m C．m D．m
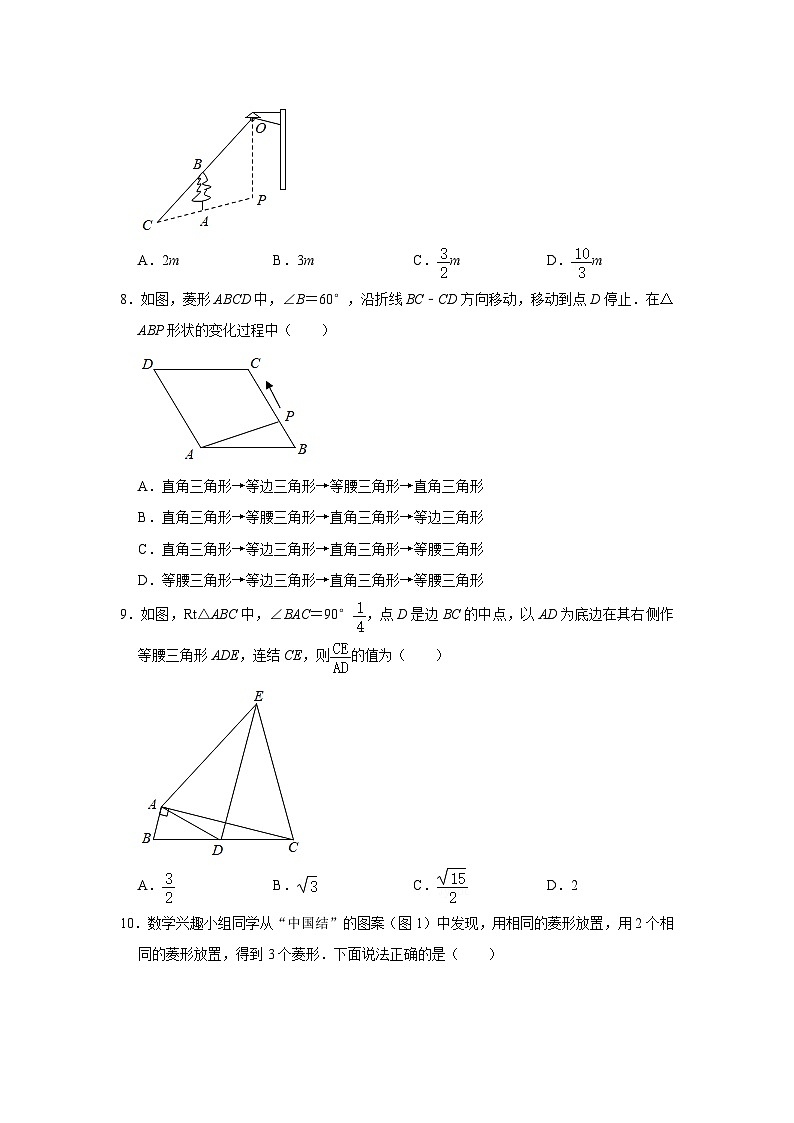
8．如图，菱形ABCD中，∠B＝60°，沿折线BC﹣CD方向移动，移动到点D停止．在△ABP形状的变化过程中（　　）

A．直角三角形→等边三角形→等腰三角形→直角三角形
B．直角三角形→等腰三角形→直角三角形→等边三角形
C．直角三角形→等边三角形→直角三角形→等腰三角形
D．等腰三角形→等边三角形→直角三角形→等腰三角形
9．如图，Rt△ABC中，∠BAC＝90°，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，连结CE，则的值为（　　）

A． B． C． D．2
10．数学兴趣小组同学从“中国结”的图案（图1）中发现，用相同的菱形放置，用2个相同的菱形放置，得到3个菱形．下面说法正确的是（　　）

A．用3个相同的菱形放置，最多能得到6个菱形
B．用4个相同的菱形放置，最多能得到16个菱形
C．用5个相同的菱形放置，最多能得到27个菱形
D．用6个相同的菱形放置，最多能得到41个菱形
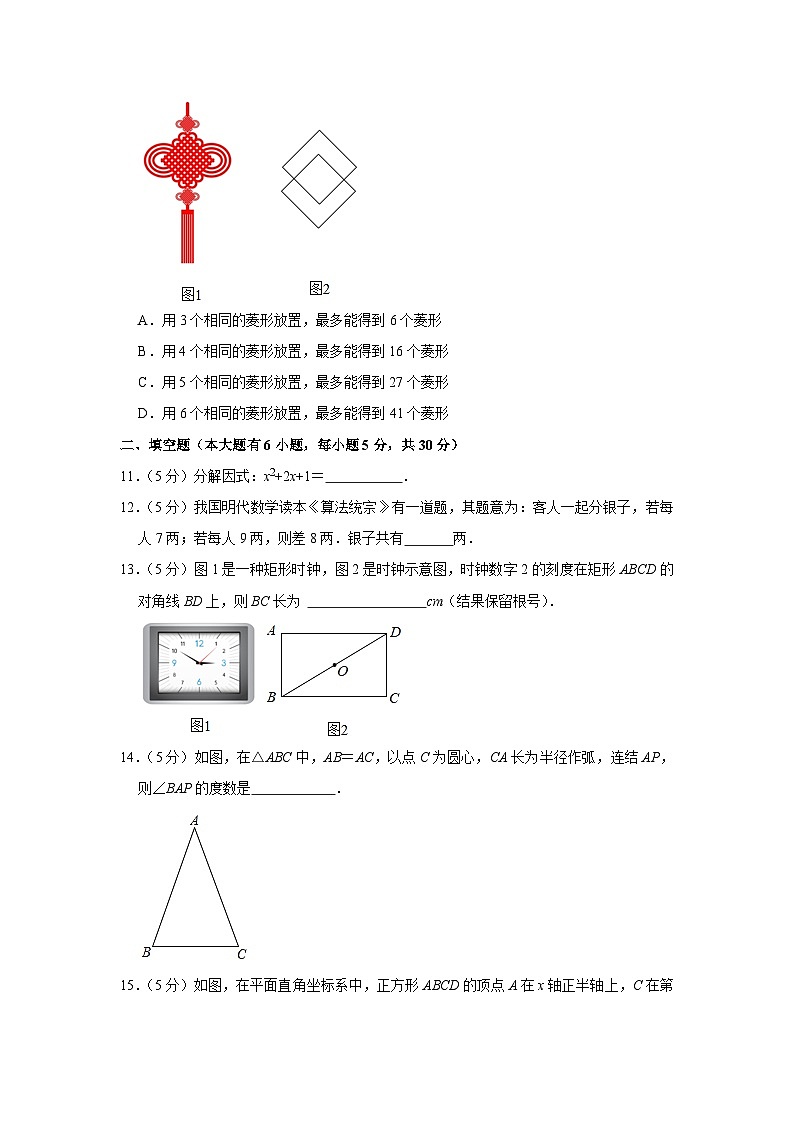
二、填空题（本大题有6小题，每小题5分，共30分）
11．（5分）分解因式：x2+2x+1＝　 　．
12．（5分）我国明代数学读本《算法统宗》有一道题，其题意为：客人一起分银子，若每人7两；若每人9两，则差8两．银子共有　 　两．
13．（5分）图1是一种矩形时钟，图2是时钟示意图，时钟数字2的刻度在矩形ABCD的对角线BD上，则BC长为 　 　cm（结果保留根号）．

14．（5分）如图，在△ABC中，AB＝AC，以点C为圆心，CA长为半径作弧，连结AP，则∠BAP的度数是　 　．

15．（5分）如图，在平面直角坐标系中，正方形ABCD的顶点A在x轴正半轴上，C在第一象限，顶点D的坐标（，2）（常数k＞0，x＞0）的图象恰好经过正方形ABCD的两个顶点，则k的值是　 　．

16．（5分）已知△ABC与△ABD在同一平面内，点C，D不重合，AB＝4，AC＝AD＝2　 　．
三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题8分，第24小题14分，共80分.解答需写出必要的文字说明、演算步骤或证明过程
17．（8分）（1）计算：4sin60°﹣+（2﹣）0．
（2）解不等式：5x+3≥2（x+3）．
18．（8分）绍兴莲花落，又称“莲花乐”，“莲花闹”，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，并将抽查结果绘制成不完整的统计图．

根据图中信息，解答下列问题：
（1）本次接受问卷调查的学生有多少人？并求图2中“了解”的扇形圆心角的度数；
（2）全校共有1200名学生，请你估计全校学生中“非常了解”、“了解”莲花落的学生共有多少人．
19．（8分）Ⅰ号无人机从海拔10m处出发，以10m/min的速度匀速上升，Ⅱ号无人机从海拔30m处同时出发（m/min）的速度匀速上升，经过5min两架无人机位于同一海拔高度b（m）（m）与时间x（min）的关系如图．两架无人机都上升了15min．
（1）求b的值及Ⅱ号无人机海拔高度y（m）与时间x（min）的关系式；
（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

20．（8分）拓展小组研制的智能操作机器人，如图1，水平操作台为l，高AB为50cm，连杆BC长度为70cm，C是转动点，且AB
（1）转动连杆BC，手臂CD，使∠ABC＝143°，如图2，求手臂端点D离操作台l的高度DE的长（精确到1cm，参考数据：sin53°≈0.8，cos53°≈0.6）．
（2）物品在操作台l上，距离底座A端110cm的点M处，转动连杆BC，手臂端点D能否碰到点M？请说明理由．

21．（10分）如图，在△ABC中，∠A＝40°，E分别在边AB，AC上，连结CD，BE．
（1）若∠ABC＝80°，求∠BDC，∠ABE的度数；
（2）写出∠BEC与∠BDC之间的关系，并说明理由．

22．（12分）小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，杯体ACB是抛物线的一部分，抛物线的顶点C在y轴上，且点A，B关于y轴对称，杯高DO＝8，杯底MN在x轴上．
（1）求杯体ACB所在抛物线的函数表达式（不必写出x的取值范围）；
（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯口直径A′B′∥AB，杯脚高CO不变，求A′B′的长．

23．（12分）问题：如图，在▱ABCD中，AB＝8，∠DAB，∠ABC的平分线AE，F，求EF的长．
答案：EF＝2．
探究：（1）把“问题”中的条件“AB＝8”去掉，其余条件不变．
①当点E与点F重合时，求AB的长；
②当点E与点C重合时，求EF的长．
（2）把“问题”中的条件“AB＝8，AD＝5”去掉，其余条件不变，D，E，F相邻两点间的距离相等时，求的值．

24．（14分）如图，矩形ABCD中，AB＝4，点F是对角线BD上一动点，∠ADB＝30°．连结EF
（1）若EF⊥BD，求DF的长；
（2）若PE⊥BD，求DF的长；
（3）直线PE交BD于点Q，若△DEQ是锐角三角形，求DF长的取值范围．


2021年浙江省绍兴市中考数学试卷
参考答案与试题解析
一、选择题（本大题有10小题，每小题4分，共40分。请选出每小题中一个最符合题意的选项，不选、多选、错选均不给分）
1．实数2，0，﹣3，中，最小的数是（　　）
A．2 B．0 C．﹣3 D．
【分析】根据正数大于0，负数小于0，正数大于负数，即可判断出最小的数．
【解答】解：∵﹣3＜0＜＜2，
∴最小的数是﹣3，
故选：C．
2．第七次全国人口普查数据显示，绍兴市常住人口约为5270000人，这个数字5270000用科学记数法可表示为（　　）
A．0.527×107 B．5.27×106 C．52.7×105 D．5.27×107
【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，且n比原来的整数位数少1，据此判断即可．
【解答】解：5270000＝5.27×106．
故选：B．
3．如图的几何体由五个相同的小正方体搭成，它的主视图是（　　）

A． B． C． D．
【分析】根据从正面看得到的图形是主视图，可得答案．
【解答】解：从正面看，底层是三个小正方形，
故选：D．
4．在一个不透明的袋中装有6个只有颜色不同的球，其中3个红球、2个黄球和1个白球．从袋中任意摸出一个球，是白球的概率为（　　）
A． B． C． D．
【分析】用白球的数量除以所有球的数量即可求得白球的概率．
【解答】解：∵袋子中共有6个小球，其中白球有1个，
∴摸出一个球是白球的概率是，
故选：A．
5．如图，正方形ABCD内接于⊙O，点P在上（　　）

A．30° B．45° C．60° D．90°
【分析】根据正方形的性质得到BC弧所对的圆心角为90°，则∠BOC＝90°，然后根据圆周角定理求解．
【解答】解：连接OB、OC，

∵正方形ABCD内接于⊙O，
∴BC弧所对的圆心角为90°，
∴∠BOC＝90°，
∴∠BPC＝∠BOC＝45°．
故选：B．
6．关于二次函数y＝2（x﹣4）2+6的最大值或最小值，下列说法正确的是（　　）
A．有最大值4 B．有最小值4 C．有最大值6 D．有最小值6
【分析】根据题目中的函数解析式和二次函数的性质，可以得到该函数有最小值，最小值为6，然后即可判断哪个选项是正确的．
【解答】解：∵二次函数y＝2（x﹣4）2+6，a＝2＞2，
∴该函数图象开口向上，有最小值，
故选：D．
7．如图，树AB在路灯O的照射下形成投影AC，已知路灯高PO＝5m，树AB与路灯O的水平距离AP＝4.5m，则树的高度AB长是（　　）

A．2m B．3m C．m D．m
【分析】利用相似三角形的性质求解即可．
【解答】解：∵AB∥OP，
∴△CAB∽△CPO，
∴，
∴，
∴OP＝4（m），
故选：A．
8．如图，菱形ABCD中，∠B＝60°，沿折线BC﹣CD方向移动，移动到点D停止．在△ABP形状的变化过程中（　　）

A．直角三角形→等边三角形→等腰三角形→直角三角形
B．直角三角形→等腰三角形→直角三角形→等边三角形
C．直角三角形→等边三角形→直角三角形→等腰三角形
D．等腰三角形→等边三角形→直角三角形→等腰三角形
【分析】把点P从点B出发，沿折线BC﹣CD方向移动的整个过程，逐次考虑确定三角形的形状即可。
【解答】解：∵∠B＝60°，故菱形由两个等边三角形组合而成，
当AP⊥BC时，此时△ABP为等腰三角形；
当点P到达点C处时，此时△ABP为等边三角形；
当点P在CD上且位于AB的中垂线时，则△ABP为等腰三角形；
当点P与点D重合时，此时△ABP为等腰三角形，
故选：C．
9．如图，Rt△ABC中，∠BAC＝90°，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，连结CE，则的值为（　　）

A． B． C． D．2
【分析】设DE交AC于T,过点E作EH⊥CD于H.首先证明EA＝ED＝EC,再证明∠B＝∠ECD,可得结论。
【解答】解：设DE交AC于T,过点E作EH⊥CD于H．

∵∠BAC＝90°,BD＝DC,
∴AD＝DB＝DC,
∴∠B＝∠DAB,
∵∠B＝∠ADE,
∴∠DAB＝∠ADE,
∴AB∥DE,
∴∠DTC＝∠BAC＝90°,
∵DT∥AB,BD＝DC,
∴AT＝TC,
∴EA＝EC＝ED,
∴∠EDC＝∠ECD,
∵EH⊥CD,
∴CH＝DH,
∵DE∥AB,
∴∠EDC＝∠B,
∴∠ECD＝∠B,
∴cos∠ECH＝cosB＝,
∴＝,
∴＝＝2,
故选：D．
10．数学兴趣小组同学从“中国结”的图案（图1）中发现，用相同的菱形放置，用2个相同的菱形放置，得到3个菱形．下面说法正确的是（　　）

A．用3个相同的菱形放置，最多能得到6个菱形
B．用4个相同的菱形放置，最多能得到16个菱形
C．用5个相同的菱形放置，最多能得到27个菱形
D．用6个相同的菱形放置，最多能得到41个菱形
【分析】根据题意画出图形，从图形中找到出现的菱形的个数即可．
【解答】解：如图所示，
用2个相同的菱形放置，最多能得到3个菱形；
用8个相同的菱形放置，最多能得到8个菱形，
用4个相同的菱形放置，最多能得到16个菱形，
故选：B．
二、填空题（本大题有6小题，每小题5分，共30分）
11．（5分）分解因式：x2+2x+1＝　（x+1）2　．
【分析】本题中没有公因式，总共三项，其中有两项能化为两个数的平方和，第三项正好为这两个数的积的2倍，直接运用完全平方和公式进行因式分解．
【解答】解：x2+2x+8＝（x+1）2．
故答案为：（x+3）2．
12．（5分）我国明代数学读本《算法统宗》有一道题，其题意为：客人一起分银子，若每人7两；若每人9两，则差8两．银子共有　46　两．
【分析】通过设两个未知数，可以列出银子总数相等的二元一次方程组，本题得以解决．
【解答】解：设有x人，银子y两，
由题意得：，解得，
故答案为46．
13．（5分）图1是一种矩形时钟，图2是时钟示意图，时钟数字2的刻度在矩形ABCD的对角线BD上，则BC长为 　　cm（结果保留根号）．

【分析】根据题意即可求得∠FOD＝2∠DOE，即可求得∠DOE＝30°，由矩形的性质结合平行线的性质可求得∠DBC＝30°，利用含30° 角的直角三角形的性质可求解．
【解答】解：过O点作OE⊥CD，OF⊥AD，F，
由题意知∠FOD＝2∠DOE，

∵∠FOD+∠DOE＝90°，
∴∠DOE＝30°，∠FOD＝60°，
在矩形ABCD中，∠C＝90°，
∴OE∥BC，
∴∠DBC＝∠DOE＝30°，
∴BC＝CD＝，
故答案为．
14．（5分）如图，在△ABC中，AB＝AC，以点C为圆心，CA长为半径作弧，连结AP，则∠BAP的度数是　15°或75°　．

【分析】根据等腰三角形的性质可以得到△ABC各内角的关系，然后根据题意，画出图形，利用分类讨论的方法求出∠BAP的度数即可．
【解答】解：如右图所示，
当点P在点B的左侧时，
∵AB＝AC，∠ABC＝70°，
∴∠ACB＝ABC＝70°，
∴∠BAC＝180°﹣∠ACB﹣∠ABC＝180°﹣70°﹣70°＝40°，
∵CA＝CP1，
∴∠CAP1＝∠CP6A＝＝＝55°，
∴∠BAP1＝∠CAP1﹣∠CAB＝55°﹣40°＝15°；
当点P在点C的右侧时，
∵AB＝AC，∠ABC＝70°，
∴∠ACB＝ABC＝70°，
∴∠BAC＝180°﹣∠ACB﹣∠ABC＝180°﹣70°﹣70°＝40°，
∵CA＝CP4，
∴∠CAP2＝∠CP1A＝＝＝35°，
∴∠BAP2＝∠CAP2﹣∠CAB＝35°+40°＝75°；
由上可得，∠BAP的度数是15°或75°，
故答案为：15°或75°．

15．（5分）如图，在平面直角坐标系中，正方形ABCD的顶点A在x轴正半轴上，C在第一象限，顶点D的坐标（，2）（常数k＞0，x＞0）的图象恰好经过正方形ABCD的两个顶点，则k的值是　5或22.5　．

【分析】作DM⊥x轴于M，BN⊥轴于N，过C点作x轴的平行线，交DM于E，交BN于F，通过证得三角形求得表示出B、C的坐标，然后根据反比例函数系数k＝xy即可求得结果．
【解答】解：作DM⊥x轴于M，BN⊥轴于N，交DM于E，
正方形ABCD中，∠BAD＝90°，
∴∠DAM+∠BAN＝90°，
∵∠ADM+∠DAM＝90°，
∴∠ADM＝∠BAN，
在△ADM和△BAN中，
，
∴△ADM≌△BAN（AAS），
∴AM＝BN，DM＝AN，
∵顶点D的坐标（，6）．
∴OM＝，DM＝6，
同理：△ADM≌△DCE，
∴AM＝DE，CE＝DM，
∴AM＝BN＝DE，DM＝AN＝CE＝2，
设AM＝BN＝DE＝m，
∴ON＝+m+2＝4.5+m，
∴B（4.5+m，m），4+m），
当反比例函数y＝（常数k＞0、D时×2＝5；
当反比例函数y＝（常数k＞5、c时，
解得m＝3，
∴k＝4.7×（2+3）＝22.6，
故答案为5或22.5．

16．（5分）已知△ABC与△ABD在同一平面内，点C，D不重合，AB＝4，AC＝AD＝2　2±2或4或2　．
【分析】分C,D在AB的同侧或异侧两种情形，分别求解，注意共有四种情形。
【解答】解：如图，当C，过点A作AE⊥CD于E．

在Rt△AEB中，∠AEB＝90°,∠ABE＝30°,
∴AE＝AB＝5,
∵AD＝AC＝2,
∴DE＝＝2＝2,
∴DE＝EC＝AE,
∴△ADC是等腰直角三角形，
∴CD＝5,
当C,D异侧时,
∵△BCC′是等边三角形，BC＝BE﹣EC＝2,
∴CH＝BH＝﹣1CH＝3﹣2,
在Rt△DC′H中，DC′＝＝,
∵△DBD′是等边三角形，
∴DD′＝2+6,
∴CD的长为2±7或4或2。
故答案为：2±8或4或2。
三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题8分，第24小题14分，共80分.解答需写出必要的文字说明、演算步骤或证明过程
17．（8分）（1）计算：4sin60°﹣+（2﹣）0．
（2）解不等式：5x+3≥2（x+3）．
【分析】（1）原式第一项利用特殊角的三角函数值计算，第二项利用开平方法则化简，最后一项利用零指数幂的意义化简，计算即可得到结果；
（2）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项，系数化为1可得．
【解答】解：（1）原式＝2﹣6
＝1；
（2）8x+3≥2（x+4），
去括号得：5x+3≥5x+6,
移项得：5x﹣5x≥6﹣3，
合并同类项得：6x≥3，
解得：x≥1．
18．（8分）绍兴莲花落，又称“莲花乐”，“莲花闹”，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，并将抽查结果绘制成不完整的统计图．

根据图中信息，解答下列问题：
（1）本次接受问卷调查的学生有多少人？并求图2中“了解”的扇形圆心角的度数；
（2）全校共有1200名学生，请你估计全校学生中“非常了解”、“了解”莲花落的学生共有多少人．
【分析】（1）从两个统计图中可知，在抽查人数中，“非常了解”的人数为30人，占调查人数的15%，可求出接受问卷调查的学生数，进而求出“了解”所占比例，即可得出“了解”的扇形圆心角的度数；
（2）样本中“非常了解”、“了解”的占调查人数的，进而估计总体中“非常了解”和“了解”的人数．
【解答】解：（1）接受问卷调查的学生数：30÷15%＝200（人），
“了解”的扇形圆心角度数为360°×＝126°；
答：本次接受问卷调查的学生有200人，图2中“了解”的扇形圆心角的度数为126°；

（3）1200×＝600（人），
答：估计全校学生中“非常了解”、“了解”莲花落的学生共有600人．
19．（8分）Ⅰ号无人机从海拔10m处出发，以10m/min的速度匀速上升，Ⅱ号无人机从海拔30m处同时出发（m/min）的速度匀速上升，经过5min两架无人机位于同一海拔高度b（m）（m）与时间x（min）的关系如图．两架无人机都上升了15min．
（1）求b的值及Ⅱ号无人机海拔高度y（m）与时间x（min）的关系式；
（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

【分析】（1）由题意得：b＝10+10×5＝60；再用待定系数法求出函数表达式即可；
（2）由题意得：（10z+10）﹣（6x+30）＝28，即可求解．
【解答】解：（1）b＝10+10×5＝60，
设函数的表达式为y＝kx+t，
将（0,30）,60）代入上式得，
故函数表达式为y＝6x+30（5≤x≤15）；

（2）由题意得：（10z+10）﹣（6x+30）＝28，
解得x＝12＜5，
故无人机上升12min，Ⅰ号无人机比Ⅱ号无人机高28米．
20．（8分）拓展小组研制的智能操作机器人，如图1，水平操作台为l，高AB为50cm，连杆BC长度为70cm，C是转动点，且AB
（1）转动连杆BC，手臂CD，使∠ABC＝143°，如图2，求手臂端点D离操作台l的高度DE的长（精确到1cm，参考数据：sin53°≈0.8，cos53°≈0.6）．
（2）物品在操作台l上，距离底座A端110cm的点M处，转动连杆BC，手臂端点D能否碰到点M？请说明理由．

【分析】（1）过点C作CP⊥AE于点P，过点B作BQ⊥CP于点Q，在Rt△BCQ中，CQ＝BC•sin53°，再根据DE＝CP＝CQ+PQ可得答案；
（2）当B,C,D共线时，根据勾股定理可得AD的长，进而可进行判断．
【解答】解：（1）过点C作CP⊥AE于点P，过点B作BQ⊥CP于点Q

∵∠ABC＝143°，
∴∠CBQ＝53°，
在Rt△BCQ中，CQ＝BC•sin53°≈70×0.8＝56cm，
∵CD∥l，
∴DE＝CP＝CQ+PQ＝56+50＝106cm．
（2）当B,C,D共线时

BD＝60+70＝130cm，AB＝50cm，
在Rt△ABD中，AB²+AD²＝BD²，
∴AD＝120cm＞110cm．
∴手臂端点D能碰到点M．
21．（10分）如图，在△ABC中，∠A＝40°，E分别在边AB，AC上，连结CD，BE．
（1）若∠ABC＝80°，求∠BDC，∠ABE的度数；
（2）写出∠BEC与∠BDC之间的关系，并说明理由．

【分析】（1）根据等腰三角形的性质得到∠BDC＝∠BCD＝(180°﹣80°)＝50°,根据三角形的内角定理得到∠ACB＝180°﹣40°﹣50°＝60°,推出△BCE是等边三角形，得到∠EBC＝60°,于是得到结论;
(2)设∠BEC＝α,∠BDC＝β,由于α＝∠A+∠ABE＝40°+∠ABE,根据等腰三角形的性质得到∠CBE＝∠BEC＝α,求得∠ABC＝∠ABE+∠CBE＝∠A+2∠ABE＝40°+∠ABE,推出∠CBE＝∠BEC＝α,于是得到结论。
【解答】解：（1）∵∠ABC＝80°，BD＝BC,
∴∠BDC＝∠BCD＝(180°﹣80°)＝50°,
∵∠A+∠ABC+∠ACB＝180°,∠A＝40°,
∴∠ACB＝180°﹣40°﹣50°＝60°,
∵CE＝BC,
∴△BCE是等边三角形，
∴∠EBC＝60°,
∴∠ABE＝∠ABC﹣∠EBC＝20°;
(2)∠BEC与∠BDC之间的关系：∠BEC+∠BDC＝110°,
理由：设∠BEC＝α,∠BDC＝β,
在△ABE中，α＝∠A+∠ABE＝40°+∠ABE,
∵CE＝BC,
∴∠CBE＝∠BEC＝α,
∴∠ABC＝∠ABE+∠CBE＝∠A+4∠ABE＝40°+∠ABE,
∵CE＝BC,
∴∠CBE＝∠BEC＝α,
∴∠ABC＝∠ABE+∠CBE＝∠A+2∠ABE＝40°+2∠ABE,
在△BDC中，BD＝BC,
∴∠BDC+∠BCD+∠DBC＝6β+40°+2∠ABE＝180°,
∴β＝70°﹣∠ABE,
∴α+β＝40°+∠ABE+70°﹣∠ABE＝110°,
∴∠BEC+∠BDC＝110°．
22．（12分）小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，杯体ACB是抛物线的一部分，抛物线的顶点C在y轴上，且点A，B关于y轴对称，杯高DO＝8，杯底MN在x轴上．
（1）求杯体ACB所在抛物线的函数表达式（不必写出x的取值范围）；
（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯口直径A′B′∥AB，杯脚高CO不变，求A′B′的长．

【分析】（1）运用待定系数法，由题意设顶点式y＝ax2+4，进而求得答案；
（2）由题意知：＝0.6，进而求得OD′＝10，再由题意得抛物线y＝x2+4过B′(x1,10),A′(x2,10),从而列方程求出x1 和x2，进而求得A′B′的长．
【解答】解：（1）∵CO＝4，
∴顶点C(0，8)，
∴设抛物线的函数表达式为y＝ax2+4，
∵AB＝6，
∴AD＝DB＝2，
∵DO＝8，
∴A(﹣7，8)，8)，
将B(5，8)代入y＝ax2+5，
得：8＝a×22+4，
解得：a＝1，
∴该抛物线的函数表达式为y＝x2+4；
（2）由题意得：＝0.6,
∴＝0.3，
∴CD′＝6，
∴OD′＝OC+CD′＝4+2＝10，
又∵杯体A′CB′所在抛物线形状不变，杯口直径A′B′∥AB，
∴设B′(x1，10)，A′(x2，10),
∴当y＝10时，10＝x7+4，
解得：x1＝，x2＝﹣，
∴A′B′＝4，
∴杯口直径A′B′的长为2．
23．（12分）问题：如图，在▱ABCD中，AB＝8，∠DAB，∠ABC的平分线AE，F，求EF的长．
答案：EF＝2．
探究：（1）把“问题”中的条件“AB＝8”去掉，其余条件不变．
①当点E与点F重合时，求AB的长；
②当点E与点C重合时，求EF的长．
（2）把“问题”中的条件“AB＝8，AD＝5”去掉，其余条件不变，D，E，F相邻两点间的距离相等时，求的值．

【分析】（1）①证∠DEA＝∠DAE，得DE＝AD＝5，同理BC＝CF＝5，即可求解；
②由题意得DE＝DC＝5，再由CF＝BC＝5，即可求解；
（2）分三种情况，由（1）的结果结合点C，D，E，F相邻两点间的距离相等，分别求解即可．
【解答】解：（1）①如图1所示：

∵四边形ABCD是平行四边形，
∴CD＝AB＝8，BC＝AD＝5，
∴∠DEA＝∠BAE，
∵AE平分∠DAB，
∴∠DAE＝∠BAE，
∴∠DEA＝∠DAE，
∴DE＝AD＝5，
同理：BC＝CF＝5，
∵点E与点F重合，
∴AB＝CD＝DE+CF＝10；
②如图3所示：

∵点E与点C重合，
∴DE＝DC＝5，
∵CF＝BC＝5，
∴点F与点D重合，
∴EF＝DC＝5；
（2）分三种情况：
①如图3所示：

同（1）得：AD＝DE，
∵点C，D，E，F相邻两点间的距离相等，
∴AD＝DE＝EF＝CF，
∴＝；
②如图4所示：

同（1）得：AD＝DE＝CF，
∵DF＝FE＝CE，
∴＝；
③如图5所示：

同（1）得：AD＝DE＝CF，
∵DF＝DC＝CE，
∴＝2；
综上所述，的值为或．
24．（14分）如图，矩形ABCD中，AB＝4，点F是对角线BD上一动点，∠ADB＝30°．连结EF
（1）若EF⊥BD，求DF的长；
（2）若PE⊥BD，求DF的长；
（3）直线PE交BD于点Q，若△DEQ是锐角三角形，求DF长的取值范围．

【分析】（1）由题意得点P在BD上，根据含30°直角三角形的性质即可求解；
（2）由对称可得△DEF是等腰三角形，分两种情况画出图形，根据含30°直角三角形的性质即可求解；
（3）分两种情况画出图形，根据中点的定义以及直角三角形的性质分别求出EM、FM、DM的值，即可得出DF的值，结合（2）中求得的DF的值即可得出答案。
【解答】解：（1）∵点D、点P关于直线EF的对称，
∴点P在BD上，

∵四边形ABCD是矩形，
∴∠BAD＝90°，
∵AB＝4，∠ADB＝30°．
∴AD＝4，
∵点E是边AD的中点，
∴DE＝2，
∵EF⊥BD，
∴DF＝8；
（2）①如图2，

∵PE⊥BD，∠ADB＝30°．
∴∠PED＝60°,
由对称可得，EF平分∠PED，
∴∠DEF＝∠PEF＝30°，
∴△DEF是等腰三角形，
∴DF＝EF,
∵PE⊥BD,∠ADB＝30°，
∴QE＝,
∵∠PEF＝30°，
∴EF＝2,
∴DF＝EF＝2；
②如图5，

∵PE⊥BD，∠ADB＝30°．
∴∠PED＝120°,
由对称可得，PF＝DF,EF平分∠PED，
∴∠DEF＝∠PEF＝120°，
∴∠EFD＝30°,
∴△DEF是等腰三角形，
∵PE⊥BD,
∴QD＝QF＝DF,
∵PE⊥BD,∠ADB＝30°，
∴QE＝,QD＝3
∴DF＝7QD＝6；
∴DF的长为2或6；
（3）由（2）得，当∠DQE＝90°时,
当∠DEQ＝90°时，
第一种情况，如图4，

∵EF平分∠PED,
∴∠DEF＝45°,
过点F作FM⊥AD于点M，设EM＝a,DM＝a，
∴a+a＝2，
∴a＝8﹣,DF＝6﹣8,
∴2<DF<；
第二种情况,如图5,

∵EF平分∠AEQ,
∴∠MEF＝45°,
过点F作FM⊥AD于点M，设EM＝a,DM＝a，
∴a﹣a＝2，
∴a＝5+,DF＝6+6,
∵6+5＞8,
∴DF最大值为5，
∴6<DF≤8。
综上，DF长的取值范围为3<<6﹣2<DF≤8．