高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式课文配套ppt课件

这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.3 诱导公式课文配套ppt课件，共33页。
1.借助单位圆的对称性,利用定义推导出诱导公式(α±π的正弦、余弦、正切),并熟练掌握.2.能运用有关诱导公式解决一些三角函数的化简、求值和证明问题.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
目 录 索 引
知识点 诱导公式二、三、四
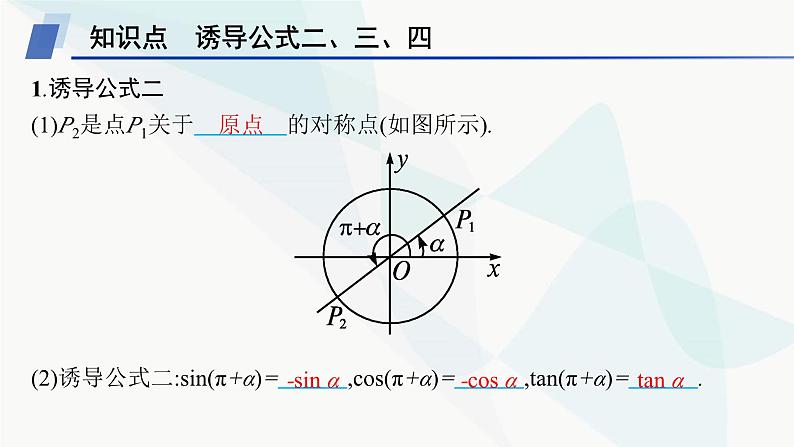
1.诱导公式二(1)P2是点P1关于　　　　的对称点(如图所示). (2)诱导公式二:sin(π+α)=　　　,cs(π+α)=　　　,tan(π+α)=　　 . 
2.诱导公式三(1)P2是点P1关于　　的对称点(如图所示). (2)诱导公式三:sin(-α)=　 　　,cs(-α)=　 　　,tan(-α)=　　　　. 
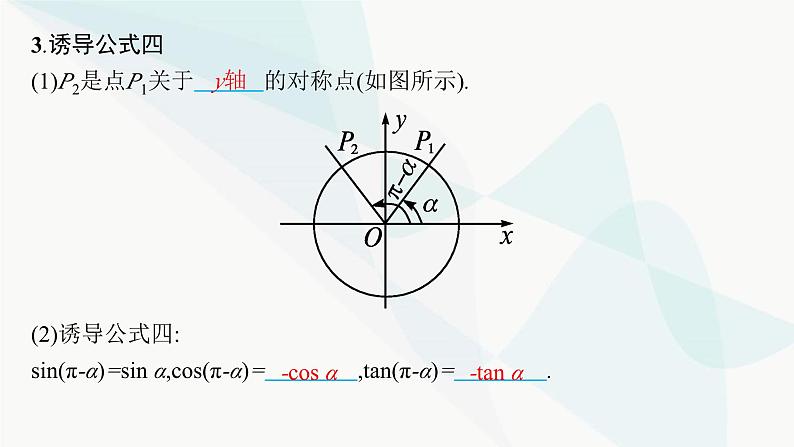
3.诱导公式四(1)P2是点P1关于　　　的对称点(如图所示). (2)诱导公式四:sin(π-α)=sin α,cs(π-α)=　　　　,tan(π-α)=　　　　. 
名师点睛1.公式一至四的概念:α+k·2π(k∈Z),-α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.2.判断函数值的符号时,虽然把α看成锐角,但实际上,对于正弦与余弦的诱导公式,α可以为任意角;对于正切的诱导公式,α的终边不能落在y轴上,即α≠kπ+ (k∈Z).3.公式既可以用弧度制表示,也可以用角度制表示.
过关自诊1.公式四除了利用π-α的终边与α的终边关于y轴对称推导外,还可以如何推导?
2.如何理解“函数名不变,符号看象限”?
提示 借助公式二、三,如:sin(π-α)=sin[π+(-α)]=-sin(-α)=sin α.
提示 “函数名不变”是指等式两边的三角函数同名;“符号看象限”是指把原角看成锐角时新角在原函数下的符号,由新角所在象限确定符号.如sin(π+α),若把α看成锐角,则π+α在第三象限,所以取负号,故sin(π+α)=-sin α.
3.下列式子中正确的是(　　)A.sin(π-α)=-sin αB.cs(π+α)=cs αC.cs α=sin αD.sin(2π+α)=sin α
4.已知tan α=6,则tan(-α)=　　　　　. 
对于选项B,令α=0,得cs(π+α)=cs π=-1≠cs 0,所以B错误;对于选项C,令α=0,得cs α=cs 0=1≠sin 0,所以C错误;易知D正确.
5.[北师大版教材例题]画出下列各组中的两个角的终边与单位圆的交点,说出它们的对称关系.
探究点一　给角求值问题
(2)cs(-2 040°)=　　　　　　. 
规律方法　利用诱导公式解决给角求值问题的基本步骤
(2)tan 10°+tan 170°+sin 1 866°-sin(-606°).
解 原式=tan 10°+tan(180°-10°)+sin(5×360°+66°)-sin[(-2)×360° +180°-66°]=tan 10°-tan 10°+sin 66°-sin(180°-66°)=sin 66°-sin 66°=0.
探究点二　给值(式)求值问题
【例2】 (1)若cs 165°=a,则tan 195°=(　　)
规律方法　解决给值(式)求值问题的策略(1)解决给值(式)求值问题,首先要仔细观察条件式与所求式之间的角、函数名称及有关运算之间的差异及联系.(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.
变式训练2 已知tan 100°=k,则sin 80°的值等于(　　)
解析 由题意tan 100°=k=tan(180°-80°)=-tan 80°,
探究点三　三角函数的化简求值问题
规律方法　利用诱导公式一至四化简应注意的问题(1)利用诱导公式主要是进行角的转化,从而达到统一角的目的.(2)化简时函数名不发生改变,但要注意函数的符号有没有改变.(3)同时有切(正切)与弦(正弦、余弦)的式子化简,一般采用切化弦,有时也可以弦化切.
解析 因为tan(5π+α)=tan(π+α)=tan α=m,
本节要点归纳1.知识清单:(1)特殊关系角的终边对称性.(2)诱导公式二~四.2.方法归纳:公式法、角变换、化归思想.3.常见误区:符号的确定.
1.tan(-600°)的值等于(　　)
解析 tan(-600°)=-tan 600°=-tan(360°+240°)=-tan 240°=-tan(180°+60°)=-tan 60°=- .
5.已知600°角的终边上有一点P(a,-3),则实数a的值为　　　　　.