





人教A版 (2019)2.3 二次函数与一元二次方程、不等式作业课件ppt
展开A.{x|-6≤x≤1}B.{x|x≥1,或x≤-6}C.{x|-6≤x<1}D.{x|x>1,或x≤-6}
故解集为{x|-6≤x<1}.
2.[探究点一·2023陕西宝鸡质检]若集合A={x|(2x+1)(x-3)<0}, B={x|x∈N*,x≤5},则A∩B等于( )A.{1,2,3}B.{1,2}C.{4,5}D.{1,2,3,4,5}
解析 ∵(2x+1)(x-3)<0,∴-
4.[探究点二(角度3)]若不等式ax2+ax+a+3≥0对一切实数x恒成立,则实数a的取值范围是( )A.{a|-4
解析 由不等式ax2+bx+c≥0的解集是{x|-1≤x≤2}可得a<0,且方程ax2+bx+c=0的两个根为-1,2,所以- =-1+2=1>0,所以b=-a,b>0,故A正确,D错误;由 =-2,则c>0,故C正确;依题意二次函数y=ax2+bx+c的图象开口向下,且二次函数的图象与x轴的两个交点横坐标是-1,2,因此当x=1时,y=a+b+c>0,故B正确.故选ABC.
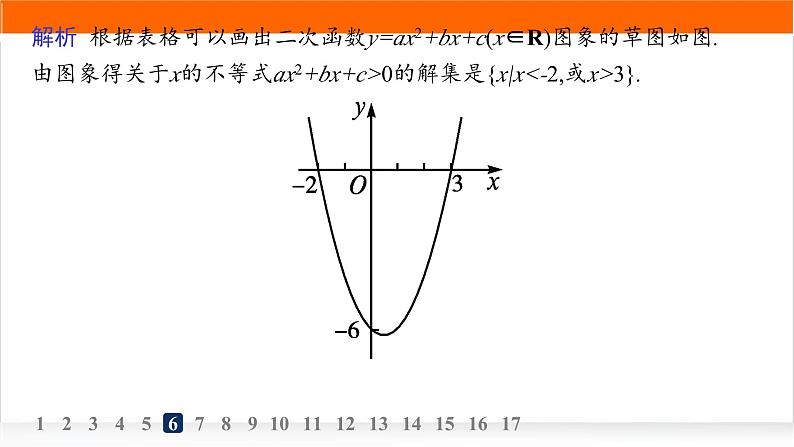
6.[探究点二(角度2)]二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
则关于x的不等式ax2+bx+c>0的解集是 .
{x|x<-2,或x>3}
解析 根据表格可以画出二次函数y=ax2+bx+c(x∈R)图象的草图如图.由图象得关于x的不等式ax2+bx+c>0的解集是{x|x<-2,或x>3}.
7.[探究点二(角度3)·2023吉林梅河口期末]若关于x的不等式(m-1)x2+(m-1)x+2>0的解集为R,则实数m的取值范围是 .
8.[探究点三]某产品的总成本y(单位:万元)与产量x(单位:台)之间的函数关系是y=3 000+20x-0.1x2(0
10.若关于x的不等式x2-(m+2)x+2m<0的解集中恰有4个正整数,则实数m的取值范围为( )A.{m|6
解析 原不等式可化为(x-2)(x-m)<0,若m<2,则解得m
解析 当a=0时,不等式ax2+x-(a+1)=x-1≥0,解得x≥1,不满足题意;当a≠0时,由于不等式ax2+x-(a+1)≥0的解集是{x|-2≤x≤1}的子集,则a<0,解方程ax2+x-(a+1)=0,
故AD选项满足题意,BC选项不满足题意.故选AD.
13.若1≤x≤2时,不等式x2+mx+m≥0恒成立,则实数m的最小值为 .
解析 令y=x2+mx+m,若1≤x≤2时,不等式x2+mx+m≥0恒成立,
14.已知不等式ax2-3x+6>4的解集为{x|x<1,或x>b}.(1)求a,b的值;(2)解不等式ax2-(ac+b)x+bc<0.
解 (1)因为不等式ax2-3x+6>4的解集为{x|x<1,或x>b},所以x1=1与x2=b是方程ax2-3x+2=0的两个实数根,b>1且a>0.
(2)由(1)知不等式ax2-(ac+b)x+bc<0可化为x2-(2+c)x+2c<0,即(x-2)(x-c)<0.当c>2时,不等式(x-2)(x-c)<0的解集为{x|2
解 A={x|x2-4x+3≤0}={x|1≤x≤3},若“x∈A”是“x∈B”的必要不充分条件,则集合B是集合A的真子集,
解析 原不等式等价于x(x-1)-(a-2)(a+1)≥1,即x2-x-1≥(a+1)(a-2)对任意x恒成立.
17.已知关于x的不等式(kx-k2-4)(x-4)>0的解集为A,其中k∈R.(1)若5∈A,求实数k的取值范围.(2)求不等式的解集A.(3)是否存在实数k,使得上述不等式的解集A中只有有限个整数?若存在,求出使得A中整数个数最少的k的值;若不存在,请说明理由.
解 (1)由题意(5k-k2-4)(5-4)>0,解得1
高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式作业ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式作业ppt课件,共11页。PPT课件主要包含了aa1等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册2.2 基本不等式作业ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册2.2 基本不等式作业ppt课件,共15页。PPT课件主要包含了BCD,ABC,ABD等内容,欢迎下载使用。
人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式备课课件ppt: 这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式备课课件ppt,共39页。PPT课件主要包含了目录索引等内容,欢迎下载使用。













