人教A版 (2019)选择性必修 第二册4.2 等差数列集体备课课件ppt

这是一份人教A版 (2019)选择性必修 第二册4.2 等差数列集体备课课件ppt，共35页。PPT课件主要包含了目录索引，本节要点归纳等内容，欢迎下载使用。
1.能够根据等差数列的定义和通项公式推出等差数列的重要性质.2.能够运用等差数列的性质解决有关问题.3.能够运用等差数列的知识解决简单的实际问题.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
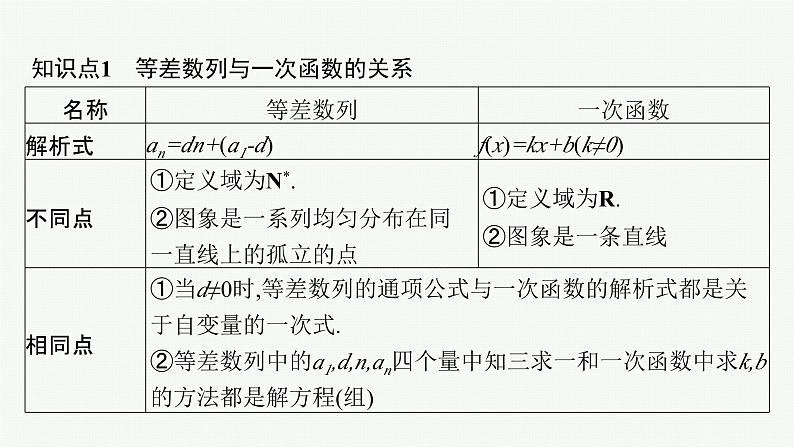
知识点1　等差数列与一次函数的关系
过关自诊1.[人教B版教材习题]根据下列等差数列的通项公式,求数列的首项与公差.(1)an=3n+5;(2)an=12-2n.
解 (1)a1=3×1+5=8,a2=3×2+5=11,公差d=a2-a1=11-8=3.(2)a1=12-2×1=10,a2=12-2×2=8,公差d=8-10=-2.
2.[北师大版教材习题]已知等差数列的通项公式为an=-2n+7.(1)求首项a1和公差d;(2)画出数列{an}的图象;(3)判断数列{an}的单调性.
解 (1)a1=-2×1+7=5,a2=-2×2+7=3,d=a2-a1=3-5=-2.
(2){an}的图象如图所示.
(3)由(1)知d1,且n∈N*.(　　)
2.[人教B版教材习题]如果{an}是等差数列,而且正整数s,t,p,q满足s+t=p+q,求证:as+at=ap+aq.
证明设等差数列{an}的首项和公差分别为a1,d.则as=a1+(s-1)d,at=a1+(t-1)d,ap=a1+(p-1)d,aq=a1+(q-1)d.∴as+at=2a1+(s+t-2)d,ap+aq=2a1+(p+q-2)d.又s+t=p+q,∴as+at=ap+aq.
探究点一　等差数列性质的应用
【例1】 (1)已知等差数列{an},a5=10,a15=25,求a25的值.分析 根据各个题的特征,选择相应等差数列的性质求解.
(方法2)因为5+25=2×15,所以在等差数列{an}中有a5+a25=2a15,从而a25=2a15-a5=2×25-10=40.(方法3)因为5,15,25成等差数列,所以a5,a15,a25也成等差数列,因此a25-a15=a15-a5,即a25-25=25-10,解得a25=40.
(2)已知等差数列{an},a3+a4+a5+a6+a7=70,求a1+a9的值.
解 由等差数列的性质,得a3+a7=a4+a6=2a5=a1+a9,所以a3+a4+a5+a6+a7=5a5=70,于是a5=14,故a1+a9=2a5=28.
(3)已知数列{an},{bn}都是等差数列,且a1=2,b1=-3,a7-b7=17,求a19-b19的值.
解 令cn=an-bn,因为{an},{bn}都是等差数列,所以{cn}也是等差数列,设其公差为d,由已知,得c1=a1-b1=5,c7=17,则5+6d=17,解得d=2,故a19-b19=c19=5+18×2=41.
规律方法　求等差数列基本运算的两种方法一是利用基本量运算,借助于a1,d建立方程组进行运算,这是最基本的方法;二是利用性质运算,运用等差数列的性质可简化计算,往往会有事半功倍的效果.
变式训练1(1)在等差数列{an}中,已知a3+a8=10,则3a5+a7=　　　　　. 
解析 由已知得3a5+a7=2a5+(a5+a7)=2a5+2a6=2(a3+a8)=20.
(2)设等差数列{an}满足a1+a3+a5=9.①求a3;②若a1+a2+a3,a4+a5+a6,a7+a8+a9是公差为18的等差数列,求数列{an}的通项公式.
解 ①在等差数列{an}中,a1+a3+a5=3a3=9,所以a3=3.②设等差数列{an}的公差为d,因为a1+a2+a3,a4+a5+a6,a7+a8+a9是公差为18的等差数列,所以3a2,3a5,3a8是公差为18的等差数列,所以a8-a5=3d=6,所以d=2,所以an=a3+(n-3)d=3+2(n-3)=2n-3.
探究点二　等差数列的综合问题
【例2】 (1)设{an}是公差为正数的等差数列,若a1+a2+a3=15,a1a2a3=80,求a11+a12+a13的值.
分析 由于已知条件中含等差数列前3项的和与积,因此可考虑利用等差中项及等差数列性质求解
解 设{an}的公差为d,∵a1+a3=2a2,∴a1+a2+a3=15=3a2,∴a2=5.又a1a2a3=80,{an}是公差为正数的等差数列,∴a1a3=(5-d)(5+d)=16,解得d=3或d=-3(舍去),∴a12=a2+10d=35,∴a11+a12+a13=3a12=105.
(2)已知四个数依次成等差数列,且是递增数列,这四个数的平方和为94,首尾两数之积比中间两数之积少18,求此等差数列.
分析 涉及四个数成等差数列,因此可考虑用“对称性”设出这四个数.
解 设这四个数分别为a-3d,a-d,a+d,a+3d,则
规律方法　等差数列设未知量的技巧如下:(1)当等差数列{an}的项数n为奇数时,可先设中间一项为a,再用公差为d向两边分别设项:…,a-2d,a-d,a,a+d,a+2d,….(2)当等差数列{an}的项数n为偶数时,可先设中间两项为a-d,a+d,再以公差为2d向两边分别设项:…,a-3d,a-d,a+d,a+3d,….这种设法称为对称项设法,这样可减少计算量.
变式训练2已知三个数成等差数列,且数列是递增数列,它们的和为18,平方和为116,求这三个数.
解 (方法1)由题意设这三个数分别为a,b,c,a