人教A版高中数学必修第一册第3章一元二次函数、方程和不等式3-2-1第1课时函数的单调性课件

这是一份人教A版高中数学必修第一册第3章一元二次函数、方程和不等式3-2-1第1课时函数的单调性课件，共40页。

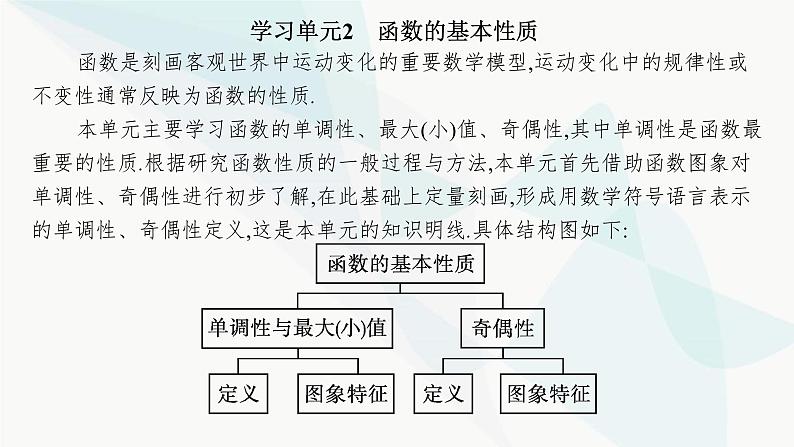
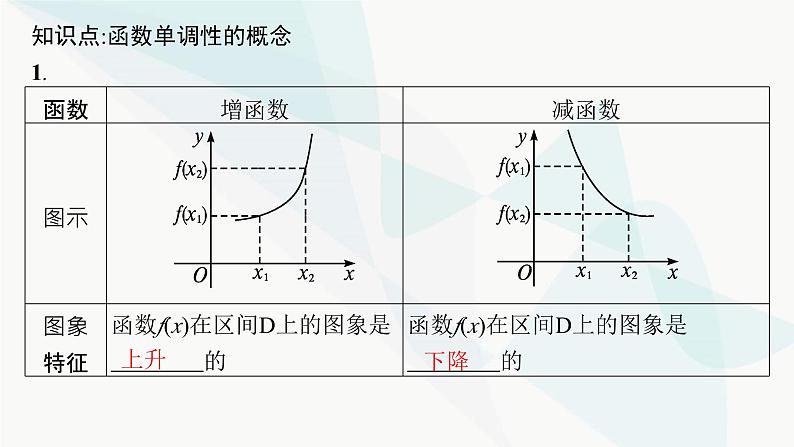
第三章3.2.1　第2课时　函数的最大(小)值基础落实·必备知识全过关重难探究·能力素养全提升目录索引 学以致用·随堂检测全达标函数是刻画客观世界中运动变化的重要数学模型,运动变化中的规律性或不变性通常反映为函数的性质.本单元主要学习函数的单调性、最大(小)值、奇偶性,其中单调性是函数最重要的性质.根据研究函数性质的一般过程与方法,本单元首先借助函数图象对单调性、奇偶性进行初步了解,在此基础上定量刻画,形成用数学符号语言表示的单调性、奇偶性定义,这是本单元的知识明线.具体结构图如下:学习单元2　函数的基本性质 学习过程中,通过“什么是函数的性质”“如何研究函数性质”等体现数学基本思想的问题,引导数学思维的发散.总体来说,既体现研究数学性质的一般思路,又注意函数性质的特殊性——变化中的规律性、不变性.研究方法上,通过代数运算和图象直观揭示函数的性质;构建从具体到抽象、从特殊到一般的过程,归纳概括单调性的方法,培养数形结合思想,提升数学运算、直观想象等素养.基础落实·必备知识全过关知识点:函数单调性的概念1.上升 下降<> 不同区间用逗号隔开2.如果函数y=f(x)在区间D上单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)　　　　　,区间　　　　叫做y=f(x)的单调区间. 单调性D名师点睛1.函数的单调性是函数在某个区间上的性质,是一个局部特征,不同的单调区间用逗号隔开.2.对于某一个点,由于它的函数值是唯一确定的常数,没有增减变化,所以不存在单调性问题,因此在书写单调区间时,可以包括端点,也可以不包括端点,但在某些点无意义时,单调区间不能包括这些点.3.单调性定义还可以用如下的代数方式表示:单调递增:区间D中任意x1≠x2,有(x1-x2)[f(x1)-f(x2)]>0;单调递减:区间D中任意x1≠x2,有(x1-x2)[f(x1)-f(x2)]<0.微思考已知四个函数的图象如图所示,其中在定义域内具有单调性的函数是哪个?提示 在定义域内任取的两个自变量与相应函数值的关系满足单调性定义,故只有B选项的图象满足.重难探究·能力素养全提升问题1单调性是函数的重要性质.通过单调性容易知道函数图象趋势,数形结合,从而解决函数的众多问题.如何确定函数的单调性呢?探究点一 确定函数的单调区间问题2对于熟悉的函数,如何确定它们的单调区间?【例1】 (1)下列函数中,在(0,+∞)上单调递增的是(　　)A.f(x)=3-x B.f(x)=x2-3xC.f(x)=- D.f(x)=-|x|C解析函数f(x)=3-x为一次函数,在(0,+∞)上单调递减,不符合题意;函数f(x)=x2-3x为二次函数,在 上单调递减,不符合题意;函数f(x)=- 为反比例函数,在(0,+∞)上单调递增,符合题意;函数f(x)=-|x|,当x>0时,f(x)=-x,则函数f(x)在(0,+∞)上单调递减,不符合题意.故选C.(2)函数y=x2-2|x|+1的单调递增区间是(　　)A.(-1,0) B.(-1,0)和(1,+∞) C.(-∞,-1) D.(-∞,-1)和(0,1)B解析由题得, 作出函数图象如图所示,由函数图象可知,函数的单调递增区间为(-1,0)和(1,+∞).故选B.延伸探究已知x∈R,函数f(x)=x|x-2|,试画出y=f(x)的图象,并结合图象写出函数的单调区间.解 f(x)=x|x-2|= 图象如图所示.由图象可知,函数的单调递增区间为(-∞,1],[2,+∞);单调递减区间为[1,2].规律方法　1.一次函数、二次函数及反比例函数的单调性.(1)一次函数y=kx+b(k≠0)的单调性由系数k决定:当k>0时,该函数在R上是增函数;当k<0时,该函数在R上是减函数.(2)二次函数y=ax2+bx+c(a≠0)的单调性以对称轴x=- 为分界线.(3)反比例函数y= (k≠0)的单调性如下表所示. 2.对于含绝对值的函数可以去掉绝对值号转化为分段函数或作出函数图象判断函数单调性.探究点二 证明函数的单调性问题3对于不熟悉的函数,如何确定区间上的单调性?问题4单调性的几何特征可否用代数形式来刻画?如何表示?还可以如何变形?问题5如何用代数方式证明函数的单调性?【例2】 求证:函数f(x)=x+ 在区间(0,1)上单调递减. 规律方法　1.利用定义法证明或判断函数的单调性的步骤 2.作差变形的常用技巧(1)因式分解.当原函数是多项式函数时,作差后的变形通常进行因式分解.如f(x)=x2-2x-3=(x-3)(x+1).(2)通分.当原函数是分式函数时,作差后往往进行通分,然后对分子进行因式分解.如本例.(3)配方.当所得的差式是含有x1,x2的二次三项式时,可以考虑配方,便于判断符号.(4)分子有理化.当原函数是根式函数时,作差后往往考虑分子有理化.探究点三 函数单调性的应用问题6函数单调性可以用来解决哪些问题?对于正向的问题如何进行适当的逆向思考?1.根据函数单调性比较大小【例3】 已知f(x)是定义在(0,+∞)上的减函数,试比较f(a2-a+1)与f( )的大小.规律方法　函数单调性的应用问题的解题策略(1)利用函数的单调性可以比较函数值或自变量的大小.利用函数的单调性解决比较函数值大小的问题时,要注意将对应的自变量转化到同一个单调区间上.(2)利用函数的单调性解函数值的不等式就是利用函数在某个区间内的单调性,去掉对应关系“f”,转化为自变量的不等式,此时一定要注意自变量的限制条件,以防出错.2.根据函数单调区间或单调性求参数范围【例4】 函数f(x)=x2+(2a+1)x+1在区间[1,2]上单调,则实数a的取值范围是(　　)A 规律方法　含参数的函数单调性问题,应明确若函数在某一区间M上是单调递增(或单调递减),则该区间是函数的原单调递增区间(或单调递减区间)D的子集,即M⊆D.3.分段函数的单调性问题7分段函数的单调性如何理解?如何说明分段函数是定义域上的单调函数?【例5】 (多选题)已知分段函数 的定义域为R,且满足对于任意的x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,则a的可能取值是(　　)A.1 B.-1 C.-2 D.-3CD规律方法　由于分段函数是一个函数,因此对于分段函数在实数集R上的单调递增(减)的问题,除了保证在定义域的每一个区间上单调性相同之外,还要考虑在分界点处的函数值的大小应满足函数的单调性,否则求出的参数的范围会出现错误.探究点四 复合函数的单调性问题8复合函数的单调性如何判断?【例6】 试求函数 的单调区间.解由题意可知,g(x)的定义域为{x|x≠-2,且x≠4}.令u(x)=8+2x-x2,则u(x)在(-∞,-2),(-2,1]上单调递增,在[1,4),(4,+∞)上单调递减.函数g(u)= 在(-∞,0)和(0,+∞)上分别单调递减.根据复合函数“同增异减”的原则,可知g(x)= 在区间(-∞,-2),(-2,1]上单调递减,在区间[1,4),(4,+∞)上单调递增.即函数g(x)的单调递增区间为[1,4),(4,+∞),单调递减区间为(-∞,-2),(-2,1].规律方法　判断复合函数y=f(g(x))单调性的步骤:(1)确定函数的定义域;(2)找出复合函数的外层函数和内层函数,y=f(u),u=g(x);(3)分别确定这两个函数的单调性;(4)若这两个函数在对应的区间上单调性相同(同增或同减),则y=f(g(x))为增函数;若这两个函数在对应的区间上单调性相反(一增一减),则y=f(g(x))为减函数.此法则简记为“同增异减”.学以致用·随堂检测全达标12345671.(例1对点题)下列函数中,在区间(0,1)上单调递增的是(　　)A.y=|x+1| B.y=3-xC.y= D.y=-x2+4A 解析 由于x∈(0,1)时,y=|x+1|=x+1,所以该函数在(0,1)上单调递增,所以A选项正确;由于y=3-x是一次函数,在(0,1)上单调递减,所以B选项错误;由于y= 是反比例函数,在(0,1)上单调递减,所以C选项错误;由于y=-x2+4是二次函数,在(0,1)上单调递减,所以D选项错误.故选A.12345672.(例1变式题)若函数y=f(x)的图象如图所示,则函数f(x)的单调递增区间是　 . (-∞,1],(1,+∞)　 解析 由题图可知函数f(x)的单调递增区间是(-∞,1],(1,+∞). 1234567(1)求函数f(x)的定义域;(2)判断这个函数在(-∞,-2)上的单调性并用定义证明.123456712345674.(例3对点题)已知g(x)是定义在[-2,2]上的增函数,且g(t)>g(1-3t),求t的取值范围.12345675.(例4对点题)[2023陕西西安高一月考]如果函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上单调递减,那么实数a的取值范围是(　　)A.(-∞,-3] B.[-3,+∞)C.(-∞,5] D.[5,+∞)A 解析 ∵二次函数f(x)=x2+2(a-1)x+2的对称轴为直线x= =-(a-1)=1-a,抛物线开口向上,∴函数在(-∞,1-a]上单调递减,要使f(x)在区间(-∞,4]上单调递减,则1-a≥4,解得a≤-3.12345671234567C