人教A版高中数学必修第一册第5章三角函数5-5-1第2课时两角和与差的正弦、余弦、正切公式课件

这是一份人教A版高中数学必修第一册第5章三角函数5-5-1第2课时两角和与差的正弦、余弦、正切公式课件，共27页。

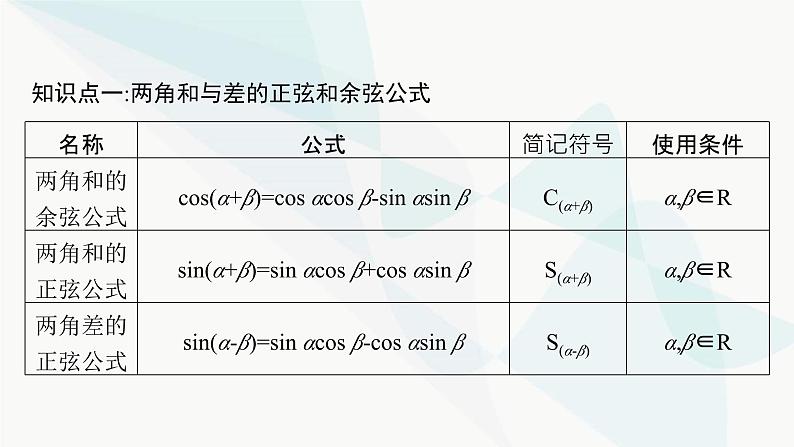
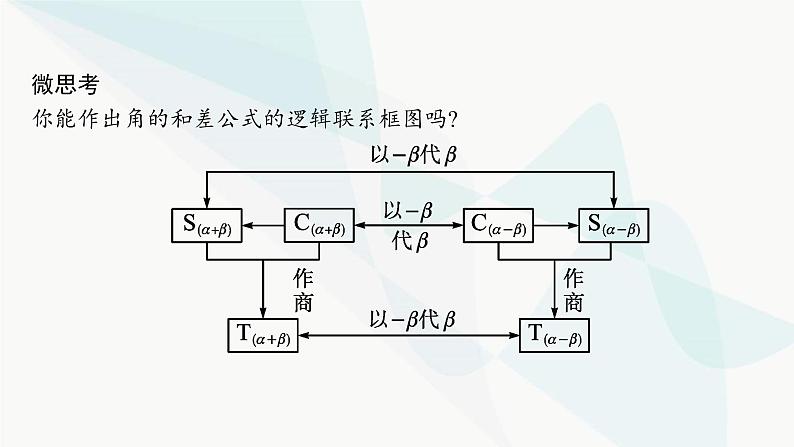
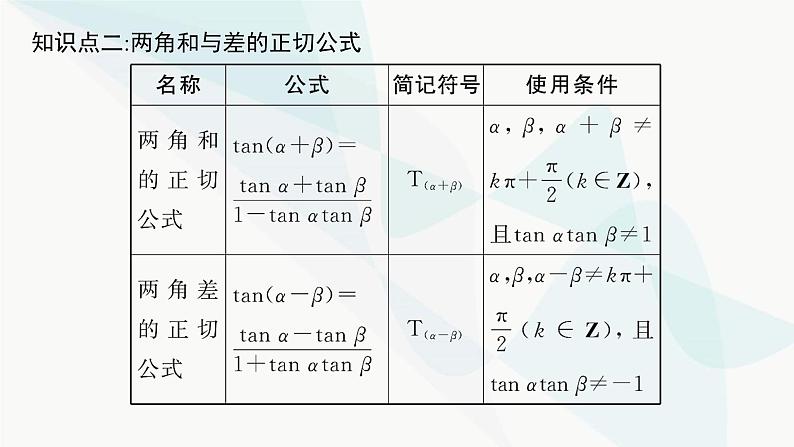
第五章5.5.1　第2课时　两角和与差的正弦、余弦、正切公式 基础落实·必备知识全过关重难探究·能力素养全提升目录索引 学以致用·随堂检测全达标基础落实·必备知识全过关知识点一:两角和与差的正弦和余弦公式 名师点睛两角和与差的正弦公式的记忆方法记忆口诀:正余余正,符号相同.“正余余正”表示展开后的两项分别是两角的正弦乘余弦、余弦乘正弦;“符号相同”表示展开后两项之间的连接符号与展开前两角之间的连接符号相同,即两角和时用“+”,两角差时用“-”.微思考你能作出角的和差公式的逻辑联系框图吗?知识点二:两角和与差的正切公式 名师点睛公式的右边为分式形式,其中分子为tan α,tan β的和或差.分母为1与tan αtan β的差或和.公式中左边的加减号与右边分子上的加减号相同,与分母上的加减号相反.符号变化规律可简记为“分子同,分母反”.当α,β,α±β角的正切值不存在时,不能使用上述公式,但可以用诱导公式或其他方法解题.重难探究·能力素养全提升问题1有了负数以后,和与差是可以相互转化的,如a+b=a-(-b).可否据此,由两角差的余弦公式推导两角和的余弦公式?问题2余弦与正弦可以通过余角相互转化,可否据此由两角和与差的余弦公式推导出两角和与差的正弦公式?问题3我们知道 ,如何利用这个公式,由两角和、差的正、余弦公式推导两角和、差的正切公式?探究点一 化简与求值问题4公式应用有时并不能直接套用,如何发现式子的结构特征、角与角之间的关系,以便利用公式化简?【例1】 化简下列各式:(2)cos(x+27°)cos(x-18°)+sin(x+27°)sin(x-18°);解 原式=cos[(x+27°)-(x-18°)]=cos 45°= . (3)tan 12°+tan 33°+tan 12°tan 33°;解 ∵ =tan(12°+33°)=tan 45°=1,∴tan 12°+tan 33°=1-tan 12°tan 33°,∴tan 12°+tan 33°+tan 12°tan 33°=1.(4)(1+tan 21°)(1+tan 22°)(1+tan 23°)·(1+tan 24°). 解 ∵(1+tan 21°)(1+tan 24°)=1+tan 21°+tan 24°+tan 21°tan 24°=1+tan(21°+24°)(1-tan 21°tan 24°)+tan 21°tan 24°=1+(1-tan 21°tan 24°)tan 45°+tan 21°tan 24°=1+1-tan 21°tan 24°+tan 21°tan 24°=2.同理可得(1+tan 22°)(1+tan 23°)=2,∴原式=2×2=4.规律方法　公式的巧妙运用①顺用:如本题中的(1);②逆用:如本题中的(2);③变用:变用涉及两个方面,一个是公式本身的变用,如cos(α+β)+sin αsin β=cos αcos β,一个是角的变用,也称为角的拆分变换,如α=(α+β)-β,2α=(α+β)+(α-β)等,从某种意义上来说,是一种整体思想的体现,如cos(α+β)cos β+sin(α+β)sin β=cos[(α+β)-β]=cos α.这些需要在平时的解题中多总结、多研究、多留心,唯其如此才能在解题中知道如何选择公式,选择哪一个公式会更好.探究点二 利用两角和与差的三角函数公式解决给值求值问题问题5对于给值求值问题,关键是如何用整体思想来理解已知角?如何构建已知角与所求角的关系?(1)求sin(α+β)的值;(2)求cos(α-β)的值;(3)求tan α的值.规律方法　给值求值的解题策略在解决此类题目时,一定要注意已知角与所求角之间的关系,恰当地运用拆角、凑角技巧,同时分析角之间的关系,利用角的代换化异角为同角,具体做法是:(1)当条件中有两角时,一般把“所求角”表示为已知两角的和或差.(2)当已知角有一个时,可利用诱导公式把所求角转化为已知角.探究点三 利用两角和与差的三角函数公式解决给值求角问题问题6对于给值求角问题,需要通过角对应的三角函数值来确定角,但一个三角函数值对应的角可能有多个,如何正确地确定角的范围?延伸探究 学以致用·随堂检测全达标123412342.(例2对点题)已知角α,β均为锐角,且cos α= ,tan(α-β)=- ,则tan β=　　　　　. 3 12343.(例2对点题)已知锐角α,β满足 ,求sin β的值.12344.(例3对点题)已知α,β均为锐角, ,求α-β.