





新高考数学一轮复习讲练测课件第1章§1.2常用逻辑用语 (含解析)
展开1.理解充分条件、必要条件、充要条件的意义;理解判定定理与充分条件、 性质定理与必要条件、数学定义与充要条件的关系.2.理解全称量词和存在量词的意义,能正确对两种命题进行否定.
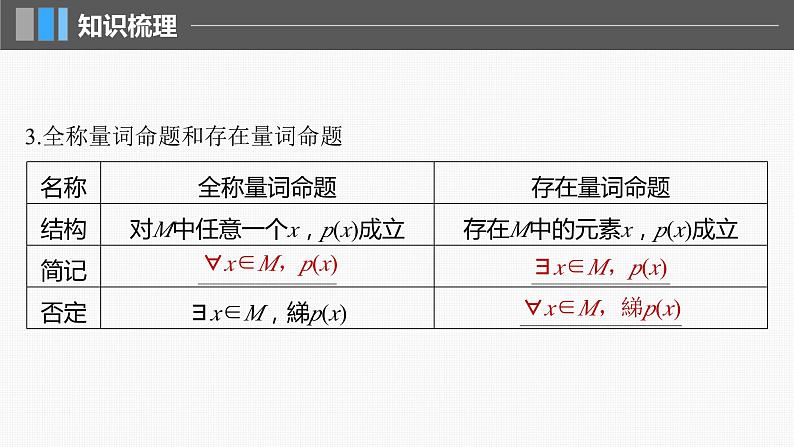
1.充分条件、必要条件与充要条件的概念
2.全称量词与存在量词(1)全称量词:短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“ ”表示.(2)存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“ ”表示.
3.全称量词命题和存在量词命题
1.充分、必要条件与对应集合之间的关系设A={x|p(x)},B={x|q(x)}.(1)若p是q的充分条件,则A⊆B;(2)若p是q的充分不必要条件,则AB;(3)若p是q的必要不充分条件,则BA;(4)若p是q的充要条件,则A=B.2.含有一个量词命题的否定规律是“改变量词,否定结论”.3.命题p与p的否定的真假性相反.
判断下列结论是否正确(请在括号中打“√”或“×”)(1)p是q的充分不必要条件等价于q是p的必要不充分条件.( )(2)“三角形的内角和为180°”是全称量词命题.( )(3)已知集合A,B,A∪B=A∩B的充要条件是A=B.( )
1.命题“∀x∈R,ex-1≥x”的否定是A.∃x∈R,ex-1≥x B.∀x∈R,ex-1≤xC.∃x∈R,ex-1
当x=0时,x2=0,所以A选项错误;当x∈R时,-1≤sin x≤1,所以B选项正确;因为2x>0,所以C选项错误;因为函数y=tan x∈R,所以D选项正确.
3.若“x>3”是“x>m”的必要不充分条件,则m的取值范围是__________.
因为“x>3”是“x>m”的必要不充分条件,所以(m,+∞)是(3,+∞)的真子集,由图可知m>3.
例1 (1)(2023·淮北模拟) “a>b>0”是“ >1”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件
(2)(2021·全国甲卷)等比数列{an}的公比为q,前n项和为Sn.设甲:q>0,乙:{Sn}是递增数列,则A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件
当a1<0,q>1时,an=a1qn-1<0,此时数列{Sn}单调递减,所以甲不是乙的充分条件.当数列{Sn}单调递增时,有Sn+1-Sn=an+1=a1qn>0,若a1>0,则qn>0(n∈N*),即q>0;若a1<0,则qn<0(n∈N*),不存在.所以甲是乙的必要条件.
充分条件、必要条件的两种判定方法(1)定义法:根据p⇒q,q⇒p进行判断,适用于定义、定理判断性问题.(2)集合法:根据p,q对应的集合之间的包含关系进行判断,多适用于条件中涉及参数范围的推断问题.
跟踪训练1 (1)(2022·长春模拟) “a·b=|a||b|”是“a与b共线”的A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
因为a·b=|a||b|cs〈a,b〉=|a||b|,所以cs〈a,b〉=1,因为〈a,b〉∈[0,π],所以〈a,b〉=0,所以a与b共线,当a与b共线时,〈a,b〉=0或〈a,b〉=π,所以a·b=|a||b|cs〈a,b〉=|a||b|或a·b=|a||b|cs〈a,b〉=-|a||b|,所以“a·b=|a||b|”是“a与b共线”的充分不必要条件.
(2)(多选)已知幂函数f(x)=(4m-1)xm,则下列选项中,能使得f(a)>f(b)成立的一个充分不必要条件是A. B.a2>b2C.ln a>ln b D.2a>2b
ln a>ln b⇔a>b>0,C符合题意;B,D选项中a,b均有可能为负数,B,D不符合题意.
例2 在①A∪B=B;②“x∈A”是“x∈B”的充分条件;③“x∈∁RA”是“x∈∁RB”的必要条件这三个条件中任选一个,补充到本题第(2)问的横线处,求解下列问题.问题:已知集合A={x|a≤x≤a+2},B={x|(x+1)(x-3)<0}.(1)当a=2时,求A∩B;(2)若________,求实数a的取值范围.注:如果选择多个条件分别解答,按第一个解答计分.
(1)由(x+1)(x-3)<0,解得-1
跟踪训练2 (2023·宜昌模拟)已知集合A={x|-2
由x2-2mx+m2-1<0,得[x-(m-1)][x-(m+1)]<0,所以m-1
命题点1 含量词命题的否定例3 (2022·漳州模拟)命题“∀a∈R,x2-ax+1=0有实数解”的否定是A.∀a∈R,x2-ax+1=0无实数解B.∃a∈R,x2-ax+1=0无实数解C.∀a∈R,x2-ax+1≠0有实数解D.∃a∈R,x2-ax+1≠0有实数解
因为全称量词命题的否定是存在量词命题,所以“∀a∈R,x2-ax+1=0有实数解”的否定是“∃a∈R,x2-ax+1=0无实数解”.
命题点2 含量词命题真假的判断例4 (多选)(2023·沈阳模拟)下列命题中为真命题的是A.∃x∈R, ≤1B.对于∀x∈R,n∈N*且n>1,都有 =xC.∀x∈R,ln(x-1)2≥0D.∃x∈R,ln x≥x-1
当x=1时,ln(x-1)2无意义,故C项是假命题;当x=1时,ln x≥x-1,故D项是真命题.
命题点3 含量词命题的应用
含量词命题的解题策略(1)判定全称量词命题是真命题,需证明都成立;要判定存在量词命题是真命题,只要找到一个成立即可.当一个命题的真假不易判定时,可以先判断其否定的真假.(2)由命题真假求参数的范围,一是直接由命题的真假求参数的范围;二是可利用等价命题求参数的范围.
跟踪训练3 (1)已知命题p:∃n∈N,n2≥2n+5,则綈p为A.∀n∈N,n2≥2n+5B.∃n∈N,n2≤2n+5C.∀n∈N,n2<2n+5D.∃n∈N,n2=2n+5
由存在量词命题的否定可知,綈p为∀n∈N,n2<2n+5.所以C正确,A,B,D错误.
(2)(多选)下列命题是真命题的是A.∀x∈R,-x2-1<0B.∀n∈Z,∃m∈Z,nm=mC.所有圆的圆心到其切线的距离都等于半径
∀x∈R,-x2≤0,所以-x2-1<0,故A项是真命题;当m=0时,nm=m恒成立,故B项是真命题;任何一个圆的圆心到切线的距离都等于半径,故C项是真命题;因为x2-2x+3=(x-1)2+2≥2,
(3)若命题“∃x∈R,x2+(a-1)x+1<0”的否定是假命题,则实数a的取值范围是_______________________.
命题“∃x∈R,x2+(a-1)x+1<0”的否定是假命题,则命题“∃x∈R,x2+(a-1)x+1<0”是真命题,即Δ=(a-1)2-4>0,解得a>3或a<-1,故实数a的取值范围是(-∞,-1)∪(3,+∞).
(-∞,-1)∪(3,+∞)
1.(2023·上饶模拟)“x2>2 021”是“x2>2 022”的A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
若x2>2 022,因为2 022>2 021,故x2>2 021,故“x2>2 022”可以推出“x2>2 021”,取x2=2 021.5,则满足x2>2 021,但x2>2 022不成立,所以“x2>2 021”不能推出“x2>2 022”,所以“x2>2 021”是“x2>2 022”的必要不充分条件.
2.已知命题p:∃x∈Q,使得x∉N,则綈p为A.∀x∉Q,都有x∉N B.∃x∉Q,使得x∈NC.∀x∈Q,都有x∈N D.∃x∈Q,使得x∈N
因为存在量词命题的否定是全称量词命题,所以由p:∃x∈Q,使得x∉N,得綈p:∀x∈Q,都有x∈N.
3.已知命题:“∀x∈R,方程x2+4x+a=0有解”是真命题,则实数a的取值范围是A.a<4 B.a≤4C.a>4 D.a≥4
“∀x∈R,方程x2+4x+a=0有解”是真命题,故Δ=16-4a≥0,解得a≤4.
4.(2023·武汉模拟)已知a,b是两条不重合的直线,α为一个平面,且a⊥α,则“b⊥α”是“a∥b”的A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
当b⊥α时,结合a⊥α,可得a∥b,充分性满足;当a∥b时,结合a⊥α,可得b⊥α,必要性满足.故“b⊥α”是“a∥b”的充要条件.
5.命题“∀1≤x≤2,x2-a≤0”为真命题的一个充分不必要条件是A.a≥4 B.a≥5C.a≤4 D.a≤5
因为命题“∀1≤x≤2,x2-a≤0”是真命题,所以∀1≤x≤2,a≥x2恒成立,所以a≥4,结合选项,命题是真命题的一个充分不必要条件是a≥5.
6.(多选)下列命题是真命题的是A.所有的素数都是奇数B.有一个实数x,使x2+2x+3=0C.“α=β”是“sin α=sin β”成立的充分不必要条件D.命题“∃x∈R,x+2≤0”的否定是“∀x∈R,x+2>0”
2是一个素数,但2是偶数,所以A是假命题;对于方程x2+2x+3=0,其中Δ=22-4×3=-8<0,所以不存在实数,使得x2+2x+3=0成立,所以B是假命题;由α=β⇒sin α=sin β,但由sin α=sin β不能得到α=β,故“α=β”是“sin α=sin β”成立的充分不必要条件,所以C是真命题;根据全称量词命题与存在量词命题的关系,可得命题“∃x∈R,x+2≤0”的否定是“∀x∈R,x+2>0”,所以D是真命题.
7.(多选)若“∃x∈(0,2),使得2x2-λx+1<0成立”是假命题,则实数λ可能的值是
由题意可知,命题“∀x∈(0,2),2x2-λx+1≥0成立”是真命题,
8.南北朝时期的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为V1,V2,被平行于这两个平面的任意平面截得的两个截面面积分别为S1,S2,则“S1,S2不总相等”是“V1,V2不相等”的A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
命题:如果“S1,S2不总相等”,那么“V1,V2不相等”的等价命题是:如果“V1,V2相等”,那么“S1,S2总相等”.
根据祖暅原理,当两个截面的面积S1,S2总相等时,这两个几何体的体积V1,V2相等,所以逆命题为真,故是必要条件;当两个三棱台,一正一反的放在两个平面之间时,此时体积相等,但截得截面面积未必相等,故是不充分条件,所以“S1,S2不总相等”是“V1,V2不相等”的必要不充分条件.
因为“sin x
x<-1(答案不唯一)
由于4x=22x,故2x>22x等价于x>2x,解得x<0,使得“2x>4x”成立的一个充分条件只需为集合{x|x<0}的子集即可.
11.已知命题“∃x∈{x|-2
若原命题为真命题,则∃x∈{x|-2
设A={x|x<2m-1或x>-m},B={x|x<2或x≥4},若α是β的必要条件,则B⊆A,
13.(多选)若“∀x∈M,|x|>x”为真命题,“∃x∈M,x>3”为假命题,则集合M可以是A.(-∞,-5) B.(-3,-1]C.(3,+∞) D.[0,3]
∵∃x∈M,x>3为假命题,∴∀x∈M,x≤3为真命题,可得M⊆(-∞,3],又∀x∈M,|x|>x为真命题,可得M⊆(-∞,0),∴M⊆(-∞,0).
14.一名法官在审理一起珍宝盗窃案时,四名嫌疑人甲、乙、丙、丁的供词如下:甲说:“罪犯在乙、丙、丁三人之中”;乙说:“我没有作案,是丙偷的”;丙说:“甲、乙两人中有一人是小偷”;丁说:“乙说的是事实”,经过调查核实,四人中有两人说的是真话,另外两人说的是假话,且这四人中只有一人是罪犯,由此可判断罪犯是______.
四人供词中,乙、丁意见一致,或同真或同假.若同真,即丙偷的,而四人有两人说的是真话,则甲、丙说的是假话,甲说“罪犯在乙、丙、丁三人之中”是假话,即乙、丙、丁没偷,相互矛盾;若同假,即不是丙偷的,则甲、丙说的是真话,甲说“罪犯在乙、丙、丁三人之中”,丙说“甲、乙两人中有一人是小偷”是真话, 可知罪犯是乙.
15.(2022·九江模拟)已知数列{an}满足a1=1,an+1=kan+k,则“数列{an}为等差数列”是“k=1”的A.充要条件 B.必要不充分条件C.充分不必要条件 D.既不充分也不必要条件
当k=1时,an+1=an+1,则{an}为等差数列,必要性成立;若{an}为等差数列,由a1=1,a2=2k,a3=2k2+k,
16.在△ABC中,角A,B,C所对的边分别为a,b,c,则“a>b”是“A+cs A>B+cs B”的A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件
2024年高考数学一轮复习讲练测(新教材新高考)第02讲 常用逻辑用语(课件): 这是一份2024年高考数学一轮复习讲练测(新教材新高考)第02讲 常用逻辑用语(课件),共24页。PPT课件主要包含了考情分析,网络构建,知识梳理题型归纳,真题感悟,PARTONE等内容,欢迎下载使用。
新高考数学一轮复习讲练测课件第8章§8.5椭圆 (含解析): 这是一份新高考数学一轮复习讲练测课件第8章§8.5椭圆 (含解析),共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,x轴和y轴,a2=b2+c2,命题点2待定系数法,命题点1离心率,因为点P在椭圆C上,即4c2=m2,又因为0e1等内容,欢迎下载使用。
新高考数学一轮复习讲练测课件第8章§8.3圆的方程 (含解析): 这是一份新高考数学一轮复习讲练测课件第8章§8.3圆的方程 (含解析),共60页。PPT课件主要包含了落实主干知识,探究核心题型,课时精练,=6y-12,-2-4等内容,欢迎下载使用。












