数学4.5 函数的应用（二）作业ppt课件

这是一份数学4.5 函数的应用（二）作业ppt课件，共18页。

1.已知函数f(x)的图象如图,其中零点的个数及可以用二分法求其零点的个数分别为(　　)A.4,4B.3,4C.5,4D.4,3
解析 由题图知函数f(x)与x轴有4个公共点,因此零点个数为4,从左往右数第4个公共点横坐标的左右两侧的函数值同号,因此不能用二分法求该零点,而其余3个均可使用二分法来求.故选D.
2.(多选题)下列函数中,有零点但不能用二分法求零点的近似值的是(　　)
解析 y= x2+4x+8= (x+4)2≥0,故不能用二分法求零点的近似值.y=|x|≥0,故不能用二分法求零点的近似值.易知选项A,B有零点,且可用二分法求零点的近似值.故选CD.
3.用二分法求函数f(x)=-x3-3x+5的近似零点时的初始区间是(　　)A.(1,3)B.(1,2)C.(-2,-1)D.(-3,-2)
解析 本题考查对用二分法求函数零点近似值的理解及初始区间的选择.∵f(1)=1,f(2)=-9,f(-1)=9,f(-2)=19,f(3)=-31,∴f(1)f(2)<0.又函数f(x)=-x3-3x+5的定义域为R,故f(x)的一个零点的近似值所在的初始区间为(1,2).
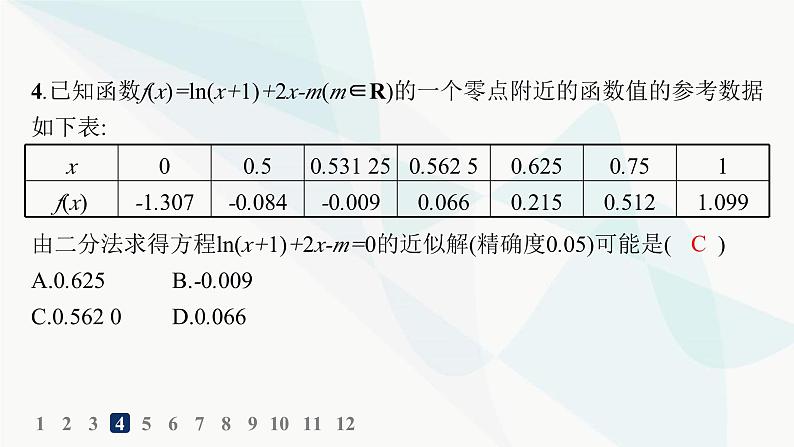
4.已知函数f(x)=ln(x+1)+2x-m(m∈R)的一个零点附近的函数值的参考数据如下表:
由二分法求得方程ln(x+1)+2x-m=0的近似解(精确度0.05)可能是(　　)B.-0.009 0
解析 设近似解为x0,因为f(0.531 25)<0,f(0.562 5)>0,所以x0∈(0.531 25,0.562 5).因为0.562 5-0.531 25=0.031 25<0.05,所以方程的近似解可取为0.562 0,故选C.
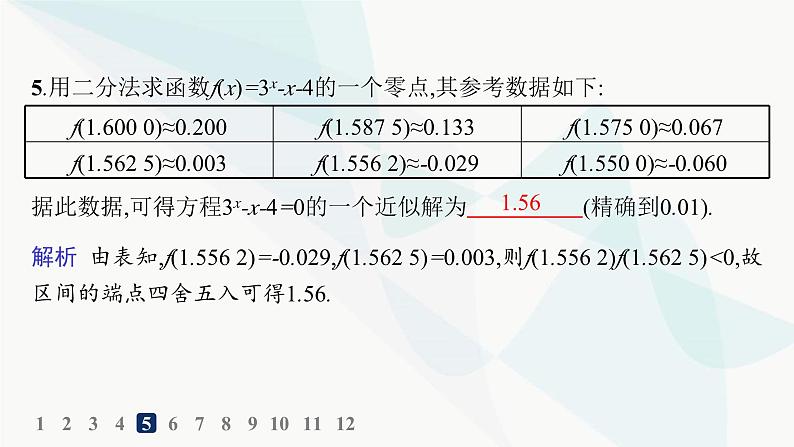
5.用二分法求函数f(x)=3x-x-4的一个零点,其参考数据如下:
据此数据,可得方程3x-x-4=0的一个近似解为　　　　　(精确到0.01). 
解析 由表知,f(1.556 2)=-0.029,f(1.562 5)=0.003,则f(1.556 2)f(1.562 5)<0,故区间的端点四舍五入可得1.56.
6.用二分法求函数f(x)=ln x-2+x在区间[1,2]上零点的近似值,先取区间中点c= ,则下一个含零点的区间是　　　　　. 
7.下表是连续函数f(x)在区间[1,2]上一些点的函数值:
由此可判断,方程f(x)=0的一个近似解.(精确到0.1)
解 由题中表格对应的数值可得,函数零点一定在区间[1.406 5,1.438]上,由精确度可知近似解可为1.4.
8.已知函数f(x)=ln x+2x-6.(1)证明:f(x)有且只有一个零点;(2)求这个零点所在的一个区间,使这个区间的长度不大于 .
∴f(x1)>f(x2),即f(x)=ln x+2x-6在(0,+∞)上是增函数,∴f(x)至多有一个零点.又f(2)=ln 2-2<0,f(3)=ln 3>0,∴f(2)·f(3)<0,即f(x)在(2,3)内有一个零点.∴f(x)在(0,+∞)上只有一个零点.
9.在用二分法求 的近似值的过程中,可以构造函数f(x)=x2-2(x>0),我们知道f(1)·f(2)<0,所以 ∈(1,2),要使 的近似值满足精确度为0.1,则对区间(1,2)至少二等分的次数为(　　)A.3B.4C.5D.6
解析 设要计算n次,则n满足 ,即2n>10.故计算4次就可满足要求.所以将区间(1,2)等分的次数为4次.故选B.
10.用二分法求方程ln x- =0在[1,2]上的根时,取中点c=1.5,则下一个有根区间为(　　)A.(1,1.25)B.(1,1.5)C.(1,2)D.(1.5,2)
解析 由二分法的步骤可知:①零点在区间(0,4)内,则有f(0)·f(4)<0,不妨设f(0)>0,f(4)<0,取中点2;②零点在区间(0,2)内,则有f(0)·f(2)<0,则f(0)>0,f(2)<0,取中点1;③零点在区间(1,2)内,则有f(1)·f(2)<0,
12.证明函数f(x)=x3-x2+5,x∈[-2,-1]有零点,并指出用二分法求零点的近似值(精确度0.1)时,至少需要进行多少次函数值的计算.
解 因为f(-2)=-8-4+5=-7<0,f(-1)=-1-1+5=3>0,所以f(-2)·f(-1)<0,所以函数f(x)=x3-x2+5在区间[-2,-1]上有零点x0.至少需要进行3次函数值的计算,理由如下: