山东省济南市历城区稼轩学校2022-2023学年七年级上学期月考数学试卷（10月份）+

这是一份山东省济南市历城区稼轩学校2022-2023学年七年级上学期月考数学试卷（10月份）+，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

山东省济南市历城区稼轩学校2022-2023学年七年级上学期月考数学试卷（10月份）（解析版）
一、选择题（本大题共10个小题，每题4分，共40分）
1．（4分）﹣的绝对值是（　　）
A．﹣ B．﹣2 C． D．2
2．（4分）如图所示几何体的左视图是（　　）

A． B． C． D．
3．（4分）2022年国内生产总值约991000亿元，则数字991000用科学记数法可表示为（　　）
A．991×103 B．99.1×104 C．9.91×105 D．9.91×108
4．（4分）下表是几种液体在标准大气压下的沸点，则沸点最高的液体是（　　）
液体名称
液态氧
液态氢
液态氮
液态氦
沸点/℃
﹣183
﹣253
﹣196
﹣268.9
A．液态氧 B．液态氢 C．液态氮 D．液态氦
5．（4分）下列计算正确的是（　　）
A．23＝2×3＝6 B．﹣32＝﹣3×（﹣3）＝9
C．（﹣2）3＝﹣8 D．
6．（4分）如图是由大小相同的小正方体组成的简单几何体的从左面看和从上面看，那么组成这个几何体的小正方体的个数最少为（　　）个．

A．3 B．4 C．5 D．6
7．（4分）设a是最小的自然数，b是最大的负整数，c是绝对值最小的有理数（　　）
A．﹣1 B．0 C．1 D．2
8．（4分）已知|a|＝6，|b|＝4，且a＜b（　　）
A．﹣2 B．﹣2或﹣10 C．﹣10 D．以上都不是
9．（4分）如图，把周长为3个单位长度的圆放到数轴（单位长度为1）上，A，B，C三点将圆三等分，然后将圆沿着数轴正方向滚动，依次为点B与数轴上表示2的点重合，点A与数轴上表示4的点重合，…，若当圆停止运动时点B正好落到数轴上（　　）

A．2020 B．2021 C．2022 D．2023
10．（4分）如图是有理数a、b在数轴上的位置，下列结论：①a+b＜0；②a2＞b2；③|a+b|＜|a|+|b|；④＞﹣1，其中正确的是（　　）

A．①② B．①②③ C．①②④ D．①②③④
二、填空题（本大题共6个小题，每题4分，共24分）
11．（4分）下列几何体：①圆柱；②正方体；③棱柱；在这些几何体中截面可能是圆的有 　 　．（只填写序号即可）
12．（4分）当流星划过夜空，空中会留下一条美丽的线，此现象用数学原理可解释为 　 　．
13．（4分）比较大小：﹣　 　﹣1（用“＞”或“＜”填空）．
14．（4分）数轴上与﹣1的距离等于3个单位长度的点所表示的数为 　 　．
15．（4分）若|a﹣2|+（b+3）2＝0，则ba＝　 　．
16．（4分）小颖同学到学校领来n盒粉笔，整齐地摞在讲桌上，从三面看到的平面图形如图所示　 　．

三、解答题（本题共7个小题，共57分）
17．（20分）计算题：
①（﹣3）﹣（﹣1.5）﹣（﹣3）+（+3.5）；
②；
；
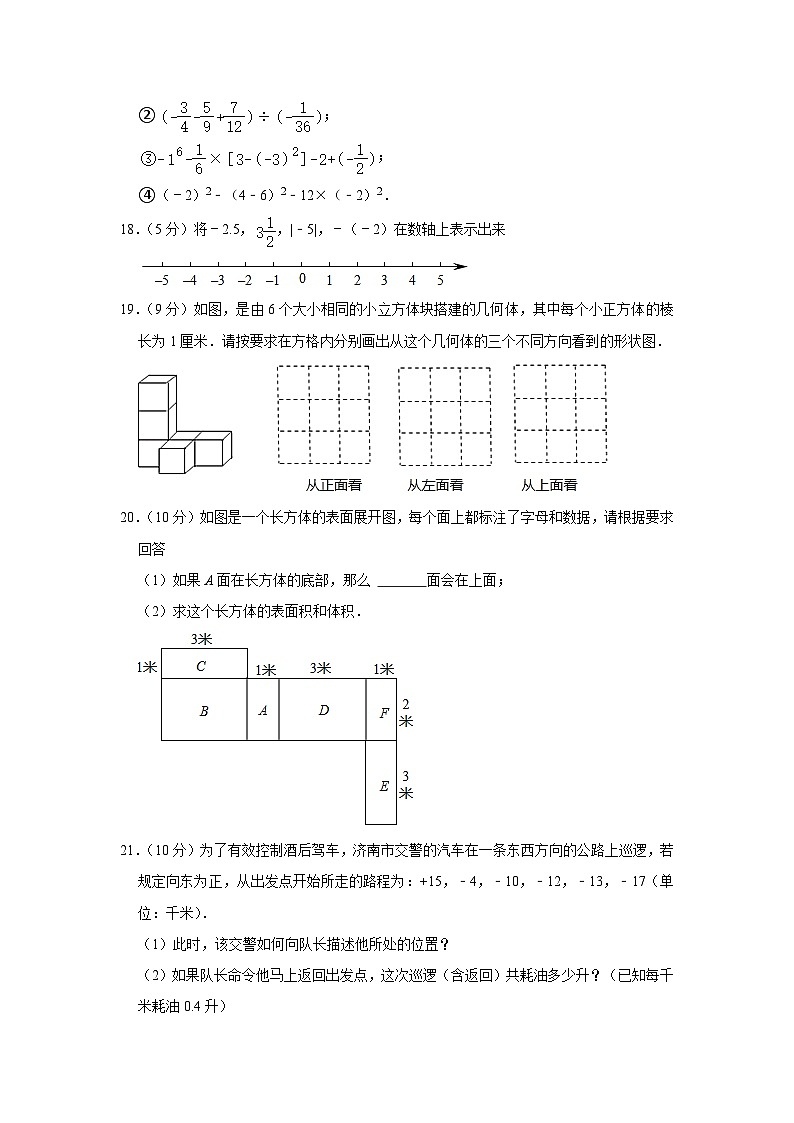
④（﹣2）2﹣（4﹣6）2﹣12×（﹣2）2．
18．（5分）将﹣2.5，，|﹣5|，﹣（﹣2）在数轴上表示出来

19．（9分）如图，是由6个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．

20．（10分）如图是一个长方体的表面展开图，每个面上都标注了字母和数据，请根据要求回答
（1）如果A面在长方体的底部，那么 　 　面会在上面；
（2）求这个长方体的表面积和体积．

21．（10分）为了有效控制酒后驾车，济南市交警的汽车在一条东西方向的公路上巡逻，若规定向东为正，从出发点开始所走的路程为：+15，﹣4，﹣10，﹣12，﹣13，﹣17（单位：千米）．
（1）此时，该交警如何向队长描述他所处的位置？
（2）如果队长命令他马上返回出发点，这次巡逻（含返回）共耗油多少升？（已知每千米耗油0.4升）
22．（12分）“十•一”黄金周期间，北京故宫游园人数大幅度增加，在7天假期中每天旅游的人数较之前一天的变化情况如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
日期
1日
2日
3日
4日
5日
6日
7日
人数变化单位：万人
+3.2
+0.6
+0.3
+0.7
﹣1.3
+0.2
﹣2.4
（1）若9月30日故宫的游园人数为2.1万人，请你计算这7天中每天的游园人数．
（2）“十•一”黄金周期间，北京故宫游园人数最多和最少分别是哪一天？游园人数为多少？
（3）故宫门票是60元一张，请计算出“十•一”黄金周期间，北京故宫的门票总收入（万元）．
23．（8分）阅读材料：求1+2+22+23+24+⋯+22017的值．
解：设S＝1+2+22+23+24+⋯+22012+22017将等式两边同时乘以2，
得：2S＝2+22+23+24+25+⋯+22012+22018，
将两式作差，得：2S﹣S＝22018﹣1，
即S＝22018﹣1，
即1+2+22+23+24+⋯+22017＝22018﹣1，
仿照此法计算：1+2+22+23+24+⋯+2100＝　 　．
运用上面的运算方法计算：
S＝1+3+32+33+34+⋯+32018．
24．（12分）（1）数轴上表示﹣1的点与表示2的两点之间的距离为 　 　；
（2）若|a﹣3|＝2，|b+2|＝1，且点A，b，则A、B两点间的最大距离是 　 　，最小距离是 　 　；
（3）数轴上的A，B，C三点所表示的数分别为a，b，c．点A在点C左侧，点B与点C之间的距离为5，如果P，点P以每分钟2个单位长度的速度从点A向右运动，点Q以每分钟4个单位长度从点C向左运动．
①如图1，多少分钟后，点P与点B的距离和点Q与点B的距离相等；
②如图2，多少分钟后，点P与点B的距离和点Q与点B的距离相等．


参考答案与试题解析
一、选择题（本大题共10个小题，每题4分，共40分）
1．（4分）﹣的绝对值是（　　）
A．﹣ B．﹣2 C． D．2
【分析】根据绝对值的定义直接计算即可解答．
【解答】解：﹣的绝对值为．
故选：C．
【点评】本题主要考查绝对值的性质．绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．
2．（4分）如图所示几何体的左视图是（　　）

A． B． C． D．
【分析】根据左视图就是从物体的左边进行观察，得出左视图有1列，小正方形数目为2．
【解答】解：如图所示：
．
故选：A．
【点评】此题主要考查了三视图的画法中左视图画法，主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．
3．（4分）2022年国内生产总值约991000亿元，则数字991000用科学记数法可表示为（　　）
A．991×103 B．99.1×104 C．9.91×105 D．9.91×108
【分析】科学记数法的表现形式为a×10n的形式，其中1≤|a|＜10，n为整数，确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，当原数绝对值大于等于10时，n是正整数，当原数绝对值小于1时，n是负整数；由此进行求解即可得到答案．
【解答】解：991000＝9.91×105．
故选：C．
【点评】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．
4．（4分）下表是几种液体在标准大气压下的沸点，则沸点最高的液体是（　　）
液体名称
液态氧
液态氢
液态氮
液态氦
沸点/℃
﹣183
﹣253
﹣196
﹣268.9
A．液态氧 B．液态氢 C．液态氮 D．液态氦
【分析】根据有理数大小的比较方法解答即可．
【解答】解：∵|﹣268.9|＞|﹣253|＞|﹣196|＞|﹣183|，
∴﹣268.9＜﹣253＜﹣196＜﹣183，
∴沸点最高的液体是液态氧．
故选：A．
【点评】本题考查了有理数大小的比较．解题的关键是明确两个负数比较大小，绝对值大的反而小．
5．（4分）下列计算正确的是（　　）
A．23＝2×3＝6 B．﹣32＝﹣3×（﹣3）＝9
C．（﹣2）3＝﹣8 D．
【分析】根据有理数乘方的定义及运算法则，先计算出各选项的值，再比较即可．
【解答】解：A、23＝7×2×2＝6，故错误；
B、﹣32＝﹣（6×3）＝﹣9，故错误；
C、（﹣8）3＝（﹣2）×（﹣6）×（﹣2）＝﹣8，正确；
D、＝（﹣）＝．
故选：C．
【点评】本题考查了乘方的简单计算，并考查了负数的奇次幂为负数，负数的偶次幂为正数．
6．（4分）如图是由大小相同的小正方体组成的简单几何体的从左面看和从上面看，那么组成这个几何体的小正方体的个数最少为（　　）个．

A．3 B．4 C．5 D．6
【分析】根据简单组合体三视图的定义，在俯视图的相应位置标注需要正方体个数最少时的情况即可》
【解答】解：在俯视图的相应位置标注需要正方体个数最少时的情况如下：

所以最少需要小正方体的个数为1+1+2+1＝5（个），
故选：C．
【点评】本题考查简单组合体的三视图，理解视图的定义，掌握简单组合体三视图的画法及形状是正确解答的前提，在俯视图的相应位置标注需要正方体个数最少时的情况是解决问题的关键．
7．（4分）设a是最小的自然数，b是最大的负整数，c是绝对值最小的有理数（　　）
A．﹣1 B．0 C．1 D．2
【分析】最小的自然数为0，最大的负整数为﹣1，绝对值最小的有理数为0，由此可得出答案．
【解答】解：由题意得：a＝0，b＝﹣1，
∴a﹣b+c＝7．
故选：C．
【点评】本题考查有理数的知识，难度不大，根据题意确定a、b、c的值是关键．
8．（4分）已知|a|＝6，|b|＝4，且a＜b（　　）
A．﹣2 B．﹣2或﹣10 C．﹣10 D．以上都不是
【分析】利用绝对值的代数意义求出a与b的值，即可确定出a+b的值．
【解答】解：∵|a|＝6，|b|＝4，
∴a＝﹣5，b＝4，b＝﹣4，
则a+b＝﹣7或﹣10，
故选：B．
【点评】此题考查了有理数的加法，以及绝对值，熟练掌握运算法则是解本题的关键．
9．（4分）如图，把周长为3个单位长度的圆放到数轴（单位长度为1）上，A，B，C三点将圆三等分，然后将圆沿着数轴正方向滚动，依次为点B与数轴上表示2的点重合，点A与数轴上表示4的点重合，…，若当圆停止运动时点B正好落到数轴上（　　）

A．2020 B．2021 C．2022 D．2023
【分析】根据圆的滚动规律可知3次一个循环，将各选项中的数字除以3，根据余数可判定求解．
【解答】解：由题意得：圆沿着数轴正方向滚动一次按A，B，C的顺序 排列：
A.2020÷3＝673…1，所以此时点A正好落在数轴上；
B.2021÷5＝673…2，所以此时点B正好落在数轴上；
C.2022÷3＝674，所以此时点C正好落在数轴上；
D.2023÷4＝674…1，所以此时点A正好落在数轴上．
故选：B．
【点评】本题主要考查数轴，找规律，找到圆的滚动规律是解题的关键．
10．（4分）如图是有理数a、b在数轴上的位置，下列结论：①a+b＜0；②a2＞b2；③|a+b|＜|a|+|b|；④＞﹣1，其中正确的是（　　）

A．①② B．①②③ C．①②④ D．①②③④
【分析】根据数轴上点的位置关系，可得a、b的大小范围，再分别根据有理数的加法法则，有理数的乘方的定义，绝对值的性质以及有理数的除法法则判断即可．
【解答】解：由数轴上点的位置，得a＜0＜b，
①a+b＜0，正确；
②a6＞b2，正确；
③|a+b|＜|a|+|b|，正确；
④＜﹣1．
所以正确的是①②③．
故选：B．
【点评】本题考查了有理数大小比较，利用了数轴上的点表示的数右边的总比左边的大，负数的奇数次幂是负数．
二、填空题（本大题共6个小题，每题4分，共24分）
11．（4分）下列几何体：①圆柱；②正方体；③棱柱；在这些几何体中截面可能是圆的有 　①④　．（只填写序号即可）
【分析】根据每一个几何体的截面图形判断即可．
【解答】解：因为：正方体，棱柱的截面只可能是多边形，圆柱，
所以上列几何体：①圆柱；②正方体；④球，
故答案为：①④．
【点评】本题考查了截一个几何体，熟练掌握每一个几何体的截面图形是解题的关键．
12．（4分）当流星划过夜空，空中会留下一条美丽的线，此现象用数学原理可解释为 　点动成线　．
【分析】流星是点，光线是线，所以说明点动成线．
【解答】解：“当流星划过夜空，空中会留下一条美丽的线．
故答案为：点动成线．
【点评】此题主要考查了点、线、面、体，关键是掌握点动成线，线动成面，面动成体．
13．（4分）比较大小：﹣　＜　﹣1（用“＞”或“＜”填空）．
【分析】两个负数比较大小，绝对值大的其值反而小，据此判断即可．
【解答】解：∵||＞|﹣8|，
∴．
故答案为：＜．
【点评】本题考查了有理数大小比较，要熟练掌握并正确运用有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数比较大小，绝对值大的其值反而小．
14．（4分）数轴上与﹣1的距离等于3个单位长度的点所表示的数为 　﹣4或2　．
【分析】根据数轴上与一点距离相等的点有两个，可得答案．
【解答】解：数轴上与﹣1的距离等于3个单位长度的点所表示的数为﹣8或2．
故答案为：﹣4或8．
【点评】本题考查了数轴，数轴上于一点距离相等的点有两个，以防漏掉．
15．（4分）若|a﹣2|+（b+3）2＝0，则ba＝　9　．
【分析】根据绝对值和偶次方的非负性求出a、b的值即可得到答案．
【解答】解：∵|a﹣2|+（b+3）6＝0，|a﹣2|≥72≥0，
∴a﹣5＝0，b+3＝2，
∴a＝2，b＝﹣3，
∴ba＝（﹣4）2＝9，
故答案为：5．
【点评】本题主要考查了非负数的性质，代数式求值，熟知非负数的性质是解题的关键．
16．（4分）小颖同学到学校领来n盒粉笔，整齐地摞在讲桌上，从三面看到的平面图形如图所示　7　．

【分析】首先根据俯视图判断最底层的个数，然后结合主视图和左视图判断出该总盒数．
【解答】解：由俯视图可得最底层有4盒，由正视图和左视图可得第二层有2盒，共有7盒，
故答案为：7．
【点评】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．
三、解答题（本题共7个小题，共57分）
17．（20分）计算题：
①（﹣3）﹣（﹣1.5）﹣（﹣3）+（+3.5）；
②；
；
④（﹣2）2﹣（4﹣6）2﹣12×（﹣2）2．
【分析】①原式利用减法法则变形，计算即可求出值；
②原式利用除法法则变形，再利用乘法分配律计算即可求出值；
③原式先算括号中的运算，再算乘方，然后算乘除，最后算加减即可求出值；
④原式先算乘方，再算乘除，最后算加减即可求出值．
【解答】解：①原式＝﹣3+1.3+3+3.7
＝（﹣3+3）+（5.5+3.4）
＝0+5
＝2；
②原式＝（﹣﹣+）×（﹣36）
＝×36+×36
＝27+20﹣21
＝26；
③原式＝﹣16﹣×（2﹣9）﹣2+（﹣）
＝﹣1﹣×（﹣6）﹣6+（﹣）
＝﹣7+1﹣2+（﹣）
＝﹣2；
④原式＝4﹣3﹣12×4
＝0﹣48
＝﹣48．
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
18．（5分）将﹣2.5，，|﹣5|，﹣（﹣2）在数轴上表示出来

【分析】首先把每个数表示在数轴上，再根据数轴比较大小即可．
【解答】解：如图，

用“＞”连接为：|﹣5|＞3＞﹣（﹣2）＞﹣5.5．
【点评】本题考查实数的大小比较，能把每个数准确地表示在数轴上是解题关键．
19．（9分）如图，是由6个大小相同的小立方体块搭建的几何体，其中每个小正方体的棱长为1厘米．请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．

【分析】根据三视图的定义作出图形即可．
【解答】解：三视图如图所示：

【点评】本题考查作图﹣三视图，解题的关键是理解三视图的定义，则有中考常考题型．
20．（10分）如图是一个长方体的表面展开图，每个面上都标注了字母和数据，请根据要求回答
（1）如果A面在长方体的底部，那么 　F　面会在上面；
（2）求这个长方体的表面积和体积．

【分析】（1）根据展开图，可得几何体，A、B、C是邻面，D、F、E是邻面，根据A面在底面，F会在上面，可得答案；
（2）由矩形的表面积和体积计算公式解答．
【解答】解：（1）如图所示，A与F是对面，那么 F面会在上面；
故答案为：F；

（2）这个长方体的表面积是：2×（1×4+1×2+2×3）＝22（米2）．
这个长方体的体积是：6×2×3＝8（米3）．

【点评】本题考查了几何体的展开图，利用了几何体展开图组成几何体时面与面之间的关系．
21．（10分）为了有效控制酒后驾车，济南市交警的汽车在一条东西方向的公路上巡逻，若规定向东为正，从出发点开始所走的路程为：+15，﹣4，﹣10，﹣12，﹣13，﹣17（单位：千米）．
（1）此时，该交警如何向队长描述他所处的位置？
（2）如果队长命令他马上返回出发点，这次巡逻（含返回）共耗油多少升？（已知每千米耗油0.4升）
【分析】（1）根据有理数的加法运算以及正数、负数的符号表示的实际意义解决此题．
（2）先确定行驶的路程，再计算耗油量．
【解答】解：（1）+15+（﹣4）+13+（﹣10）+（﹣12）+3+（﹣13）+（﹣17）
＝﹣25（千米）．
∴该交警在公路西侧25千米处．
（2）交警共行驶的路程为|+15|+|﹣7|+|+13|+|﹣10|+|﹣12|+|+3|+|﹣13|+|﹣17|+|﹣25|＝112（千米）．
∴这次巡逻（含返回）共耗油112×0.7＝44.8（升）．
答：这次巡逻（含返回）共耗油44.8升．
【点评】本题主要考查有理数的加法运算以及正数、负数的符号表示的实际意义，熟练掌握有理数的加法运算法则以及正数、负数的符号表示的实际意义是解决本题的关键．
22．（12分）“十•一”黄金周期间，北京故宫游园人数大幅度增加，在7天假期中每天旅游的人数较之前一天的变化情况如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）：
日期
1日
2日
3日
4日
5日
6日
7日
人数变化单位：万人
+3.2
+0.6
+0.3
+0.7
﹣1.3
+0.2
﹣2.4
（1）若9月30日故宫的游园人数为2.1万人，请你计算这7天中每天的游园人数．
（2）“十•一”黄金周期间，北京故宫游园人数最多和最少分别是哪一天？游园人数为多少？
（3）故宫门票是60元一张，请计算出“十•一”黄金周期间，北京故宫的门票总收入（万元）．
【分析】（1）根据每一天的人数比前一天的变化情况，求出各天的游客人数，
（2）根据（1）的结果进行判断即可，
（3）求出这7天的总游客人数，即可求出门票总收入，
【解答】解：（1）10月1日  5.4万人 5.9万人 8.2万人 6.7万人 5.6万人，10月8日 ；
（2）游园人数最多的是10月4日，达到6.7万人，3.4万人；
（3）60×（4.3+5.4+6.2+4.9+5.3+5.8+8.4）＝2346万元，
答：北京故宫的门票总收入2346万元．
【点评】本题考查正数、负数的意义，折线统计图的意义和制作方法，从统计表中获取数量及数量关系式解决问题的关键．
23．（8分）阅读材料：求1+2+22+23+24+⋯+22017的值．
解：设S＝1+2+22+23+24+⋯+22012+22017将等式两边同时乘以2，
得：2S＝2+22+23+24+25+⋯+22012+22018，
将两式作差，得：2S﹣S＝22018﹣1，
即S＝22018﹣1，
即1+2+22+23+24+⋯+22017＝22018﹣1，
仿照此法计算：1+2+22+23+24+⋯+2100＝　2101﹣1　．
运用上面的运算方法计算：
S＝1+3+32+33+34+⋯+32018．
【分析】设S＝1+2+22+23+24+…+2100，将等式两边同时乘以2得到另一等式，两式相减即可得到1+2+22+23+…+2100的值；
设S＝1+3+32+33+34+…+32018，两边同时乘以3得另一等式，两式相减即可得到2倍的1+3+32+33+34+…+32018的值，进而得出答案．
【解答】解：设S＝1+2+72+26+24+…+5100，
将等式两边同时乘以2得：2S＝7+22+73+25+…+2100+2101，
将下式减去上式得：5S﹣S＝2101﹣1，即S＝5101﹣1，
则1+6+22+33+24+…+2100＝2101﹣8；
设S＝1+3+52+33+34+…+62018①，
两边同时乘以3得：3S＝2+32+83+33+…+32019②，
②﹣①得：3S﹣S＝32019﹣1，即S＝
即1+8+32+23+35+…+32018＝．
故答案为：2101﹣4．
【点评】本题考查有理数的乘方，解题的关键是明确题意，运用题目中的解题方法，运用类比的数学思想解答问题．
24．（12分）（1）数轴上表示﹣1的点与表示2的两点之间的距离为 　3　；
（2）若|a﹣3|＝2，|b+2|＝1，且点A，b，则A、B两点间的最大距离是 　8　，最小距离是 　2　；
（3）数轴上的A，B，C三点所表示的数分别为a，b，c．点A在点C左侧，点B与点C之间的距离为5，如果P，点P以每分钟2个单位长度的速度从点A向右运动，点Q以每分钟4个单位长度从点C向左运动．
①如图1，多少分钟后，点P与点B的距离和点Q与点B的距离相等；
②如图2，多少分钟后，点P与点B的距离和点Q与点B的距离相等．

【分析】（1）根据两点间的距离公式即可求解；
（2）根据绝对值的性质求得a，b，进一步得到A、B两点间的最大距离和最小距离即可求解；
（3）①设x分钟后，点P与点B的距离和点Q与点B的距离相等，根据等量关系列出方程求解即可；
②设y分钟后，点P与点B的距离和点Q与点B的距离相等，根据等量关系列出方程求解即可．
【解答】解：（1）数轴上表示﹣1的点与表示2的两点之间的距离为6﹣（﹣1）＝3．
故答案为：4；
（2）∵|a﹣3|＝2，|b+6|＝1，
∴a﹣3＝±5，b+2＝±1，
解得a＝2或5，b＝﹣3或﹣3，
故A、B两点间的最大距离是5﹣（﹣3）＝7．
故答案为：8，2；
（3）①如图8，设x分钟后，依题意有，
3﹣2x＝8﹣4x，
解得x＝1；
或6x+4x＝3+6，
解得x＝．
故2或分钟后；
②如图5，设y分钟后，依题意有，
2y+4y＝6﹣3，
解得y＝；
或3+2y＝8y﹣5，
解得y＝4．
故或4分钟后．
【点评】本题考查了一元一次方程的应用，数轴，根据题目给出的条件，找出合适的等量关系列出方程，再求解；（3）分类讨论是解题的关键．