




还剩44页未读,
继续阅读
湘教版九上数学第2章一元二次方程章末复习课件
展开
这是一份湘教版九上数学第2章一元二次方程章末复习课件,共52页。
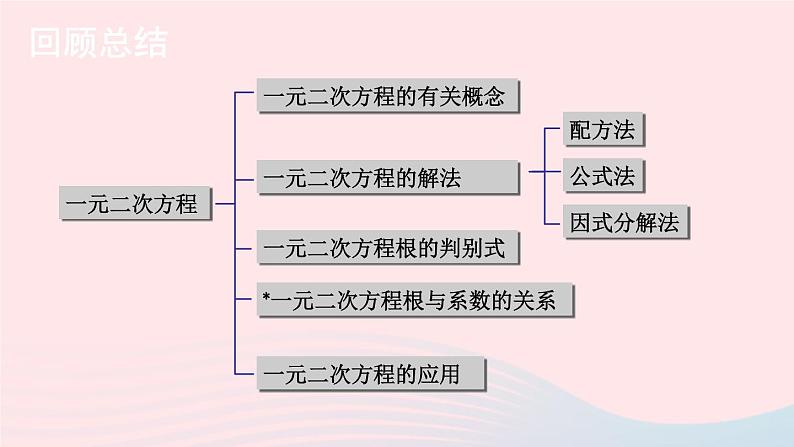
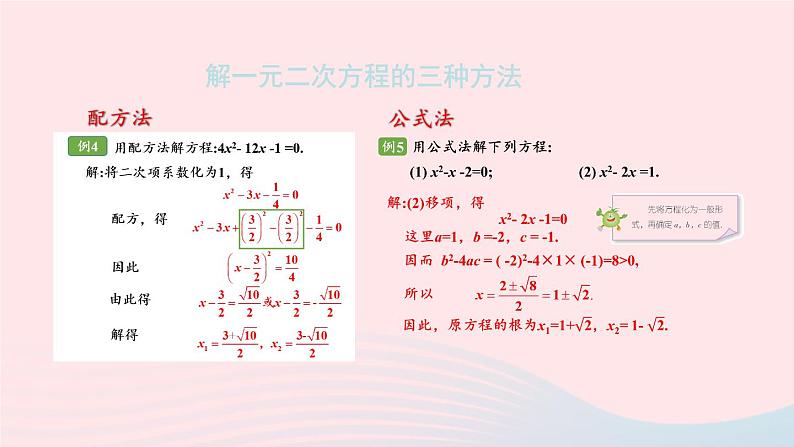
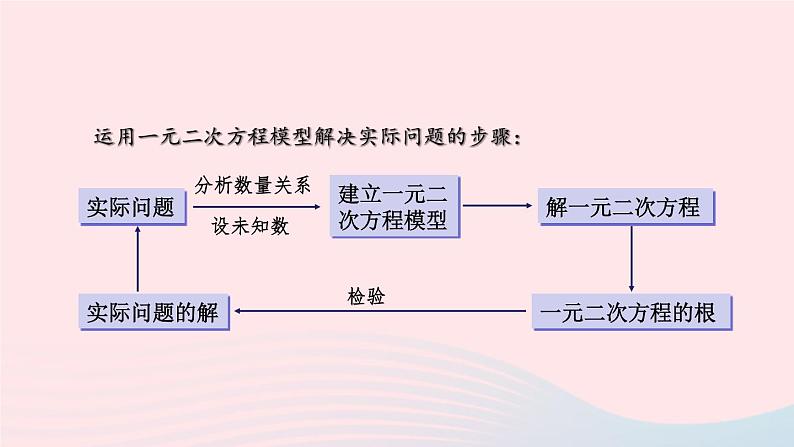
湘教·九年级上册章末复习回顾总结一元二次方程一元二次方程的有关概念一元二次方程的应用一元二次方程的解法一元二次方程根的判别式*一元二次方程根与系数的关系配方法公式法因式分解法如果一个方程通过整理可以使右边为0,而左边是只含有一个未知数的二次多项式,那么这样的方程叫作一元二次方程,它的一般形式是ax2+bx +c=0 (a,b,c是已知数,a≠0)对于一元二次方程ax2+bx +c=0 (a,b,c是已知数,a≠0) ,其中a, b,c分别叫作二次项系数、一次项系数、常数项.配方法解一元二次方程的三种方法公式法因式分解法一元二次方程ax2+ bx +c =0 (a≠0)的根的情况可由Δ = b2- 4ac来判断:当Δ >0时,原方程有两个不相等的实数根,其根为当Δ =0时,原方程有两个相等的实数根,其根为当Δ <0时,原方程没有实数根.即当Δ≥0时,一元二次方程的根与系数之间具有如下关系:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.韦达定理运用一元二次方程模型解决实际问题的步骤:实际问题建立一元二次方程模型解一元二次方程一元二次方程的根实际问题的解分析数量关系设未知数检验课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(1)原方程可化为5x2- 49=0所以该方程的二次项系数是5、一次项系数是0、常数项是-49.课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(2)原方程可化为x2+3x +5=0所以该方程的二次项系数是1、一次项系数是3、常数项是5.课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(3)原方程可化为0.01t2- 5t+ 1=0所以该方程的二次项系数是0.01、一次项系数是-5、常数项是1.课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(4)原方程可化为4y2+2y-9=0所以该方程的二次项系数是4、一次项系数是2、常数项是-9.2.解下列方程:(1) 49x2 - 144=0; (2) ( 1-x)2=1;(3)x2+8x +16=0; (4) x (7-x )=4x2;(5) x(x-2)-3x2=0; (6)x2-4x+4=64.解:原方程可化为根据平方根的意义,得因此,原方程的根为(1) 49x2 - 144=0; 解:根据平方根的意义,得因此,原方程的根为(2)(1-x)2=1解:原方程可化为根据平方根的意义,得因此,原方程的根为(3)x2+8x +16=0;解:原方程可化为5x2-7x =0.把方程左边因式分解,得x (5x -7)=0,由此得 x=0或 5x -7=0.解得 x1=0 ,x2 = .(4) x (7-x )=4x2解:原方程可化为x2+x =0.把方程左边因式分解,得x (x +1)=0,由此得 x=0或 x +1 =0.解得 x1=0 ,x2 =-1.(5) x(x-2)-3x2=0(6)x2-4x+4=64解:原方程可化为(x-2)2=64.根据平方根的意义,得因此,原方程的根为3.解下列方程:(1)2x2-6x- 3=0; (2) x (x +5)= 24;(3) x (x +1)+2 (x-1) =0; (4) (x-3)2+2x ( x -3 )=0;(5) 3(x-2)2=x (x-2).解:这里a=2,b =-6,c = -3.因而 b2-4ac = ( -6)2-4×2× (-3)=36+24=60>0,因此,原方程的根为 .所以(1)2x2-6x- 3=0(2) x (x +5)= 24解:原方程可化为x2+5x -24=0.把方程左边因式分解,得(x-3) (x +8)=0,由此得 x-3=0或 x +8 =0.解得 x1=3 ,x2 =-8.(3) x (x +1)+2 (x-1) =0解:原方程可化为因而 b2-4ac = 32-4×1× (-2)=9+8=17>0,因此,原方程的根为 .所以这里a=1,b =3,c = -2.x2+3x -2=0.(4) (x-3)2+2x ( x -3 )=0解:把方程左边因式分解,得(x-3) (x -3+2x)=0,由此得 x-3=0或 3x -3 =0,解得 x1=3 ,x2 =1.即 (x-3) (3x -3)=0(5) 3(x-2)2=x (x-2)解:原方程可化为3(x-2)2-x (x-2)=0把方程左边因式分解,得(x-2) [3(x -2)-x]=0,由此得 x-2=0或 2x -6 =0.解得 x1=2 ,x2 =3.即 (x-2) (2x -6)=04.不解方程,利用判别式判断下列方程的根的情况.(1) 4x2+6x+9=0; (2) y2=y+5.解:(1)因为Δ = b2-4ac =62-4×4×9 =36+ 144 =-108<0,所以,原方程没有实数根.解:(2)将原方程化为一般形式,得y2-y-5=0因为Δ =b2-4ac = ( -1 )2-4×1×(-5) =1+20=21>0,所以,原方程有两个不相等的实数根.(2) y2=y+5*5.设x1,x2,是方程2x2-6x+3=0的两根,求下列各式的值:(1) x1+x2; (2)x1x2; (3) x12+x22.解:*6.若方程x2-3x -1=0的两根为x1,x2,求 的值.解:由韦达定理得7.已知三个连续奇数的平方和是371,求这三个奇数.解:设三个连续奇数中间的奇数为x.由题意得(x-2)2+x2+(x+2)2=371整理,得x2=121解得 x1=11 ,x2 =-11.所以这三个奇数为9,11,13或-13,-11,-9.8.北京奥运会的主会场“鸟巢”给世人留下了深刻的记忆.据了解,在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结构用钢量从最初的54000 t减少到42000 t.求平均每次用钢量降低的百分率x(精确到1%).解:根据等量关系得54000( 1-x)2=42000.整理,得 ( 1-x )2= .解得 (不合题意,舍去).答:平均每次用钢量降低的百分率为12%.9.将一块长方形桌布铺在长为1.5 m、宽为1 m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍.求桌布下垂的长度.解:设桌布下垂的长度为x m,则根据等量关系得(2x+1.5)(2x+1)=1.5×1×2整理,得 8x2+10x-3=0,解得 x1=0.25 ,x2 =-1.5(不合题意,舍去).答:桌布下垂的长度为0.25m,10.如图为一张方格纸,纸上有一三角形(上色部分),其顶点均位于网格线的交点上.若上色部分的三角形面积为15.75 cm2,则此方格纸的面积为多少?解:设每个小方格的边长为x cm.根据题意得整理,得 x2=2.25解得 x1=1.5 ,x2 =-1.5(不合题意,舍去).所以此方格纸的面积为4×1.5×4×1.5=36cm2.11.现有一块矩形钢板ABCD,长AD=7.5 m,宽AB=5 m.在这块钢板上截除两个正方形得到如图所示的模具(阴影部分所示).已知 BE= DF,且模具的面积等于原矩形钢板的面积的一半,求DF的长(精确到0.1 m).7.5 m5 mx mx m解:设DF长为x m.∵DF+FC=DC=AB=5m,∴PC=FC=(5-x)m.∵BE+EP+PC=BC=AD=7.5m,∴EP=2.5m.依题意得即 2x2-20x+25=0.解得,由于x2>5,因而舍去.答:DF长约为1.5m.12.如图,在 Rt △ABC中,∠B= 90°,AC= 10 cm,BC=6 cm.现有两点P,Q分别从点A 和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2 cm/s,1 cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.问是否存在这样的x,使得四边形APQC的面积等于16 cm2?若存在,请求出此时x的值;若不存在,请说明理由.解:根据题意,得AP=2x cm,CQ=x cm,假设存在这样的x,使得四边形APQC的面积等于16 cm2.∵∠B=90°,AC=10,BC=6, ∴AB=8,BQ=(6-x)cm,BP=(8-2x)cm.整理,得 x2-10x+16=0解得 x1=2 ,x2 =8.但x2 =8时不合题意,因为P从A到B只需4s.所以当x=2时,正好四边形APQC的面积等于16cm2.B 组13.解下列方程:(1)( 3x+5 )2-6 ( 3x+5 )+9=0; (2) x2+ax - 2a2=0(a为常数).解:把方程左边因式分解,得[ (3x +5)-3]2=0,由此得 (3x +5)-3=0,解得 x1=x2 = .(1)( 3x+5 )2-6 ( 3x+5 )+9=0; 解:把方程左边因式分解,得(x -a)(x+2a)=0,由此得 x-a=0或 x +2a =0,解得 x1=a,x2 = -2a.(2) x2+ax - 2a2=0(a为常数).14.已知 a,b,c分别是△ABC的三边,其中a=1,c=4,且关于x的方程x2-4x +b=0有两个相等的实数根,试判断△ABC的形状.解:依题意得关于x的方程x2-4x +b=0的判别式Δ=b2-4ac=(-4)2-4×1×b=0即 16-4b=0∴b=4=c≠a.∴ △ABC是等腰三角形.*15.设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根.请问:是否存在实数k,使得x1·x2>x1+x2成立?试说明理由.解:∵方程x2-4x+k+1=0有两个实数根,∴ Δ =16-4(k+1)≥0,∴k≤3,又x1·x2>x1+x2,而x1+x2=4,x1·x2=k+1,∴k+1>4,所以不存在实数k,使得x1·x2>x1+x2成立.即k>3,与k≤3矛盾16.已知□ABCD的两邻边AB,AD的长是关于x的方程 的两个实数根.(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;(2)若AB的长为2,那么□ABCD的周长是多少?解:∵平行四边形ABCD是菱形,∴AB=AD,∵AB、AD的长是关于x的一元二次方程 的两个实数根,解得m=1,(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;关于x的一元二次方程为 ∴当m为1时,平行四边形ABCD是菱形,且菱形的边长为 .解:将x=2代入 中,得解得∵AB、AD的长是关于x的一元二次方程的两个实数根,(2)若AB的长为2,那么□ABCD的周长是多少?C 组17.如图,一长方形地,长为x m,宽为120 m,建筑商将它分为甲、乙、丙三个区域,甲、乙为正方形.现计划甲区域建筑住宅区,乙区域建筑商场,丙区域开辟为公园.若已知丙区域的面积为3200 m2,试求x的值.3200 m2解:依题意得甲区域的边长为120m,由图可知乙区域的边长为(x-120)m.则丙区域的长为:(x-120)m 宽为:(240-x)m根据等量关系得(x-120) (240-x)=3200即x2-360x+32000=0解得 x1=160 ,x2 =200.当x=160时,丙区域的长为x-120=160-120=40(m),宽为120-40=80(m),80>40,∴x=160不符合题意,舍去. ∴x=200.18.有如下问题:“平面上,分别有2个点,3个点,4个点,5个点,…,n个点,其中任意3个点都不在一条直线上.经过每两点画一条直线,它们分别可以画多少条直线?”为了解决这一问题,小明设计了如下图表进行探究:(1)请你帮小明在图表的横线上填上归纳出的一般性结论;(2)若某人共画了171条直线,则该平面上共有多少个点?(2)若某人共画了171条直线,则该平面上共有多少个点?解:由 得n2-n-342=0.解得 n1=19 ,n2 =-18(舍去).所以平面上共有19个点.
湘教·九年级上册章末复习回顾总结一元二次方程一元二次方程的有关概念一元二次方程的应用一元二次方程的解法一元二次方程根的判别式*一元二次方程根与系数的关系配方法公式法因式分解法如果一个方程通过整理可以使右边为0,而左边是只含有一个未知数的二次多项式,那么这样的方程叫作一元二次方程,它的一般形式是ax2+bx +c=0 (a,b,c是已知数,a≠0)对于一元二次方程ax2+bx +c=0 (a,b,c是已知数,a≠0) ,其中a, b,c分别叫作二次项系数、一次项系数、常数项.配方法解一元二次方程的三种方法公式法因式分解法一元二次方程ax2+ bx +c =0 (a≠0)的根的情况可由Δ = b2- 4ac来判断:当Δ >0时,原方程有两个不相等的实数根,其根为当Δ =0时,原方程有两个相等的实数根,其根为当Δ <0时,原方程没有实数根.即当Δ≥0时,一元二次方程的根与系数之间具有如下关系:两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项与二次项系数的比.韦达定理运用一元二次方程模型解决实际问题的步骤:实际问题建立一元二次方程模型解一元二次方程一元二次方程的根实际问题的解分析数量关系设未知数检验课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(1)原方程可化为5x2- 49=0所以该方程的二次项系数是5、一次项系数是0、常数项是-49.课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(2)原方程可化为x2+3x +5=0所以该方程的二次项系数是1、一次项系数是3、常数项是5.课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(3)原方程可化为0.01t2- 5t+ 1=0所以该方程的二次项系数是0.01、一次项系数是-5、常数项是1.课堂练习A 组1.把下列方程化为一元二次方程的一般形式,并指出其中的二次项系数、一次项系数和常数项.(1) 5x2= 49; (2)6x2-7x2 =3x +5;(3) 0.01t2- 3t=2t- 1; (4)(2y-1 ) ( 2y+5 )=6y +4.解:(4)原方程可化为4y2+2y-9=0所以该方程的二次项系数是4、一次项系数是2、常数项是-9.2.解下列方程:(1) 49x2 - 144=0; (2) ( 1-x)2=1;(3)x2+8x +16=0; (4) x (7-x )=4x2;(5) x(x-2)-3x2=0; (6)x2-4x+4=64.解:原方程可化为根据平方根的意义,得因此,原方程的根为(1) 49x2 - 144=0; 解:根据平方根的意义,得因此,原方程的根为(2)(1-x)2=1解:原方程可化为根据平方根的意义,得因此,原方程的根为(3)x2+8x +16=0;解:原方程可化为5x2-7x =0.把方程左边因式分解,得x (5x -7)=0,由此得 x=0或 5x -7=0.解得 x1=0 ,x2 = .(4) x (7-x )=4x2解:原方程可化为x2+x =0.把方程左边因式分解,得x (x +1)=0,由此得 x=0或 x +1 =0.解得 x1=0 ,x2 =-1.(5) x(x-2)-3x2=0(6)x2-4x+4=64解:原方程可化为(x-2)2=64.根据平方根的意义,得因此,原方程的根为3.解下列方程:(1)2x2-6x- 3=0; (2) x (x +5)= 24;(3) x (x +1)+2 (x-1) =0; (4) (x-3)2+2x ( x -3 )=0;(5) 3(x-2)2=x (x-2).解:这里a=2,b =-6,c = -3.因而 b2-4ac = ( -6)2-4×2× (-3)=36+24=60>0,因此,原方程的根为 .所以(1)2x2-6x- 3=0(2) x (x +5)= 24解:原方程可化为x2+5x -24=0.把方程左边因式分解,得(x-3) (x +8)=0,由此得 x-3=0或 x +8 =0.解得 x1=3 ,x2 =-8.(3) x (x +1)+2 (x-1) =0解:原方程可化为因而 b2-4ac = 32-4×1× (-2)=9+8=17>0,因此,原方程的根为 .所以这里a=1,b =3,c = -2.x2+3x -2=0.(4) (x-3)2+2x ( x -3 )=0解:把方程左边因式分解,得(x-3) (x -3+2x)=0,由此得 x-3=0或 3x -3 =0,解得 x1=3 ,x2 =1.即 (x-3) (3x -3)=0(5) 3(x-2)2=x (x-2)解:原方程可化为3(x-2)2-x (x-2)=0把方程左边因式分解,得(x-2) [3(x -2)-x]=0,由此得 x-2=0或 2x -6 =0.解得 x1=2 ,x2 =3.即 (x-2) (2x -6)=04.不解方程,利用判别式判断下列方程的根的情况.(1) 4x2+6x+9=0; (2) y2=y+5.解:(1)因为Δ = b2-4ac =62-4×4×9 =36+ 144 =-108<0,所以,原方程没有实数根.解:(2)将原方程化为一般形式,得y2-y-5=0因为Δ =b2-4ac = ( -1 )2-4×1×(-5) =1+20=21>0,所以,原方程有两个不相等的实数根.(2) y2=y+5*5.设x1,x2,是方程2x2-6x+3=0的两根,求下列各式的值:(1) x1+x2; (2)x1x2; (3) x12+x22.解:*6.若方程x2-3x -1=0的两根为x1,x2,求 的值.解:由韦达定理得7.已知三个连续奇数的平方和是371,求这三个奇数.解:设三个连续奇数中间的奇数为x.由题意得(x-2)2+x2+(x+2)2=371整理,得x2=121解得 x1=11 ,x2 =-11.所以这三个奇数为9,11,13或-13,-11,-9.8.北京奥运会的主会场“鸟巢”给世人留下了深刻的记忆.据了解,在鸟巢设计的最后阶段,经过了两次优化,鸟巢的结构用钢量从最初的54000 t减少到42000 t.求平均每次用钢量降低的百分率x(精确到1%).解:根据等量关系得54000( 1-x)2=42000.整理,得 ( 1-x )2= .解得 (不合题意,舍去).答:平均每次用钢量降低的百分率为12%.9.将一块长方形桌布铺在长为1.5 m、宽为1 m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍.求桌布下垂的长度.解:设桌布下垂的长度为x m,则根据等量关系得(2x+1.5)(2x+1)=1.5×1×2整理,得 8x2+10x-3=0,解得 x1=0.25 ,x2 =-1.5(不合题意,舍去).答:桌布下垂的长度为0.25m,10.如图为一张方格纸,纸上有一三角形(上色部分),其顶点均位于网格线的交点上.若上色部分的三角形面积为15.75 cm2,则此方格纸的面积为多少?解:设每个小方格的边长为x cm.根据题意得整理,得 x2=2.25解得 x1=1.5 ,x2 =-1.5(不合题意,舍去).所以此方格纸的面积为4×1.5×4×1.5=36cm2.11.现有一块矩形钢板ABCD,长AD=7.5 m,宽AB=5 m.在这块钢板上截除两个正方形得到如图所示的模具(阴影部分所示).已知 BE= DF,且模具的面积等于原矩形钢板的面积的一半,求DF的长(精确到0.1 m).7.5 m5 mx mx m解:设DF长为x m.∵DF+FC=DC=AB=5m,∴PC=FC=(5-x)m.∵BE+EP+PC=BC=AD=7.5m,∴EP=2.5m.依题意得即 2x2-20x+25=0.解得,由于x2>5,因而舍去.答:DF长约为1.5m.12.如图,在 Rt △ABC中,∠B= 90°,AC= 10 cm,BC=6 cm.现有两点P,Q分别从点A 和点C同时出发,沿边AB,CB向终点B移动.已知点P,Q的速度分别为2 cm/s,1 cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.问是否存在这样的x,使得四边形APQC的面积等于16 cm2?若存在,请求出此时x的值;若不存在,请说明理由.解:根据题意,得AP=2x cm,CQ=x cm,假设存在这样的x,使得四边形APQC的面积等于16 cm2.∵∠B=90°,AC=10,BC=6, ∴AB=8,BQ=(6-x)cm,BP=(8-2x)cm.整理,得 x2-10x+16=0解得 x1=2 ,x2 =8.但x2 =8时不合题意,因为P从A到B只需4s.所以当x=2时,正好四边形APQC的面积等于16cm2.B 组13.解下列方程:(1)( 3x+5 )2-6 ( 3x+5 )+9=0; (2) x2+ax - 2a2=0(a为常数).解:把方程左边因式分解,得[ (3x +5)-3]2=0,由此得 (3x +5)-3=0,解得 x1=x2 = .(1)( 3x+5 )2-6 ( 3x+5 )+9=0; 解:把方程左边因式分解,得(x -a)(x+2a)=0,由此得 x-a=0或 x +2a =0,解得 x1=a,x2 = -2a.(2) x2+ax - 2a2=0(a为常数).14.已知 a,b,c分别是△ABC的三边,其中a=1,c=4,且关于x的方程x2-4x +b=0有两个相等的实数根,试判断△ABC的形状.解:依题意得关于x的方程x2-4x +b=0的判别式Δ=b2-4ac=(-4)2-4×1×b=0即 16-4b=0∴b=4=c≠a.∴ △ABC是等腰三角形.*15.设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根.请问:是否存在实数k,使得x1·x2>x1+x2成立?试说明理由.解:∵方程x2-4x+k+1=0有两个实数根,∴ Δ =16-4(k+1)≥0,∴k≤3,又x1·x2>x1+x2,而x1+x2=4,x1·x2=k+1,∴k+1>4,所以不存在实数k,使得x1·x2>x1+x2成立.即k>3,与k≤3矛盾16.已知□ABCD的两邻边AB,AD的长是关于x的方程 的两个实数根.(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;(2)若AB的长为2,那么□ABCD的周长是多少?解:∵平行四边形ABCD是菱形,∴AB=AD,∵AB、AD的长是关于x的一元二次方程 的两个实数根,解得m=1,(1)当m为何值时,□ABCD是菱形?求出这时菱形的边长;关于x的一元二次方程为 ∴当m为1时,平行四边形ABCD是菱形,且菱形的边长为 .解:将x=2代入 中,得解得∵AB、AD的长是关于x的一元二次方程的两个实数根,(2)若AB的长为2,那么□ABCD的周长是多少?C 组17.如图,一长方形地,长为x m,宽为120 m,建筑商将它分为甲、乙、丙三个区域,甲、乙为正方形.现计划甲区域建筑住宅区,乙区域建筑商场,丙区域开辟为公园.若已知丙区域的面积为3200 m2,试求x的值.3200 m2解:依题意得甲区域的边长为120m,由图可知乙区域的边长为(x-120)m.则丙区域的长为:(x-120)m 宽为:(240-x)m根据等量关系得(x-120) (240-x)=3200即x2-360x+32000=0解得 x1=160 ,x2 =200.当x=160时,丙区域的长为x-120=160-120=40(m),宽为120-40=80(m),80>40,∴x=160不符合题意,舍去. ∴x=200.18.有如下问题:“平面上,分别有2个点,3个点,4个点,5个点,…,n个点,其中任意3个点都不在一条直线上.经过每两点画一条直线,它们分别可以画多少条直线?”为了解决这一问题,小明设计了如下图表进行探究:(1)请你帮小明在图表的横线上填上归纳出的一般性结论;(2)若某人共画了171条直线,则该平面上共有多少个点?(2)若某人共画了171条直线,则该平面上共有多少个点?解:由 得n2-n-342=0.解得 n1=19 ,n2 =-18(舍去).所以平面上共有19个点.
相关资料
更多









