黑龙江省哈尔滨市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类

这是一份黑龙江省哈尔滨市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类，共35页。试卷主要包含了，与y轴交于点C，过点D向y轴作垂线，垂足为点E等内容，欢迎下载使用。
黑龙江省哈尔滨市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
一．二次函数综合题（共3小题）
1．（2022•哈尔滨）在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+b经过点A（，），点B（，﹣），与y轴交于点C．
（1）求a，b的值；
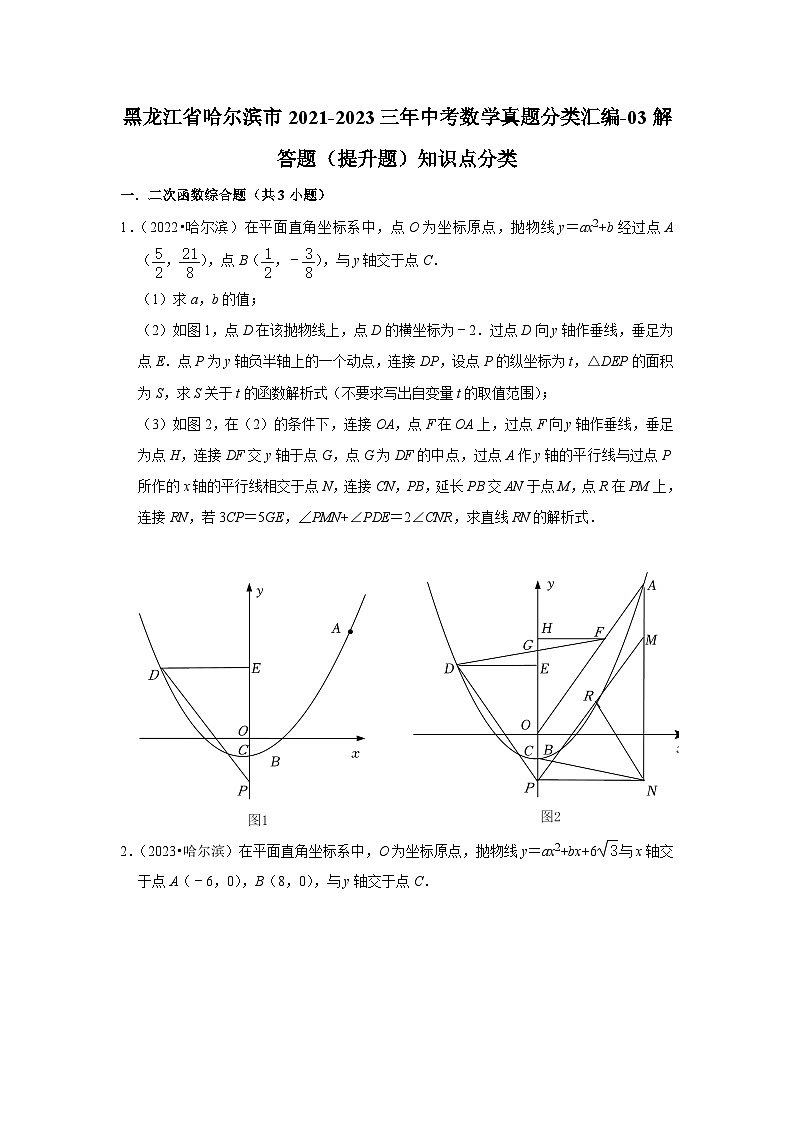
（2）如图1，点D在该抛物线上，点D的横坐标为﹣2．过点D向y轴作垂线，垂足为点E．点P为y轴负半轴上的一个动点，连接DP，设点P的纵坐标为t，△DEP的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，连接OA，点F在OA上，过点F向y轴作垂线，垂足为点H，连接DF交y轴于点G，点G为DF的中点，过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N，连接CN，PB，延长PB交AN于点M，点R在PM上，连接RN，若3CP＝5GE，∠PMN+∠PDE＝2∠CNR，求直线RN的解析式．


2．（2023•哈尔滨）在平面直角坐标系中，O为坐标原点，抛物线y＝ax2+bx+6与x轴交于点A（﹣6，0），B（8，0），与y轴交于点C．
​
（1）求a，b的值；
（2）如图①，E是第二象限抛物线上的一个动点，连接OE，CE，设点E的横坐标为t，△OCE的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图②，在（2）的条件下，当S＝6时，连接BE交y轴于点R，点F在y轴负半轴上，连接BF，点D在BF上，连接ED，点L在线段RB上（点L不与点B重合），过点L作BR的垂线与过点B且平行于ED的直线交于点G，M为LG的延长线上一点，连接BM，EG，使∠GBM＝∠BEG，P是x轴上一点，且在点B的右侧，∠PBM﹣∠GBM＝∠FRB+∠DEG，过点M作MN⊥BG，交BG的延长线于点N，点V在BG上，连接MV，使BL﹣NV＝BV，若∠EBF＝∠VMN，求直线BF的解析式．
3．（2021•哈尔滨）在平面直角坐标系中，点O为坐标系的原点，抛物线y＝ax2+bx经过A（10，0），B（，6）两点，直线y＝2x﹣4与x轴交于点C，与y轴交于点D，点P为直线y＝2x﹣4上的一个动点，连接PA．
（1）求抛物线的解析式；
（2）如图1，当点P在第一象限时，设点P的横坐标为t，△APC的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，点E在y轴的正半轴上，且OE＝OD，连接CE，当直线BP交x轴正半轴于点L，交y轴于点V时，过点P作PG∥CE交x轴于点G，过点G作y轴的平行线交线段VL于点F，连接CF，过点G作GQ∥CF交线段VL于点Q，∠CFG的平分线交x轴于点M，过点M作MH∥CF交FG于点H，过点H作HR⊥CF于点R，若FR+MH＝GQ，求点P的坐标．

二．平行四边形的性质（共1小题）
4．（2023•哈尔滨）已知四边形ABCD是平行四边形，点E在对角线BD上，点F在边BC上，连接AE，EF，DE＝BF，BE＝BC．

（1）如图①，求证△AED≌△EFB；
（2）如图②，若AB＝AD，AE≠ED，过点C作CH∥AE交BE于点H，在不添加任何辅助线的情况下，请直接写出图②中四个角（∠BAE除外），使写出的每个角都与∠BAE相等．
三．矩形的性质（共1小题）
5．（2022•哈尔滨）已知矩形ABCD的对角线AC，BD相交于点O，点E是边AD上一点，连接BE，CE，OE，且BE＝CE．
（1）如图1，求证：△BEO≌△CEO；
（2）如图2，设BE与AC相交于点F，CE与BD相交于点H，过点D作AC的平行线交BE的延长线于点G，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形（△AEF除外），使写出的每个三角形的面积都与△AEF的面积相等．


四．圆的综合题（共3小题）
6．（2023•哈尔滨）已知△ABC内接于⊙O，AB为⊙O的直径，N为的中点，连接ON交AC于点H．
​
（1）如图①，求证：BC＝2OH；
（2）如图②，点D在⊙O上，连接DB，DO，DC，DC交OH于点E，若DB＝DC，求证OD∥AC；
（3）如图③，在（2）的条件下，点F在BD上，过点F作FG⊥DO，交DO于点G，DG＝CH，过点F作FR⊥DE，垂足为R，连接EF，EA，EF：DF＝3：2，点T在BC的延长线上，连接AT，过点T作TM⊥DC，交DC的延长线于点M，若FR＝CM，AT＝4，求AB的长．
7．（2022•哈尔滨）已知CH是⊙O的直径，点A、点B是⊙O上的两个点，连接OA，OB，点D，点E分别是半径OA，OB的中点，连接CD，CE，BH，且∠AOC＝2∠CHB．
（1）如图1，求证：∠ODC＝∠OEC；
（2）如图2，延长CE交BH于点F，若CD⊥OA，求证：FC＝FH；
（3）如图3，在（2）的条件下，点G是一点，连接AG，BG，HG，OF，若AG：BG＝5：3，HG＝2，求OF的长．


8．（2021•哈尔滨）已知⊙O是△ABC的外接圆，AB为⊙O的直径，点N为AC的中点，连接ON并延长交⊙O于点E，连接BE，BE交AC于点D．
（1）如图1，求证：∠CDE+∠BAC＝135°；
（2）如图2，过点D作DG⊥BE，DG交AB于点F，交⊙O于点G，连接OG，OD，若DG＝BD，求证：OG∥AC；
（3）如图3，在（2）的条件下，连接AG，若DN＝，求AG的长．

五．作图-平移变换（共1小题）
9．（2023•哈尔滨）如图，方格纸中每个小正方形的边长均为1个单位长度，线段AB和线段CD的端点均在小正方形的顶点上．
（1）在方格纸中画出△ABE，且AB＝BE，∠ABE为钝角（点E在小正方形的顶点上）；
（2）在方格纸中将线段CD向下平移2个单位长度，再向右平移1个单位长度后得到线段MN（点C的对应点是点M，点D的对应点是点N）．连接EN，请直接写出线段EN的长．

六．条形统计图（共2小题）
10．（2023•哈尔滨）军乐中学开展以“我最喜欢的劳动实践课”为主题的调查活动，围绕“在园艺课、泥塑课、纺织课、烹饪课四门劳动实践课中，你最喜欢哪一门课？（必选且只选一门）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢泥塑课的学生人数占所调查人数的20%，请你根据图中提供的信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生？
（2）请通过计算补全条形统计图；
（3）若军乐中学共有1200名学生，请你估计该中学最喜欢烹饪课的学生共有多少名．

11．（2021•哈尔滨）春宁中学开展以“我最喜欢的冰雪运动项目”为主题的调查活动，围绕“在冰球、冰壶、短道速滑、高山滑雪四种冰雪运动项目中，你最喜欢哪一种？（必选且只选一种）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢短道速滑的学生人数占所调查人数的40%．请你根据图中提供的信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生？
（2）请通过计算补全条形统计图；
（3）若春宁中学共有1500名学生，请你估计该中学最喜欢高山滑雪的学生共有多少名．


黑龙江省哈尔滨市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
参考答案与试题解析
一．二次函数综合题（共3小题）
1．（2022•哈尔滨）在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+b经过点A（，），点B（，﹣），与y轴交于点C．
（1）求a，b的值；
（2）如图1，点D在该抛物线上，点D的横坐标为﹣2．过点D向y轴作垂线，垂足为点E．点P为y轴负半轴上的一个动点，连接DP，设点P的纵坐标为t，△DEP的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，连接OA，点F在OA上，过点F向y轴作垂线，垂足为点H，连接DF交y轴于点G，点G为DF的中点，过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N，连接CN，PB，延长PB交AN于点M，点R在PM上，连接RN，若3CP＝5GE，∠PMN+∠PDE＝2∠CNR，求直线RN的解析式．


【答案】见试题解答内容
【解答】解：（1）∵抛物线y＝ax2+b经过点A（，），点B（，﹣），
∴，
解得：，
故a＝，b＝；
（2）如图1，由（1）得：a＝，b＝，
∴抛物线的解析式为y＝x2﹣，
∵点D在该抛物线上，点D的横坐标为﹣2，
∴y＝×（﹣2）2﹣＝，
∴D（﹣2，），
∵DE⊥y轴，
∴DE＝2，
∴E（0，），
∵点P为y轴负半轴上的一个动点，且点P的纵坐标为t，
∴P（0，t），
∴PE＝﹣t，
∴S＝PE•DE＝×（﹣t）×2＝﹣t+，
故S关于t的函数解析式为S＝﹣t+；
（3）如图2，过点C作CK⊥CN，交NR的延长线于点K，过点K作KT⊥y轴于点T，
由（2）知：抛物线的解析式为y＝x2﹣，
当x＝0时，y＝﹣，
∴C（0，﹣），
∴OC＝，
∵FH⊥y轴，DE⊥y轴，
∴∠FHG＝∠DEG＝90°，
∵点G为DF的中点，
∴DG＝FG，
∵∠HGF＝∠EGD，
∴△FGH≌△DGE（AAS），
∴FH＝DE＝2，HG＝EG＝HE，
设直线OA的解析式为y＝kx，
∵A（，），
∴k＝，
解得：k＝，
∴直线OA的解析式为y＝x，
当x＝2时，y＝×2＝，
∴F（2，），
∴H（0，），
∴HE＝﹣＝，
∴GE＝HE＝×＝，
∵3CP＝5GE，
∴CP＝GE＝×＝，
∴P（0，﹣1），
∵AN∥y轴，PN∥x轴，
∴N（，﹣1），
∴PN＝，
∵E（0，），
∴EP＝﹣（﹣1）＝，
设直线BP的解析式为y＝mx+n，则，
解得：，
∴直线BP的解析式为y＝x﹣1，
当x＝时，y＝×﹣1＝，
∴M（，），
∴MN＝﹣（﹣1）＝，
∵＝＝，＝＝，
∴＝，
又∵∠PNM＝∠DEP＝90°，
∴△PMN∽△DPE，
∴∠PMN＝∠DPE，
∵∠DPE+∠PDE＝90°，
∴∠PMN+∠PDE＝90°，
∵∠PMN+∠PDE＝2∠CNR，
∴∠CNR＝45°，
∵CK⊥CN，
∴∠NCK＝90°，
∴△CNK是等腰直角三角形，
∴CK＝CN，
∵∠CTK＝∠NPC＝90°，
∴∠KCT+∠CKT＝90°，
∵∠NCP+∠KCT＝90°，
∴∠CKT＝∠NCP，
∴△CKT≌△NCP（AAS），
∴CT＝PN＝，KT＝CP＝，
∴OT＝CT﹣OC＝﹣＝2，
∴K（，2），
设直线RN的解析式为y＝ex+f，把K（，2），N（，﹣1）代入，
得：，
解得：，
∴直线RN的解析式为y＝﹣x+．


2．（2023•哈尔滨）在平面直角坐标系中，O为坐标原点，抛物线y＝ax2+bx+6与x轴交于点A（﹣6，0），B（8，0），与y轴交于点C．
​
（1）求a，b的值；
（2）如图①，E是第二象限抛物线上的一个动点，连接OE，CE，设点E的横坐标为t，△OCE的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图②，在（2）的条件下，当S＝6时，连接BE交y轴于点R，点F在y轴负半轴上，连接BF，点D在BF上，连接ED，点L在线段RB上（点L不与点B重合），过点L作BR的垂线与过点B且平行于ED的直线交于点G，M为LG的延长线上一点，连接BM，EG，使∠GBM＝∠BEG，P是x轴上一点，且在点B的右侧，∠PBM﹣∠GBM＝∠FRB+∠DEG，过点M作MN⊥BG，交BG的延长线于点N，点V在BG上，连接MV，使BL﹣NV＝BV，若∠EBF＝∠VMN，求直线BF的解析式．
【答案】（1）a＝﹣，b＝；
（2）S＝﹣3t；
（3）y＝x﹣．
【解答】解：（1）将点A（﹣6，0），B（8，0）代入y＝ax2+bx+6，
，
解得；
（2）由（1）可知抛物线的解析式为y＝﹣x2+x+6，
当x＝0时，y＝6，
∴C（0，6），
∴OC＝6，
∴S＝（﹣t）×6＝﹣3t；
（3）∵S＝6，
∴﹣3t＝6，
解得t＝﹣2，
∴E（﹣2，5），
如图：以BM为一边作∠MBT＝∠MBN，∠MBT的另一边BT交LM的延长线于点T，
∵ED∥BG，
∴∠DEB＝∠EBG，
∵∠GEB＝2∠GBM，
∴∠GEB＝∠GBT，
∴∠DEB+∠GEB＝∠EBG+∠GBT，
∴∠DEG＝∠EBT，
∵∠PBM﹣∠GBM＝∠FRB+∠DEG，∠PBM﹣∠GBM＝∠TBP，∠ROB＝90°，
∴∠TBP＝90°﹣∠RBO+∠EBT，
∵∠RBO+∠EBT+∠TBP＝180°，
∴∠EBT＝60°，
∵LG⊥EB，
∴∠GLB＝90°，
∴∠T＝30°，
∴LB＝BT，
作MK⊥BT，
∵MN⊥GB，
∴∠MKT＝∠N＝∠MKB＝90°，
∵MB＝MB，
∴△MNB≌△MKB（AAS），
∴NB＝BK，MN＝MK，
∵BL﹣NV＝BV，
∴2BL﹣2NV＝BV，
∴BT﹣NV＝BV+NV＝BN＝BK，
∴BT﹣BK＝NV＝KT，
∴Rt△NMV≌Rt△KMT（HL），
∴∠T＝∠NVM＝30°，
∴∠NMV＝60°，
∵∠EBF＝∠VMN，
∴∠EBF＝60°，
作FS⊥BE交于S点，作EQ⊥x轴交于Q点，
∴∠EQB＝∠RSF＝∠BSF＝90°，
∵B（8，0），
∴OB＝8，
∵E（﹣2，5），
∴EQ＝5，QB＝10，
∵tan∠EBQ＝＝，
∴＝，
解得OR＝4，
∴BR＝＝4，
∵tan∠FRB＝＝＝＝，tan∠FBS＝tan60°＝＝，
∴设FS＝2m，则RS＝3m，BS＝2m，
∴3m+2m＝4，
解得m＝，
∵RF＝＝m＝，
∴OF＝，
∴F（0，﹣），
设直线BF的解析式为y＝kx+c，
∴，
解得，
∴直线BF的解析式为y＝x﹣．

3．（2021•哈尔滨）在平面直角坐标系中，点O为坐标系的原点，抛物线y＝ax2+bx经过A（10，0），B（，6）两点，直线y＝2x﹣4与x轴交于点C，与y轴交于点D，点P为直线y＝2x﹣4上的一个动点，连接PA．
（1）求抛物线的解析式；
（2）如图1，当点P在第一象限时，设点P的横坐标为t，△APC的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，点E在y轴的正半轴上，且OE＝OD，连接CE，当直线BP交x轴正半轴于点L，交y轴于点V时，过点P作PG∥CE交x轴于点G，过点G作y轴的平行线交线段VL于点F，连接CF，过点G作GQ∥CF交线段VL于点Q，∠CFG的平分线交x轴于点M，过点M作MH∥CF交FG于点H，过点H作HR⊥CF于点R，若FR+MH＝GQ，求点P的坐标．

【答案】（1）y＝﹣x2+x．
（2）S＝8t﹣16．
（3）P（，5）．
【解答】解：（1）把A（10，0），B（，6）代入y＝ax2+bx，得到，
解得，
∴抛物线的解析式为y＝﹣x2+x．

（2）∵直线y＝2x﹣4与x轴交于点C，与y轴交于点D，
∴C（2，0），D（0，﹣4），
∵A（10，0），
∴OA＝10，OC＝2，
∴AC＝8，
由题意P（t，2t﹣4），
∴S＝•PT•AC＝×8×（2t﹣4）＝8t﹣16．

（3）如图2中，过点P作PT⊥CG于T，交CF于W，过点F作FJ⊥MH交MH的延长线于J，连接JQ．

∵PT⊥CG，
∴∠PTC＝∠ODC＝90°，
∴OD∥PT，
∴∠ODC＝∠CPT，
∴tan∠CPT＝tan∠ODC＝＝＝，
∵HR⊥RF，FJ⊥MJ，MH∥CF，
∴RH⊥MJ，
∴∠FRH＝∠RHJ＝∠FJH＝90°，
∴四边形RFJH是矩形，
∴RF＝HJ，
∵RF+HM＝MH+HJ＝MJ＝GQ，MJ∥GQ，
∴四边形MJQG是平行四边形，
∴JQ＝GM，∠JQG＝∠GMJ，
∵MF平分∠CFG，
∴∠CFM＝∠MFG，
∵CF∥MH，
∴∠FMH＝∠CFM，
∴∠FMH＝∠MFH，
∴FH＝HM，
∵∠MGH＝∠FJH＝90°，∠MHG＝∠FHJ，
∴△MHG≌△FHJ（AAS），
∴MG＝FJ＝JQ，∠GMH＝∠HFJ，
∴∠JFQ＝∠JQF，∠GFJ＝∠GQJ，
∴∠GFQ＝∠GQF，
∵CF∥GQ，PT∥FG，
∴∠WPF＝∠GFQ，∠WFP＝∠GQF，
∴∠WPF＝∠WFP，
∴WP＝WF，
∵D，E关于x轴对称，
∴∠ECO＝∠DCO＝∠PCG，
∵EC∥PG，
∴∠PGC＝∠ECO，
∴∠PCG＝∠PGC，
∴PC＝PG，
∵PT⊥CG，
∴CT＝TG，
∵WT∥FG，
∴CW＝WF，
∴WP＝WC＝WF，
∴∠CPF＝90°，
∴∠LCP+∠PLC＝90°，
∵∠ODC+∠OCD＝90°，∠OCD＝∠LCP，
∴∠PLC＝∠ODC，
∴tan∠PLC＝tan∠ODC＝，
∵B（，6），
∴OL＝+12＝，
∴L（，0），
∴直线PB的解析式为y＝﹣x+，
由，解得，
∴P（，5）．
二．平行四边形的性质（共1小题）
4．（2023•哈尔滨）已知四边形ABCD是平行四边形，点E在对角线BD上，点F在边BC上，连接AE，EF，DE＝BF，BE＝BC．

（1）如图①，求证△AED≌△EFB；
（2）如图②，若AB＝AD，AE≠ED，过点C作CH∥AE交BE于点H，在不添加任何辅助线的情况下，请直接写出图②中四个角（∠BAE除外），使写出的每个角都与∠BAE相等．
【答案】（1）证明见解析；
（2）∠AEB，∠DHC，∠EFC，∠DCH．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴∠ADE＝∠EBF，
∵BC＝BE，
∴AD＝BE，
在△AED和△EFB中，
，
∴△AED≌△EFB（SAS）；
（2）解：∵四边形ABCD是平行四边形，
∴AD＝BC，AB∥CD，
∵AB＝AD，
∴AB＝BC，
∵BE＝BC，
∴AB＝BE，
∴∠BEA＝∠BAE，
∵CH∥AE，
∴∠DHC＝∠BEA，
∵AB∥CD，
∴∠CDH＝∠ABE，
∴∠DCH＝∠BAE，
∵△AED≌△EFB（SAS），
∴∠AED＝∠EFB，
∴∠EFC＝∠AEB，
∴与∠BAE相等角是∠AEB，∠DHC，∠EFC，∠DCH．
三．矩形的性质（共1小题）
5．（2022•哈尔滨）已知矩形ABCD的对角线AC，BD相交于点O，点E是边AD上一点，连接BE，CE，OE，且BE＝CE．
（1）如图1，求证：△BEO≌△CEO；
（2）如图2，设BE与AC相交于点F，CE与BD相交于点H，过点D作AC的平行线交BE的延长线于点G，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形（△AEF除外），使写出的每个三角形的面积都与△AEF的面积相等．


【答案】见试题解答内容
【解答】（1）证明：∵四边形ABCD是矩形，
∴OA＝OC＝AC，OB＝OD＝BD，AC＝BD，
∴OB＝OC＝OA＝OD，
∵BE＝CE，OE＝OE，
∴△BEO≌△CEO（SSS）；
（2）解：△DHE，△CHO，△DEG，△BFO都与△AEF的面积相等，
理由：∵四边形ABCD是矩形，
∴∠BAD＝∠CDA＝90°AB∥CD，AB＝DC，
∵BE＝CE，
∴Rt△BAE≌Rt△CDE（HL），
∴∠AEB＝∠DEC，AE＝DE，
∵OA＝OD，
∴∠OEA＝∠OED＝90°，
∴∠BAD＝∠OED＝90°，∠ADC＝∠AEO＝90°，
∴AB∥OE，DC∥OE，
∴△AEO的面积＝△BEO的面积，△DEO的面积＝△COE的面积，
∴△AEO的面积﹣△EFO的面积＝△BEO的面积﹣△EFO的面积，△DEO的面积﹣△EHO的面积＝△COE的面积﹣△EHO的面积，
∴△AEF的面积＝△BFO的面积，△DHE的面积＝△CHO的面积，
∵OA＝OD，
∴∠DAO＝∠ADO，
∴△AEF≌△DEH（ASA），
∴△AEF的面积＝△DHE的面积＝△CHO的面积，
∵DG∥AC，
∴∠G＝∠AFE，∠GDE＝∠FAE，
∴△AEF≌△DEG（AAS），
∴△AEF的面积＝△DEG的面积，
∴△DHE，△CHO，△DEG，△BFO都与△AEF的面积相等．
四．圆的综合题（共3小题）
6．（2023•哈尔滨）已知△ABC内接于⊙O，AB为⊙O的直径，N为的中点，连接ON交AC于点H．
​
（1）如图①，求证：BC＝2OH；
（2）如图②，点D在⊙O上，连接DB，DO，DC，DC交OH于点E，若DB＝DC，求证OD∥AC；
（3）如图③，在（2）的条件下，点F在BD上，过点F作FG⊥DO，交DO于点G，DG＝CH，过点F作FR⊥DE，垂足为R，连接EF，EA，EF：DF＝3：2，点T在BC的延长线上，连接AT，过点T作TM⊥DC，交DC的延长线于点M，若FR＝CM，AT＝4，求AB的长．
【答案】（1）见解析；
（2）见解析；
（3）2．
【解答】（1）证明：如图①，连接OC，
∵N是的中点，
∴＝，
∴∠AON＝∠CON，
∵OA＝OC，
∴AH＝HC，
∵OA＝OB，
∴OH是△ABC的中位线，
∴BC＝2OH；
（2）证明：如图②，设∠BDC＝2α，
∵BD＝CD，DO＝DO，BO＝OC，
∴△DOB≌△DOC（SSS），
∴∠BDO＝∠CDO＝∠BDC＝α，
∵OB＝OD，
∴∠DBO＝∠BDO＝α，
∵∠ACD＝∠ABD＝α，
∴∠CDO＝∠ACD，
∴DO∥AC；
（3）解：如图③，连接AD，延长AE与BC交于W点，延长AC、TM交于L点，
∵FG⊥OD，
∴∠DGF＝90°，
∵∠CHE＝90°，
∴∠DGF＝∠CHE，
∵∠FDG＝∠ECH，DG＝CH，
∴△DGF≌△CHE（AAS），
∴DF＝CE，
∵AH＝CH，
∴OH⊥AC，
∴∠EHC＝∠DGF，
∵AH＝HC，
∴△AEC是等腰三角形，
∴AE＝EC，∠EAC＝∠ECA，
∵∠BDO＝∠ODE＝∠ECA，
∴∠EAH＝∠FDG，
∵DG＝CH，
∴DG＝AH，
∴△DFG≌△AFH（ASA），
∴AE＝DF，
∵∠DEA＝2∠ECA，∠FDE＝2∠ODE，
∴∠FDE＝∠DEA，
∴DF∥AE，
∴四边形AEFD是平行四边形，
∵AB是圆O的直径，
∴∠ADB＝90°，
∴四边形ADFE是矩形，
∴EF⊥BD，
∵EF：DF＝3：2，
∴tan∠EDF＝，
∵FR⊥CD，FG⊥DO，
∴∠ODE＝∠RFK＝90°，
∵∠ECA＝∠MCL，
∴∠RFK＝∠LCM，
∵CM⊥MT，
∴∠CML＝90°，
∵FR＝CM，
∴△FRK≌△CML（AAS），
∴CL＝FK＝2FG，
∵BC＝2OH，EH＝OH，
∴EH是△AWC的中位线，
∴CW＝2EH，
∵EH＝FG，
∴CL＝FK＝2FG＝CW，
∵∠TCL＝∠CMT＝90°，
∴∠MCL＝∠CTM，
∵∠ACE＝∠ECA＝∠LCM，
∴∠CTM＝∠WAC，
∴△AWC≌△TLC（AAS），
∴AC＝TC，
在Rt△ACT中，AT＝4，
∴AC＝CT＝4，
∵AW∥BD，
∴∠BAW＝∠DBC，
∵∠DBO＝∠BDO，∠EAC＝∠BDO＝∠ODE，
∴∠BAC＝∠BDE，
在Rt△ABC中，tan∠BAC＝＝，
∴BC＝6，
在Rt△ABC中，AB＝＝2．



7．（2022•哈尔滨）已知CH是⊙O的直径，点A、点B是⊙O上的两个点，连接OA，OB，点D，点E分别是半径OA，OB的中点，连接CD，CE，BH，且∠AOC＝2∠CHB．
（1）如图1，求证：∠ODC＝∠OEC；
（2）如图2，延长CE交BH于点F，若CD⊥OA，求证：FC＝FH；
（3）如图3，在（2）的条件下，点G是一点，连接AG，BG，HG，OF，若AG：BG＝5：3，HG＝2，求OF的长．


【答案】见试题解答内容
【解答】（1）证明：如图1，∵点D，点E分别是半径OA，OB的中点，
∴OD＝OA，OE＝OB，
∵OA＝OB，
∴OE＝OD，
∵∠AOC＝2∠CHB，∠BOC＝2∠CHB，
∴∠AOC＝∠BOC，
∵OC＝OC，
∴△OCD≌△OCE（SAS），
∴∠ODC＝∠OEC；
（2）证明：∵CD⊥OA，
∴∠CDO＝90°，
由（1）知：∠ODC＝∠OEC＝90°，
∴sin∠OCE＝＝，
∴∠OCE＝30°，
∴∠COE＝60°，
∵∠H＝∠COE＝30°，
∴∠H＝∠OCE，
∴FC＝FH；
（3）解：∵CO＝OH，FC＝FH，
∴FO⊥CH，
∴∠FOH＝90°，
如图，连接AH，
∵∠AOC＝∠BOC＝60°，
∴∠AOH＝∠BOH＝120°，
∴AH＝BH，∠AGH＝60°，
∵AG：BG＝5：3，
∴设AG＝5x，BG＝3x，
在AG上取点M，使得AM＝BG，连接MH，过点H作HN⊥GM于N，

∵∠HAM＝∠HBG，
∴△HAM≌△HBG（SAS），
∴MH＝GH，
∴△MHG是等边三角形，
∴MG＝HG＝2，
∵AG＝AM+MG，
∴5x＝3x+2，
∴x＝1，
∴AG＝5，BG＝AM＝3，
∴MN＝GM＝×2＝1，HN＝，
∴AN＝MN+AM＝4，
∴HB＝HA＝＝＝，
∵∠FOH＝90°，∠OHF＝30°，
∴∠OFH＝60°，
∵OB＝OH，
∴∠BHO＝∠OBH＝30°，
∴∠FOB＝∠OBF＝30°，
∴OF＝BF，
在Rt△OFH中，∠OHF＝30°，
∴HF＝2OF，
∴HB＝BF+HF＝3OF＝，
∴OF＝．
8．（2021•哈尔滨）已知⊙O是△ABC的外接圆，AB为⊙O的直径，点N为AC的中点，连接ON并延长交⊙O于点E，连接BE，BE交AC于点D．
（1）如图1，求证：∠CDE+∠BAC＝135°；
（2）如图2，过点D作DG⊥BE，DG交AB于点F，交⊙O于点G，连接OG，OD，若DG＝BD，求证：OG∥AC；
（3）如图3，在（2）的条件下，连接AG，若DN＝，求AG的长．

【答案】（1）证明见解答；
（2）证明见解答；
（3）2．
【解答】（1）证明：如图1，过点O作OP⊥BC，交⊙O于点P，连接AP交BE于Q，

∴＝，
∴∠BAP＝∠CAP，
∵点N为AC的中点，
∴＝，
∴∠ABE＝∠CBE，
∵AB是⊙O的直径，
∴∠C＝90°，
∴∠BAC+∠ABC＝90°，
∴∠QAB+∠QBA＝×90°＝45°，
∴∠AQB＝∠EQP＝135°，
△AQD中，∠EQP＝∠CAP+∠ADQ＝135°，
∴∠CDE+∠BAC＝135°；
（2）证明：在△DGO和△DBO中，
，
∴△DGO≌△DBO（SSS），
∴∠ABD＝∠DGO，
∵DG⊥BE，
∴∠GDB＝90°，
∴∠ADG+∠BDC＝90°，
∵∠BDC+∠CBE＝90°，
∴∠ADG＝∠CBE＝∠ABD＝∠DGO，
∴OG∥AD；
（3）解：如图3，过点G作GK⊥AC于K，延长GO交BC于点H，

由（2）知：OG∥AC，
∴GH∥AC，
∴∠OHB＝∠C＝90°，
∴OH⊥BC，
∴BH＝CH，
∵∠K＝∠C＝∠OHC＝90°，
∴四边形GHCK是矩形，
∴CH＝GK，
设GK＝y，则BC＝2y，ON＝GK＝y，
由（2）知：∠ADG＝∠DBC，
在△GKD和△DCB中，
，
∴△GKD≌△DCB（AAS），
∴GK＝DC＝y，
∵OE∥BC，
∴∠E＝∠DBC，
∴tan∠DBC＝tanE，
∴，即＝，
∴EN＝，
∴AN＝CN＝y+，ON＝y，
由勾股定理得：AO2＝ON2+AN2，
∴（y+）2＝y2+（y+）2，
解得：y1＝﹣（舍），y2＝，
∴AG＝＝＝2．
五．作图-平移变换（共1小题）
9．（2023•哈尔滨）如图，方格纸中每个小正方形的边长均为1个单位长度，线段AB和线段CD的端点均在小正方形的顶点上．
（1）在方格纸中画出△ABE，且AB＝BE，∠ABE为钝角（点E在小正方形的顶点上）；
（2）在方格纸中将线段CD向下平移2个单位长度，再向右平移1个单位长度后得到线段MN（点C的对应点是点M，点D的对应点是点N）．连接EN，请直接写出线段EN的长．

【答案】（1）作图见解析部分；
（2）作图见解析部分，．
【解答】解：（1）如图，△ABE即为所求；
（2）如图，线段MN即为所求，EN＝＝．

六．条形统计图（共2小题）
10．（2023•哈尔滨）军乐中学开展以“我最喜欢的劳动实践课”为主题的调查活动，围绕“在园艺课、泥塑课、纺织课、烹饪课四门劳动实践课中，你最喜欢哪一门课？（必选且只选一门）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢泥塑课的学生人数占所调查人数的20%，请你根据图中提供的信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生？
（2）请通过计算补全条形统计图；
（3）若军乐中学共有1200名学生，请你估计该中学最喜欢烹饪课的学生共有多少名．

【答案】（1）50；
（2）见解析；
（3）480名．
【解答】解：（1）10÷20%＝50（名），
答：在这次调查中，一共抽取了50名学生；
（2）喜欢纺织课的人数为：50﹣15﹣10﹣20＝5（名），
补全条形统计图如下：

（3）1200×＝480（名），
答：估计该中学最喜欢烹饪课的学生共有480名．
11．（2021•哈尔滨）春宁中学开展以“我最喜欢的冰雪运动项目”为主题的调查活动，围绕“在冰球、冰壶、短道速滑、高山滑雪四种冰雪运动项目中，你最喜欢哪一种？（必选且只选一种）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢短道速滑的学生人数占所调查人数的40%．请你根据图中提供的信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生？
（2）请通过计算补全条形统计图；
（3）若春宁中学共有1500名学生，请你估计该中学最喜欢高山滑雪的学生共有多少名．

【答案】见试题解答内容
【解答】解：（1）本次调查共抽取的学生数有：24÷40%＝60（名）；

（2）最喜欢冰壶项目的人数有：60﹣16﹣24﹣12＝8（名），补全统计图如下：


（3）根据题意得：
1500×＝300（名），
答：估计该中学最喜欢高山滑雪的学生共有300名．