

江苏省各地市2023年中考数学真题分类汇编-03解答题基础题知识点分类
展开江苏省各地市2023年中考数学真题分类汇编-03解答题基础题知识点分类
一.实数的运算(共1小题)
1.(2023•连云港)计算|﹣4|+(π﹣)0﹣()﹣1.
二.分式的化简求值(共1小题)
2.(2023•苏州)先化简,再求值:•﹣,其中a=.
三.解二元一次方程组(共1小题)
3.(2023•连云港)解方程组.
四.解一元一次不等式组(共2小题)
4.(2023•扬州)解不等式组并把它的解集在数轴上表示出来.
5.(2023•苏州)解不等式组:.
五.反比例函数与一次函数的交点问题(共1小题)
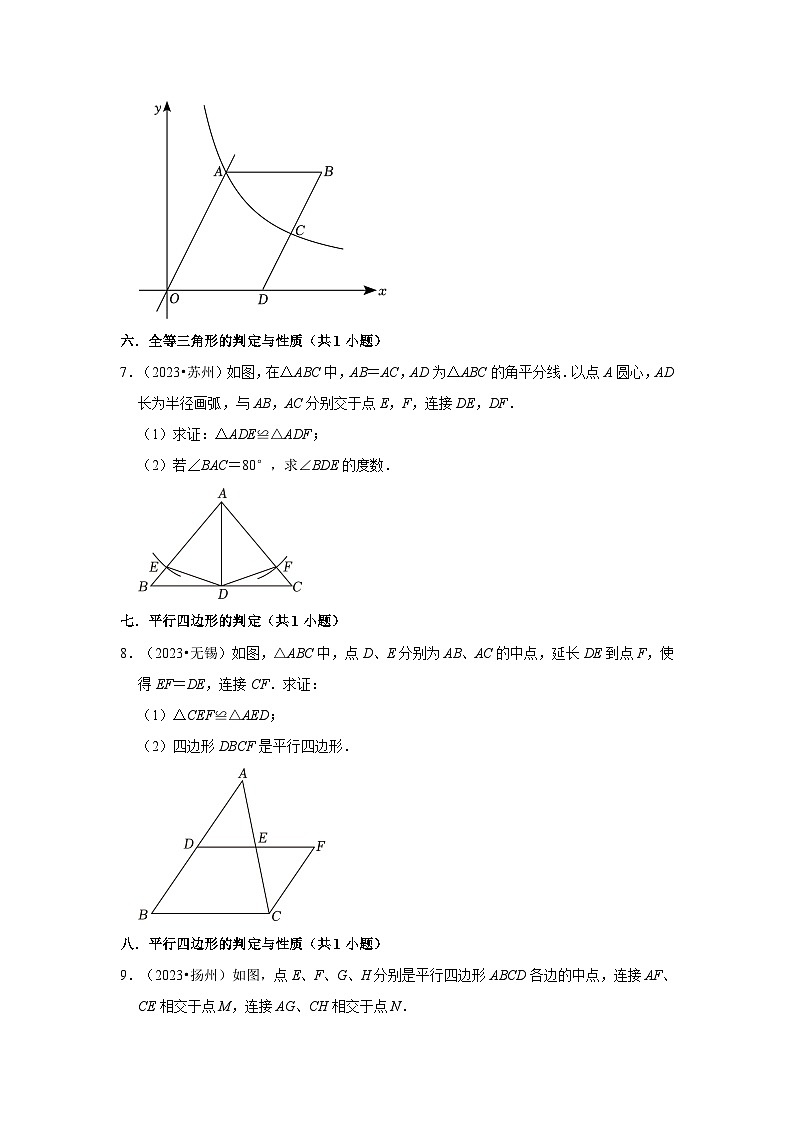
6.(2023•苏州)如图,一次函数y=2x的图象与反比例函数y=(x>0)的图象交于点A(4,n).将点A沿x轴正方向平移m个单位长度得到点B,D为x轴正半轴上的点,点B的横坐标大于点D的横坐标,连接BD,BD的中点C在反比例函数y=(x>0)的图象上.
(1)求n,k的值;
(2)当m为何值时,AB•OD的值最大?最大值是多少?
六.全等三角形的判定与性质(共1小题)
7.(2023•苏州)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.
(1)求证:△ADE≌△ADF;
(2)若∠BAC=80°,求∠BDE的度数.
七.平行四边形的判定(共1小题)
8.(2023•无锡)如图,△ABC中,点D、E分别为AB、AC的中点,延长DE到点F,使得EF=DE,连接CF.求证:
(1)△CEF≌△AED;
(2)四边形DBCF是平行四边形.
八.平行四边形的判定与性质(共1小题)
9.(2023•扬州)如图,点E、F、G、H分别是平行四边形ABCD各边的中点,连接AF、CE相交于点M,连接AG、CH相交于点N.
(1)求证:四边形AMCN是平行四边形;
(2)若▱AMCN的面积为4,求▱ABCD的面积.
九.圆周角定理(共1小题)
10.(2023•无锡)如图,AB是⊙O的直径,FD为⊙O的切线,CD与AB相交于点E.DF∥AB,交CA的延长线于点F,CF=CD.
(1)求∠F 的度数;
(2)若 DE•DC=8,求⊙O的半径.
一十.直线与圆的位置关系(共1小题)
11.(2023•扬州)如图,在△ABC中,∠ACB=90°,点D是AB上一点,且∠BCD=∠A,点O在BC上,以点O为圆心的圆经过C、D两点.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若sinB=,⊙O的半径为3,求AC的长.
一十一.命题与定理(共1小题)
12.(2023•泰州)如图,CD是五边形ABCDE的一边,若AM垂直平分CD,垂足为M,且 , ,则 .
给出下列信息:①AM平分∠BAE;②AB=AE;③BC=DE.请从中选择适当信息,将对应的序号填到横线上方,使之构成真命题,补全图形,并加以证明.
一十二.用样本估计总体(共1小题)
13.(2023•泰州)如图是我国2019~2022年汽车销售情况统计图.
根据图中信息,解答下列问题:
(1)2022年我国新能源汽车销售量约占该年各类汽车销售总量的 %(精确到1%);这4年中,我国新能源汽车销售量在各类汽车销售总量占比最高的年份是 年;
(2)小明说:新能源汽车2022年的销售量超过前3年的总和,所以2022年新能源汽车销售量的增长率比2021年高.你同意他的说法吗?请结合统计图说明你的理由.
一十三.条形统计图(共1小题)
14.(2023•苏州)某初中学校为加强劳动教育,开设了劳动技能培训课程.为了解培训效果,学校对七年级320名学生在培训前和培训后各进行一次劳动技能检测,两次检测项目相同,评委依据同一标准进行现场评估,分成“合格”、“良好”、“优秀”3个等级,依次记为2分、6分、8分(比如,某同学检测等级为“优秀”,即得8分).学校随机抽取32名学生的2次检测等级作为样本,绘制成如图的条形统计图:
(1)这32名学生在培训前得分的中位数对应等级应为 ;(填“合格”、“良好”或“优秀”)
(2)求这32名学生培训后比培训前的平均分提高了多少?
(3)利用样本估计该校七年级学生中,培训后检测等级为“良好”与“优秀”的学生人数之和是多少?
一十四.列表法与树状图法(共2小题)
15.(2023•泰州)某校组织学生去敬老院表演节目,表演形式有舞蹈、情景剧和唱歌3种类型.小明、小丽2人积极报名参加,从3种类型中随机挑选一种类型.求小明、小丽选择不同类型的概率.
16.(2023•扬州)扬州是个好地方,有着丰富的旅游资源.某天甲、乙两人来扬州旅游,两人分别从A、B、C三个景点中随机选择一个景点游览.
(1)甲选择A景点的概率为 ;
(2)请用画树状图或列表的方法,求甲、乙两人中至少有一人选择C景点的概率.
江苏省各地市2023年中考数学真题分类汇编-03解答题基础题知识点分类
参考答案与试题解析
一.实数的运算(共1小题)
1.(2023•连云港)计算|﹣4|+(π﹣)0﹣()﹣1.
【答案】3.
【解答】解:原式=4+1﹣2
=5﹣2
=3.
二.分式的化简求值(共1小题)
2.(2023•苏州)先化简,再求值:•﹣,其中a=.
【答案】,﹣1.
【解答】解:原式=•﹣
=﹣
=
=,
当a=时,
原式=
=﹣1.
三.解二元一次方程组(共1小题)
3.(2023•连云港)解方程组.
【答案】.
【解答】解:,
①+②得:5x=15,
解得:x=3,
将x=3代入①得:3×3+y=8,
解得:y=﹣1,
故原方程组的解为:.
四.解一元一次不等式组(共2小题)
4.(2023•扬州)解不等式组并把它的解集在数轴上表示出来.
【答案】﹣1<x≤2,解集在数轴上表示见解答.
【解答】解:,
解不等式①得:x>﹣1,
解不等式②得:x≤2,
∴原不等式组的解集为:﹣1<x≤2,
∴该不等式组的解集在数轴上表示如图所示:
5.(2023•苏州)解不等式组:.
【答案】.
【解答】解:解不等式2x+1>0得x>﹣,
解不等式 得x<2.
∴不等式组的解集是 .
五.反比例函数与一次函数的交点问题(共1小题)
6.(2023•苏州)如图,一次函数y=2x的图象与反比例函数y=(x>0)的图象交于点A(4,n).将点A沿x轴正方向平移m个单位长度得到点B,D为x轴正半轴上的点,点B的横坐标大于点D的横坐标,连接BD,BD的中点C在反比例函数y=(x>0)的图象上.
(1)求n,k的值;
(2)当m为何值时,AB•OD的值最大?最大值是多少?
【答案】(1)8,32;(2)6,36.
【解答】解:(1)将点A(4,n)代入y=2x,得:n=8,
∴点A的坐标为(4,8),
将点A(4,8)代入,得:k=32.
(2)∵点B的横坐标大于点D的横坐标,
∴点B在点D的右侧.
过点C作直线EF⊥x轴于F,交AB于E,
由平移的性质得:AB∥x轴,AB=m,
∴∠B=∠CDF,
∵点C为BD的中点,
∴BC=DC,
在△ECB和△FCD中,
,
∴△ECB≌△FCD(ASA),
∴BE=DF,CE=CF.
∵AB∥x轴,点A的坐标为(4,8),
∴EF=8,
∴CE=CF=4,
∴点C的纵坐标为4,
由(1)知:反比例函数的解析式为:,
∴当y=4时,x=8,
∴点C的坐标为(8,4),
∴点E的坐标为(8,8),点F的坐标为(8,0),
∵点A(4,8),AB=m,AB∥x轴,
∴点B的坐标为(m+4,8),
∴BE=m+4﹣8=m﹣4,
∴DF=BE=m﹣4,
∴OD=8﹣(m﹣4)=12﹣m
AB•OD=m(12﹣m)=﹣(m﹣6)2+36
∴当 m=6时,AB•OD取得最大值,最大值为36.
六.全等三角形的判定与性质(共1小题)
7.(2023•苏州)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.
(1)求证:△ADE≌△ADF;
(2)若∠BAC=80°,求∠BDE的度数.
【答案】(1)证明见解析;
(2)20°.
【解答】(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
由作图知:AE=AF.
在△ADE和△ADF中,
,
∴△ADE≌△ADF(SAS);
(2)解:∵∠BAC=80°,AD为△ABC的角平分线,
∴∠EAD=∠BAC=40°,
由作图知:AE=AD.
∴∠AED=∠ADE,
∴∠ADE=×(180°﹣40°)=70°,
∵AB=AC,AD为△ABC的角平分线,
∴AD⊥BC.
∴∠BDE=90°﹣∠ADE=20°.
七.平行四边形的判定(共1小题)
8.(2023•无锡)如图,△ABC中,点D、E分别为AB、AC的中点,延长DE到点F,使得EF=DE,连接CF.求证:
(1)△CEF≌△AED;
(2)四边形DBCF是平行四边形.
【答案】(1)见解析;
(2)见解析.
【解答】证明:(1)∵点D、E分别为AB、AC的中点,
∴AE=CE,
在△CEF与△AED中,
,
∴△CEF≌△AED(SAS);
(2)由(1)证得△CEF≌△AED,
∴∠A=∠FCE,
∴BD∥CF,
∵DF∥BC,
∴四边形DBCF是平行四边形.
八.平行四边形的判定与性质(共1小题)
9.(2023•扬州)如图,点E、F、G、H分别是平行四边形ABCD各边的中点,连接AF、CE相交于点M,连接AG、CH相交于点N.
(1)求证:四边形AMCN是平行四边形;
(2)若▱AMCN的面积为4,求▱ABCD的面积.
【答案】(1)见解析过程;
(2)12.
【解答】解:(1)∵点E、F、G、H分别是平行四边形ABCD各边的中点,
∴AH∥CF,AH=CF,
∴四边形AFCH是平行四边形,
∴AM∥CN,
同理可得,四边形AECG是平行四边形,
∴AN∥CM,
∴四边形AMCN是平行四边形;
(2)如图所示,连接AC,
∵H,G分别是AD,CD的中点,
∴点N是△ACD的重心,
∴CN=2HN,
∴S△ACN=S△ACH,
又∵CH是△ACD的中线,
∴S△ACN=S△ACD,
又∵AC是平行四边形AMCN和平行四边形ABCD的对角线,
∴S平行四边形AMCN=S平行四边形ABCD,
又∵▱AMCN的面积为4,
∴▱ABCD的面积为12.
九.圆周角定理(共1小题)
10.(2023•无锡)如图,AB是⊙O的直径,FD为⊙O的切线,CD与AB相交于点E.DF∥AB,交CA的延长线于点F,CF=CD.
(1)求∠F 的度数;
(2)若 DE•DC=8,求⊙O的半径.
【答案】(1)67.5°;
(2)2.
【解答】解:(1)如图,连接OD,
∵FD为⊙O的切线,
∴∠ODF=90°,
∵DF∥AB,
∴∠AOD=180°﹣∠ODF=90°,
∴∠ACD=∠AOD=45°,
∵CF=CD,
∴∠F=∠CDF==67.5°;
(2)∵OA=OD,∠AOD=90°,
∴∠EAD=45°,
∵∠ACD=45°,
∴∠ACD=∠EAD,
∵∠ADE=∠CDA,
∴△DAE∽△DCA,
∴=,
∴DA2=DE•DC=8,
∵DA>0,
∴DA=2,
∵OA2+OD2=2OA2=DA2=8,OA>0,
∴OA=2,
即⊙O的半径为2.
一十.直线与圆的位置关系(共1小题)
11.(2023•扬州)如图,在△ABC中,∠ACB=90°,点D是AB上一点,且∠BCD=∠A,点O在BC上,以点O为圆心的圆经过C、D两点.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若sinB=,⊙O的半径为3,求AC的长.
【答案】(1)直线AB与⊙O相切,理由见解析;(2)6.
【解答】解:(1)直线AB与⊙O相切,
理由:连接OD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠DOB=∠OCD+∠ODC=2∠BCD,
∴,
∵∠BCD=∠A,
∴∠BOD=∠A,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠BOD+∠B=90°,
∴∠BDO=90°,
∵OD是⊙O的半径,
∴直线AB与⊙O相切;
(2)∵sinB==,OD=3,
∴OB=5,
∴BC=OB+OC=8,
在Rt△ACB中,sinB==,
∴设AC=3x,AB=5x,
∴BC==4x=8,
∴x=2,
∴AC=3x=6.
一十一.命题与定理(共1小题)
12.(2023•泰州)如图,CD是五边形ABCDE的一边,若AM垂直平分CD,垂足为M,且 ② , ③ ,则 ① .
给出下列信息:①AM平分∠BAE;②AB=AE;③BC=DE.请从中选择适当信息,将对应的序号填到横线上方,使之构成真命题,补全图形,并加以证明.
【答案】②③①或①②③证明详见解析.(答案不唯一)
【解答】证明:根据题意补全图形并连接AC、AD,如图所示:
(1)且②③则①:
∵AM垂直平分CD,
∴CM=DM,AC=AD(线段垂直平分线上的点到线段两个端点的距离相等),
在△ACM与△ADM中,
,
∴△ACM≌△ADM(SSS),
∴∠CAM=∠DAM,
在△ABC与△AED中,
,
∴△ABC≌△AED(SSS),
∴∠BAC=∠EAD,
又∵∠CAM=∠DAM,
∴∠BAC+∠CAM=∠EAD+∠DAM,
即∠BAM=∠EAM=∠BAE,
∴AM平分∠BAE.
(2)且①②则③:
∵AM垂直平分CD,
∴CM=DM,AC=AD(线段垂直平分线上的点到线段两个端点的距离相等),
在△ACM与△ADM中,
,
∴△ACM≌△ADM(SSS),
∴∠CAM=∠DAM,
∵AM平分∠BAE,
∴∠BAM=∠EAM,
又∵∠CAM=∠DAM,
∴∠BAM﹣∠CAM=∠EAM﹣∠DAM,
即∠BAC=∠EAD,
在△ABC与△AED中,
∴△ABC≌△AED(SAS),
∴BC=DE.
故答案为:②③①或①②③.
一十二.用样本估计总体(共1小题)
13.(2023•泰州)如图是我国2019~2022年汽车销售情况统计图.
根据图中信息,解答下列问题:
(1)2022年我国新能源汽车销售量约占该年各类汽车销售总量的 26 %(精确到1%);这4年中,我国新能源汽车销售量在各类汽车销售总量占比最高的年份是 2022 年;
(2)小明说:新能源汽车2022年的销售量超过前3年的总和,所以2022年新能源汽车销售量的增长率比2021年高.你同意他的说法吗?请结合统计图说明你的理由.
【答案】(1)26,2022年;
(2)不同意.理由见解析.
【解答】解:(1)2022年我国新能源汽车销售量约占该年各类汽车销售总量的占比为:×100%≈26%,
2021年我国新能源汽车销售量约占该年各类汽车销售总量的占比为:×100%≈13%,
2020年我国新能源汽车销售量约占该年各类汽车销售总量的占比为:×100%≈5%,
2019年我国新能源汽车销售量约占该年各类汽车销售总量的占比为:×100%≈5%,
∴这4年中,我国新能源汽车销售量在各类汽车销售总量占比最高的年份是2022年.
故答案为:26,2022年;
(2)不同意.理由如下:
2022年新能源汽车销售量的增长率为:×100%≈96%,
2021年新能源汽车销售量的增长率为:×100%≈157%,
∴2022年新能源汽车销售量的增长率比2021年低.
一十三.条形统计图(共1小题)
14.(2023•苏州)某初中学校为加强劳动教育,开设了劳动技能培训课程.为了解培训效果,学校对七年级320名学生在培训前和培训后各进行一次劳动技能检测,两次检测项目相同,评委依据同一标准进行现场评估,分成“合格”、“良好”、“优秀”3个等级,依次记为2分、6分、8分(比如,某同学检测等级为“优秀”,即得8分).学校随机抽取32名学生的2次检测等级作为样本,绘制成如图的条形统计图:
(1)这32名学生在培训前得分的中位数对应等级应为 合格 ;(填“合格”、“良好”或“优秀”)
(2)求这32名学生培训后比培训前的平均分提高了多少?
(3)利用样本估计该校七年级学生中,培训后检测等级为“良好”与“优秀”的学生人数之和是多少?
【答案】(1)合格;
(2)提高2.5分;
(3)240名.
【解答】解:(1)由题意得,这32名学生在培训前得分的中位数对应等级应为合格,
故答案为:合格;
(2)培训前的平均分为:(25×2+5×6+2×8)÷32=3(分),
培调后的平均分为:(8×2+16×6+8×8)÷32=5.5(分),
培训后比培训前的平均分提高2.5分;
(3)解法示例:
样本中培训后“良好”的比例为:=0.50,
样本中培训后“优秀”的比例为:==0.25,
∴培训后考分等级为“良好”与“优秀”的学生共有320×75%=240(名).
一十四.列表法与树状图法(共2小题)
15.(2023•泰州)某校组织学生去敬老院表演节目,表演形式有舞蹈、情景剧和唱歌3种类型.小明、小丽2人积极报名参加,从3种类型中随机挑选一种类型.求小明、小丽选择不同类型的概率.
【答案】.
【解答】解:用树状图法表示所有等可能出现的结果如下:
共有9种等可能出现的结果,其中小明、小丽选择不同类型的有6种,
所以小明、小丽选择不同类型的概率为.
16.(2023•扬州)扬州是个好地方,有着丰富的旅游资源.某天甲、乙两人来扬州旅游,两人分别从A、B、C三个景点中随机选择一个景点游览.
(1)甲选择A景点的概率为 ;
(2)请用画树状图或列表的方法,求甲、乙两人中至少有一人选择C景点的概率.
【答案】(1);
(2)甲、乙两人中至少有一人选择C景点的概率是.
【解答】解:(1)甲选择A景点的概率为,
故答案为:;
(2)根据题意画树状图如下:
∵共有9种等可能的情况,其中甲、乙两人中至少有一人选择C景点的情况有5种,
∴甲、乙两人中至少有一人选择C景点的概率是.
湖北省各地市2023中考数学真题分类汇编03解答题(基础题)知识点分类①: 这是一份湖北省各地市2023中考数学真题分类汇编03解答题(基础题)知识点分类①,共15页。试卷主要包含了化简;,先化简,再求值,,其中x=﹣2,x+m2+m=0,解不等式组请按下列步骤完成解答等内容,欢迎下载使用。
湖北省各地市2023中考数学真题分类汇编03解答题(基础题)知识点分类②: 这是一份湖北省各地市2023中考数学真题分类汇编03解答题(基础题)知识点分类②,共15页。试卷主要包含了先化简,再求值,创建文明城市,构建美好家园,与函数为的图象交于两点等内容,欢迎下载使用。
湖北省各地市2023中考数学真题分类汇编03解答题(提升题)知识点分类①: 这是一份湖北省各地市2023中考数学真题分类汇编03解答题(提升题)知识点分类①,共23页。












