辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类

这是一份辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类，共23页。试卷主要包含了，其中x＝4，，其中m＝2，，与x轴交于点C等内容，欢迎下载使用。
辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类
一．分式的化简求值（共2小题）
1．（2023•鞍山）先化简，再求值：（+1），其中x＝4．
2．（2022•鞍山）先化简，再求值：÷（1﹣），其中m＝2．
二．反比例函数与一次函数的交点问题（共3小题）
3．（2023•鞍山）如图，直线AB与反比例函数的图象交于点A（﹣2，m），B（n，2），过点A作AC∥y轴交x轴于点C，在x轴正半轴上取一点D，使OC＝2OD，连接BC，AD，若△ACD的面积是6．
（1）求反比例函数的解析式．
（2）点P为第一象限内直线AB上一点，且△PAC的面积等于△BAC面积的2倍，求点P的坐标．

4．（2022•鞍山）如图，在平面直角坐标系中，一次函数y＝x+2的图象与反比例函数y＝（x＞0）的图象交于点A（1，m），与x轴交于点C．
（1）求点A的坐标和反比例函数的解析式；
（2）点B是反比例函数图象上一点且纵坐标是1，连接AB，CB，求△ACB的面积．

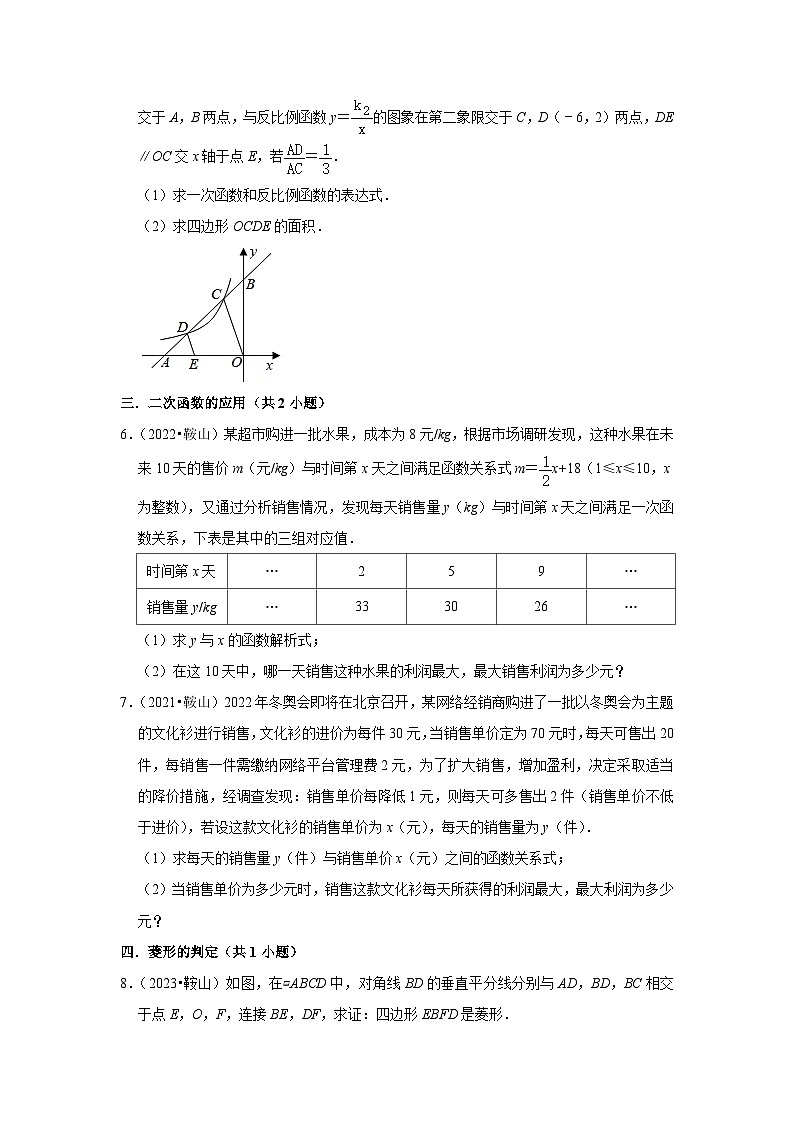
5．（2021•鞍山）如图，在平面直角坐标系中，一次函数y＝k1x+b的图象分别与x轴、y轴交于A，B两点，与反比例函数y＝的图象在第二象限交于C，D（﹣6，2）两点，DE∥OC交x轴于点E，若＝．
（1）求一次函数和反比例函数的表达式．
（2）求四边形OCDE的面积．

三．二次函数的应用（共2小题）
6．（2022•鞍山）某超市购进一批水果，成本为8元/kg，根据市场调研发现，这种水果在未来10天的售价m（元/kg）与时间第x天之间满足函数关系式m＝x+18（1≤x≤10，x为整数），又通过分析销售情况，发现每天销售量y（kg）与时间第x天之间满足一次函数关系，下表是其中的三组对应值．
时间第x天
…
2
5
9
…
销售量y/kg
…
33
30
26
…
（1）求y与x的函数解析式；
（2）在这10天中，哪一天销售这种水果的利润最大，最大销售利润为多少元？
7．（2021•鞍山）2022年冬奥会即将在北京召开，某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件，每销售一件需缴纳网络平台管理费2元，为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），每天的销售量为y（件）．
（1）求每天的销售量y（件）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，销售这款文化衫每天所获得的利润最大，最大利润为多少元？
四．菱形的判定（共1小题）
8．（2023•鞍山）如图，在▱ABCD中，对角线BD的垂直平分线分别与AD，BD，BC相交于点E，O，F，连接BE，DF，求证：四边形EBFD是菱形．

五．切线的判定与性质（共1小题）
9．（2022•鞍山）如图，⊙O是△ABC的外接圆，AB为⊙O的直径，点E为⊙O上一点，EF∥AC交AB的延长线于点F，CE与AB交于点D，连接BE，若∠BCE＝∠ABC．
（1）求证：EF是⊙O的切线．
（2）若BF＝2，sin∠BEC＝，求⊙O的半径．

六．相似三角形的判定与性质（共1小题）
10．（2021•鞍山）如图，AB为⊙O的直径，C为⊙O上一点，D为AB上一点，BD＝BC，过点A作AE⊥AB交CD的延长线于点E，CE交⊙O于点G，连接AC，AG，在EA的延长线上取点F，使∠FCA＝2∠E．
（1）求证：CF是⊙O的切线；
（2）若AC＝6，AG＝，求⊙O的半径．

七．条形统计图（共3小题）
11．（2023•鞍山）在第六十个学雷锋纪念日到来之际，习近平总书记指出：实践证明，无论时代如何变迁，雷锋精神永不过时，某校为弘扬雷锋精神，组织全校学生开展了手抄报评比活动．评比结果共分为四项：A．非凡创意；B．魅力色彩；C，最美设计：D．无限潜力．参赛的每名学生都恰好获得其中一个奖项，活动结束后，学校数学兴趣小组随机调查了部分学生的获奖情况，将调查结果绘制成如下两幅不完整的统计图．

请根据统计图提供的信息，解答下列问题：
（1）本次共调查了 　 　名学生．
（2）请补全条形统计图．
（3）本次评比活动中，全校有800名学生参加，根据调查结果，请你估计在评比中获得“A．非凡创意”奖的学生人数．
12．（2022•鞍山）某校开展“凝心聚力颂家乡”系列活动，组建了四个活动小组供学生参加：A（朗诵），B（绘画），C（唱歌），D（征文）．学校规定：每名学生都必须参加且只能参加其中一个活动小组．学校随机抽取了部分学生，对其参加活动小组情况进行了调查．根据调查结果绘制成如下两幅不完整的统计图（图1和图2）．
请根据统计图提供的信息，解答下列问题：
（1）本次共调查了 　 　名学生，扇形统计图中“C”对应的圆心角度数为 　 　．
（2）请补全条形统计图．
（3）若该校共有2000名学生，根据调查结果，请你估计这所学校参加D活动小组的学生人数．
13．（2021•鞍山）为庆祝建党100周年，某校开展“学党史•颂党恩”的作品征集活动，征集的作品分为四类：征文、书法、剪纸、绘画．学校随机抽取部分学生的作品进行整理，并根据结果绘制成如下两幅不完整的统计图．

请根据以上信息解答下列问题：
（1）所抽取的学生作品的样本容量是多少？
（2）补全条形统计图．
（3）本次活动共征集作品1200件，估计绘画作品有多少件．
八．列表法与树状图法（共2小题）
14．（2022•鞍山）2022年4月15日是第七个全民国家安全教育日，某校七、八年级举行了一次国家安全知识竞赛，经过评比后，七年级的两名学生（用A，B表示）和八年级的两名学生（用C，D表示）获得优秀奖．
（1）从获得优秀奖的学生中随机抽取一名分享经验，恰好抽到七年级学生的概率是 　 　．
（2）从获得优秀奖的学生中随机抽取两名分享经验，请用列表法或画树状图法，求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率．
15．（2021•鞍山）为了加快推进我国全民新冠病毒疫苗接种，在全国范围内构筑最大免疫屏障，各级政府积极开展接种新冠病毒疫苗的宣传工作．某社区印刷了多套宣传海报，每套海报四张，海报内容分别是：
A．防疫道路千万条，接种疫苗第一条；
B．疫苗接种保安全，战胜新冠靠全员；
C．接种疫苗别再拖，安全保障好处多；
D．疫苗接种连万家，平安健康乐全家．
志愿者小张和小李利用休息时间到某小区张贴海报．
（1）小张从一套海报中随机抽取一张，抽到B海报的概率是 　 　．
（2）小张和小李从同一套海报中各随机抽取一张，用列表法或画树状图法，求他们两个人中有一个人抽到D海报的概率．

辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（基础题）知识点分类
参考答案与试题解析
一．分式的化简求值（共2小题）
1．（2023•鞍山）先化简，再求值：（+1），其中x＝4．
【答案】，原式＝．
【解答】解：（+1）
＝•
＝•
＝，
当x＝4时，原式＝＝．
2．（2022•鞍山）先化简，再求值：÷（1﹣），其中m＝2．
【答案】，﹣．
【解答】解：÷（1﹣）
＝÷
＝
＝，
当m＝2时，原式＝＝﹣．
二．反比例函数与一次函数的交点问题（共3小题）
3．（2023•鞍山）如图，直线AB与反比例函数的图象交于点A（﹣2，m），B（n，2），过点A作AC∥y轴交x轴于点C，在x轴正半轴上取一点D，使OC＝2OD，连接BC，AD，若△ACD的面积是6．
（1）求反比例函数的解析式．
（2）点P为第一象限内直线AB上一点，且△PAC的面积等于△BAC面积的2倍，求点P的坐标．

【答案】（1）y＝﹣．（2）P（2，8）．
【解答】解：（1）∵OC＝2OD，△ACD的面积是6，
∴S△AOC＝4，
∴|k|＝8．
∵图象在第二象限，
∴k＝﹣8，
∴反比例函数解析式为：y＝﹣．
（2）∵点A（﹣2，m），B（n，2）在y＝﹣的图象上，
∴A（﹣2，4），B（﹣4，2），
设直线AB的解析式为y＝kx+b，
，解得，
∴直线AB的解析式为y＝x+6，
∵AC∥y轴交x轴于点C，
∴C（﹣2，0），
∴S△ABC＝×4×2＝4．
设直线AB上在第一象限的点P（m．m+6），
∴S△PAC＝×4×（m+2）＝2S△ABC＝8，
∴2m+4＝8，
∴m＝2，
∴P（2，8）．
4．（2022•鞍山）如图，在平面直角坐标系中，一次函数y＝x+2的图象与反比例函数y＝（x＞0）的图象交于点A（1，m），与x轴交于点C．
（1）求点A的坐标和反比例函数的解析式；
（2）点B是反比例函数图象上一点且纵坐标是1，连接AB，CB，求△ACB的面积．

【答案】（1）A（1，3），反比例函数的解析式为y＝；
（2）6．
【解答】解：（1）∵一次函数y＝x+2的图象过点A（1，m），
∴m＝1+2＝3，
∴A（1，3），
∵点A在反比例函数y＝（x＞0）的图象上，
∴k＝1×3＝3，
∴反比例函数的解析式为y＝；
（2）∵点B是反比例函数图象上一点且纵坐标是1，
∴B（3，1），
作BD∥x轴，交直线AC于点D，则D点的纵坐标为1，
代入y＝x+2得，1＝x+2，解得x＝﹣1，
∴D（﹣1，1），
∴BD＝3+1＝4，
∴S△ABC＝×4×3＝6．

5．（2021•鞍山）如图，在平面直角坐标系中，一次函数y＝k1x+b的图象分别与x轴、y轴交于A，B两点，与反比例函数y＝的图象在第二象限交于C，D（﹣6，2）两点，DE∥OC交x轴于点E，若＝．
（1）求一次函数和反比例函数的表达式．
（2）求四边形OCDE的面积．

【答案】（1）一次函数的解析式为y＝x+8；反比例函数的解析式为y＝﹣；（2）．
【解答】解：（1）将D（﹣6，2）代入y＝中，
k2＝﹣6×2＝﹣12，
∴反比例函数的解析式为y＝﹣；
过点D作DM⊥x轴，过点C作CN⊥x轴，

∵DE∥OC，
∴△ADE∽△ACO，
∴，
∴CN＝3DM＝6，
将y＝6代入y＝﹣中，
﹣，
解得：x＝﹣2，
∴C点坐标为（﹣2，6），
将C（﹣2，6），D（﹣6，2）代入y＝k1x+b中，
可得，
解得：，
∴一次函数的解析式为y＝x+8；
（2）解法一：设直线OC的解析式为y＝mx，
将C（﹣2，6）代入，得：﹣2m＝6，
解得：m＝﹣3，
∴直线OC的解析式为y＝﹣3x，
由DE∥OC，设直线DE的解析式为y＝﹣3x+n，
将D（﹣6，2）代入可得：﹣3×（﹣6）+n＝2，
解得：n＝﹣16，
∴直线DE的解析式为y＝﹣3x﹣16，
当y＝0时，﹣3x﹣16＝0，
解得：x＝﹣，
∴E点坐标为（﹣，0），
∴OE＝，
在y＝x+8中，当y＝0时，x+8＝0，
解得：x＝﹣8，
∴A点坐标为（﹣8，0），
∴OA＝8，
∴AE＝8﹣＝，
S四边形OCDE＝S△AOC﹣S△AED
＝
＝
＝24﹣
＝．
解法二：在y＝x+8中，当y＝0时，x＝﹣8，
∴A点坐标为（﹣8，0），
又∵DE∥OC，
∴△ADE∽△ACO，
∴，
∴AE＝，
∴S四边形OCDE＝S△AOC﹣S△AED
＝
＝
＝24﹣
＝．
三．二次函数的应用（共2小题）
6．（2022•鞍山）某超市购进一批水果，成本为8元/kg，根据市场调研发现，这种水果在未来10天的售价m（元/kg）与时间第x天之间满足函数关系式m＝x+18（1≤x≤10，x为整数），又通过分析销售情况，发现每天销售量y（kg）与时间第x天之间满足一次函数关系，下表是其中的三组对应值．
时间第x天
…
2
5
9
…
销售量y/kg
…
33
30
26
…
（1）求y与x的函数解析式；
（2）在这10天中，哪一天销售这种水果的利润最大，最大销售利润为多少元？
【答案】（1）y＝﹣x+35（1≤x≤10，x为整数）；
（2）在这10天中，第7天和第8天销售这种水果的利润最大，最大销售利润为378元．
【解答】解：（1）设每天销售量y与时间第x天之间满足的一次函数关系式为y＝kx+b，
根据题意，得：，
解得，
∴y＝﹣x+35（1≤x≤10，x为整数）；
（2）设销售这种水果的日利润为w元，
则w＝（﹣x+35）（x+18﹣8）
＝﹣x2+x+350
＝﹣（x﹣）2+，
∵1≤x≤10，x为整数，
∴当x＝7或x＝8时，w取得最大值，最大值为378，
答：在这10天中，第7天和第8天销售这种水果的利润最大，最大销售利润为378元．
7．（2021•鞍山）2022年冬奥会即将在北京召开，某网络经销商购进了一批以冬奥会为主题的文化衫进行销售，文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件，每销售一件需缴纳网络平台管理费2元，为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），每天的销售量为y（件）．
（1）求每天的销售量y（件）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，销售这款文化衫每天所获得的利润最大，最大利润为多少元？
【答案】见试题解答内容
【解答】解：（1）由题意可得：y＝20+2（70﹣x），
整理，得：y＝﹣2x+160，
∴每天的销售量y（件）与销售单价x（元）之间的函数关系式为y＝﹣2x+160（30≤x＜70）；
（2）设销售所得利润为w，由题意可得：
w＝（x﹣30﹣2）y＝（x﹣32）（﹣2x+160）＝﹣2x2+224x﹣5120，
整理，得：w＝﹣2（x﹣56）2+1152，
∵﹣2＜0，
∴当x＝56时，w取最大值为1152，
∴当销售单价为56元时，销售这款文化衫每天所获得的利润最大，最大利润为1152元．
四．菱形的判定（共1小题）
8．（2023•鞍山）如图，在▱ABCD中，对角线BD的垂直平分线分别与AD，BD，BC相交于点E，O，F，连接BE，DF，求证：四边形EBFD是菱形．

【答案】见解析．
【解答】证明：∵∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∴∠EDO＝∠OBF，
∵O是BD中点，
∴BO＝DO，
∵∠EOD＝∠BOF，
在△DEO和△BFO中，
，
∴△DEO≌△BFO（ASA），
∴OE＝OF，
∴四边形EBFD是平行四边形，
又∵EF⊥BD，
∴四边形EBFD是菱形．
五．切线的判定与性质（共1小题）
9．（2022•鞍山）如图，⊙O是△ABC的外接圆，AB为⊙O的直径，点E为⊙O上一点，EF∥AC交AB的延长线于点F，CE与AB交于点D，连接BE，若∠BCE＝∠ABC．
（1）求证：EF是⊙O的切线．
（2）若BF＝2，sin∠BEC＝，求⊙O的半径．

【答案】（1）见解答过程；
（2）⊙O的半径为3．
【解答】（1）证明：连接OE，
∵∠BCE＝∠ABC，∠BCE＝∠BOE，
∴∠ABC＝∠BOE，
∴OE∥BC，
∴∠OED＝∠BCD，
∵EF∥AC，
∴∠FEC＝∠ACE，
∴∠OED+∠FEC＝∠BCD+∠ACE，
即∠FEO＝∠ACB，
∵AB是直径，
∴∠ACB＝90°，
∴∠FEO＝90°，
∴FE⊥EO，
∵EO是⊙O的半径，
∴EF是⊙O的切线．
（2）解：∵EF∥AC，
∴△FEO∽△ACB，
∴，
∵BF＝2，sin∠BEC＝，
设⊙O的半径为r，
∴FO＝2+r，AB＝2r，BC＝r，
∴，
解得：r＝3，
检验得：r＝3是原分式方程的解，
∴⊙O的半径为3．

六．相似三角形的判定与性质（共1小题）
10．（2021•鞍山）如图，AB为⊙O的直径，C为⊙O上一点，D为AB上一点，BD＝BC，过点A作AE⊥AB交CD的延长线于点E，CE交⊙O于点G，连接AC，AG，在EA的延长线上取点F，使∠FCA＝2∠E．
（1）求证：CF是⊙O的切线；
（2）若AC＝6，AG＝，求⊙O的半径．

【答案】（1）见解答过程；（2）5．
【解答】解：（1）∵∠B＝∠AGC，∠ADG＝∠CDB，
∴△ADG∽△DCB，
∴，
∵BD＝BC，
∴GD＝GA，
∴∠ADG＝∠DAG，
又∵AE⊥AB，
∴∠EAD＝90°，
∴∠GAE+∠DAG＝∠E+∠ADG＝90°，
∴∠GAE＝∠E，
∴AG＝DG＝EG，∠AGD＝2∠E，
∵∠FCA＝2∠E，
∴∠FCA＝∠AGD＝∠B，
∵AB是⊙O的直径，
∴∠CAB+∠B＝90°，
又∵OA＝OC，
∴∠ACO＝∠CAB，
∴∠FCA+∠ACO＝90°，
∴∠FCO＝90°，
即CF是⊙O的切线；
（2）∵CF是⊙O的切线，AE⊥AB，
∴AF＝CF，
∴∠FAC＝∠FCA＝2∠E，
∴AC＝AE＝6，
又∵AG＝DG＝EG＝，
在Rt△ADE中，AD＝，
设⊙O的半径为x，则AB＝2x，BD＝BC＝2x﹣2，
在Rt△ABC中，62+（2x﹣2）2＝（2x）2，
解得：x＝5，
∴⊙O的半径为5．
七．条形统计图（共3小题）
11．（2023•鞍山）在第六十个学雷锋纪念日到来之际，习近平总书记指出：实践证明，无论时代如何变迁，雷锋精神永不过时，某校为弘扬雷锋精神，组织全校学生开展了手抄报评比活动．评比结果共分为四项：A．非凡创意；B．魅力色彩；C，最美设计：D．无限潜力．参赛的每名学生都恰好获得其中一个奖项，活动结束后，学校数学兴趣小组随机调查了部分学生的获奖情况，将调查结果绘制成如下两幅不完整的统计图．

请根据统计图提供的信息，解答下列问题：
（1）本次共调查了 　100　名学生．
（2）请补全条形统计图．
（3）本次评比活动中，全校有800名学生参加，根据调查结果，请你估计在评比中获得“A．非凡创意”奖的学生人数．
【答案】（1）100；
（2）详见解答；
（3）64人．
【解答】解：（1）20÷20%＝100（名），
故答案为：100；
（2）样本中获得“B．魅力色彩”的人数为：100﹣8﹣48﹣20＝24（名），
补全条形统计图如下：

（3）800×＝64（人），
答：全校有800名学生中获得“A．非凡创意”奖的学生大约有64人．
12．（2022•鞍山）某校开展“凝心聚力颂家乡”系列活动，组建了四个活动小组供学生参加：A（朗诵），B（绘画），C（唱歌），D（征文）．学校规定：每名学生都必须参加且只能参加其中一个活动小组．学校随机抽取了部分学生，对其参加活动小组情况进行了调查．根据调查结果绘制成如下两幅不完整的统计图（图1和图2）．
请根据统计图提供的信息，解答下列问题：
（1）本次共调查了 　100　名学生，扇形统计图中“C”对应的圆心角度数为 　126°　．
（2）请补全条形统计图．
（3）若该校共有2000名学生，根据调查结果，请你估计这所学校参加D活动小组的学生人数．
【答案】（1）100；126°；
（2）见解答；
（3）320名．
【解答】解：（1）这次学校抽查的学生人数是24÷24%＝100（名），
扇形统计图中“C”对应的圆心角度数为×360°＝126°．
故答案为：100；126°；
（2）B人数为：100﹣（24+35+16）＝25（名），
补全条形图如下：

（3）2000×＝320（名），
答：估计这所学校参加D活动小组的学生人数有320名．
13．（2021•鞍山）为庆祝建党100周年，某校开展“学党史•颂党恩”的作品征集活动，征集的作品分为四类：征文、书法、剪纸、绘画．学校随机抽取部分学生的作品进行整理，并根据结果绘制成如下两幅不完整的统计图．

请根据以上信息解答下列问题：
（1）所抽取的学生作品的样本容量是多少？
（2）补全条形统计图．
（3）本次活动共征集作品1200件，估计绘画作品有多少件．
【答案】（1）120；
（2）36；补全图形见解答过程．
（3）360．
【解答】解：（1）根据题意得：12÷10%＝120（件），
所抽取的学生作品的样本容量是120；
（2）绘画作品为120﹣（42+30+12）＝36（件），
补全统计图，如图所示：

故答案为：36；
（3）根据题意得：1200×＝360（件），
则绘画作品约有360件．
答：本次活动共征集作品1200件时，绘画作品约有360件．
八．列表法与树状图法（共2小题）
14．（2022•鞍山）2022年4月15日是第七个全民国家安全教育日，某校七、八年级举行了一次国家安全知识竞赛，经过评比后，七年级的两名学生（用A，B表示）和八年级的两名学生（用C，D表示）获得优秀奖．
（1）从获得优秀奖的学生中随机抽取一名分享经验，恰好抽到七年级学生的概率是 　　．
（2）从获得优秀奖的学生中随机抽取两名分享经验，请用列表法或画树状图法，求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率．
【答案】（1）；
（2）．
【解答】解：（1）从获得优秀奖的学生中随机抽取一名分享经验，恰好抽到七年级学生的概率是＝，
故答案为：；
（2）列表如下：

A
B
C
D
A

（B，A）
（C，A）
（D，A）
B
（A，B）

（C，B）
（D，B）
C
（A，C）
（B，C）

（D，C）
D
（A，D）
（B，D）
（C，D）

由表知，共有12种等可能结果，其中抽取的两名学生恰好一名来自七年级、一名来自八年级的有8种结果，
所以抽取的两名学生恰好一名来自七年级、一名来自八年级的概率为＝．
15．（2021•鞍山）为了加快推进我国全民新冠病毒疫苗接种，在全国范围内构筑最大免疫屏障，各级政府积极开展接种新冠病毒疫苗的宣传工作．某社区印刷了多套宣传海报，每套海报四张，海报内容分别是：
A．防疫道路千万条，接种疫苗第一条；
B．疫苗接种保安全，战胜新冠靠全员；
C．接种疫苗别再拖，安全保障好处多；
D．疫苗接种连万家，平安健康乐全家．
志愿者小张和小李利用休息时间到某小区张贴海报．
（1）小张从一套海报中随机抽取一张，抽到B海报的概率是 　　．
（2）小张和小李从同一套海报中各随机抽取一张，用列表法或画树状图法，求他们两个人中有一个人抽到D海报的概率．
【答案】（1）；
（2）．
【解答】解：（1）小张从一套海报中随机抽取一张，抽到B海报的概率是，
故答案为：；
（2）画树状图如图：

共有12种等可能的结果，小张和小李两个人中有一个人抽到D海报的结果有6种，
∴小张和小李两个人中有一个人抽到D海报的概率为＝．