辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类

这是一份辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类，共42页。试卷主要包含了÷，其中a＝+2，之间满足如图所示的一次函数关系，，连接BC，，AE∥PD交直线l等内容，欢迎下载使用。

辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
一．分式的化简求值（共1小题）
1．（2021•鞍山）先化简，再求值：（﹣）÷，其中a＝+2．
二．二次函数的应用（共1小题）
2．（2023•鞍山）网络销售已经成为一种热门的销售方式，某果园在网络平台上直播销售荔枝．已知该荔枝的成本为6元/kg，销售价格不高于18元/kg，且每售卖1kg需向网络平台支付2元的相关费用，经过一段时间的直播销售发现，每日销售量y（kg）与销售价格x（元/kg）之间满足如图所示的一次函数关系．
（1）求y与x的函数解析式．
（2）当每千克荔枝的销售价格定为多少元时，销售这种荔枝日获利最大，最大利润为多少元？

三．二次函数综合题（共3小题）
3．（2023•鞍山）如图1，抛物线y＝ax2+x+c经过点（3，1），与y轴交于点B（0，5），点E为第一象限内抛物线上一动点．
（1）求抛物线的解析式．
（2）直线y＝x﹣4与x轴交于点A，与y轴交于点D，过点E作直线EF⊥x轴，交AD于点F，连接BE，当BE＝DF时，求点E的横坐标．
（3）如图2，点N为x轴正半轴上一点，OE与BN交于点M，若OE＝BN，tan∠BME＝，求点E的坐标．

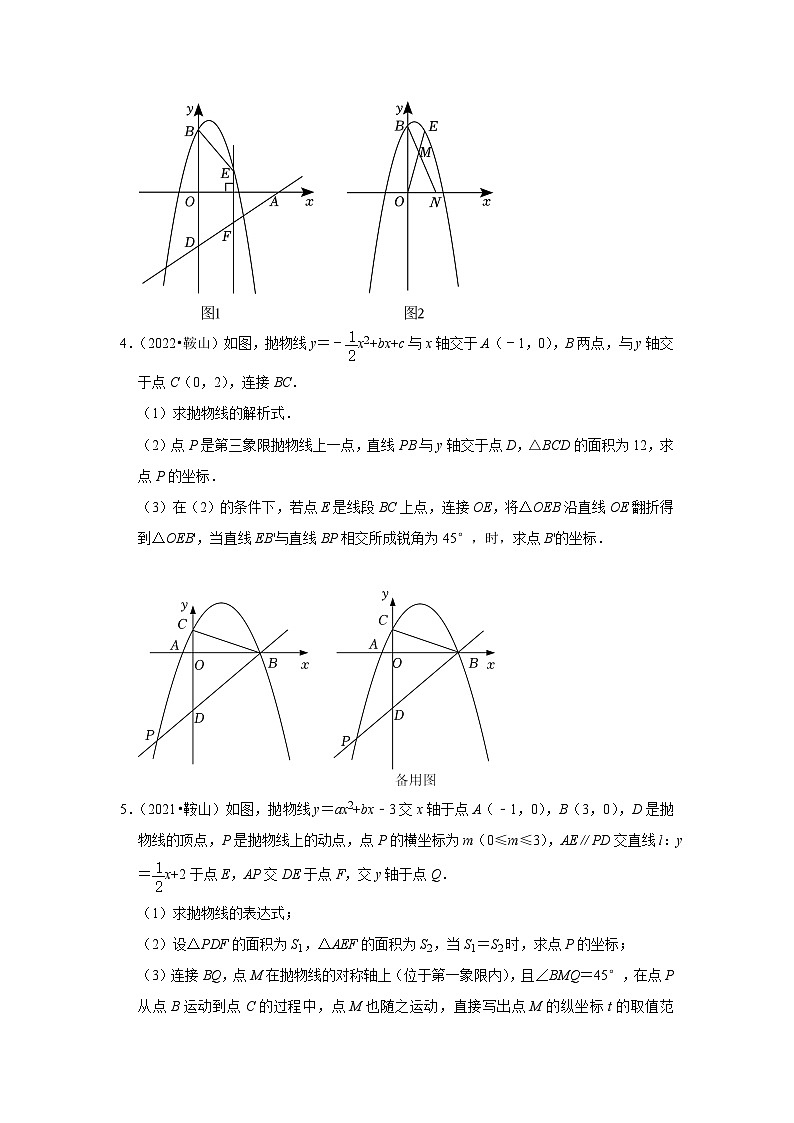
4．（2022•鞍山）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B两点，与y轴交于点C（0，2），连接BC．
（1）求抛物线的解析式．
（2）点P是第三象限抛物线上一点，直线PB与y轴交于点D，△BCD的面积为12，求点P的坐标．
（3）在（2）的条件下，若点E是线段BC上点，连接OE，将△OEB沿直线OE翻折得到△OEB'，当直线EB'与直线BP相交所成锐角为45°，时，求点B'的坐标．


5．（2021•鞍山）如图，抛物线y＝ax2+bx﹣3交x轴于点A（﹣1，0），B（3，0），D是抛物线的顶点，P是抛物线上的动点，点P的横坐标为m（0≤m≤3），AE∥PD交直线l：y＝x+2于点E，AP交DE于点F，交y轴于点Q．
（1）求抛物线的表达式；
（2）设△PDF的面积为S1，△AEF的面积为S2，当S1＝S2时，求点P的坐标；
（3）连接BQ，点M在抛物线的对称轴上（位于第一象限内），且∠BMQ＝45°，在点P从点B运动到点C的过程中，点M也随之运动，直接写出点M的纵坐标t的取值范围．

四．平行四边形的判定（共1小题）
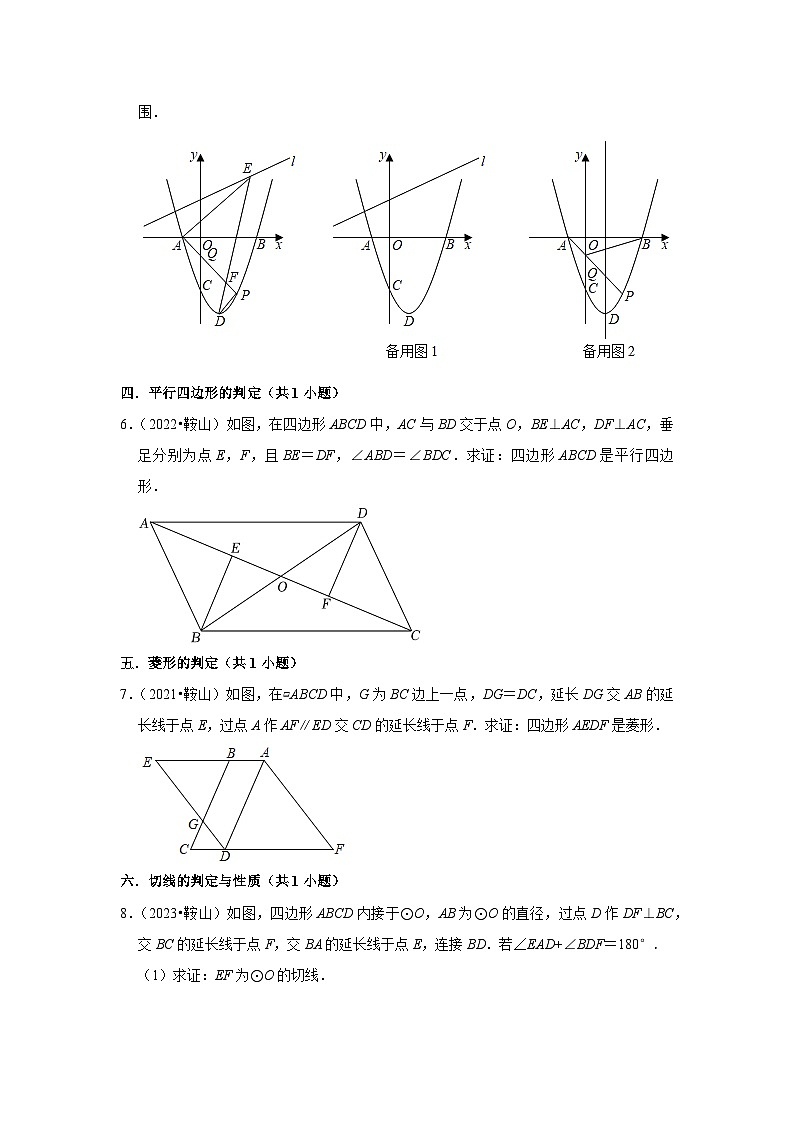
6．（2022•鞍山）如图，在四边形ABCD中，AC与BD交于点O，BE⊥AC，DF⊥AC，垂足分别为点E，F，且BE＝DF，∠ABD＝∠BDC．求证：四边形ABCD是平行四边形．

五．菱形的判定（共1小题）
7．（2021•鞍山）如图，在▱ABCD中，G为BC边上一点，DG＝DC，延长DG交AB的延长线于点E，过点A作AF∥ED交CD的延长线于点F．求证：四边形AEDF是菱形．

六．切线的判定与性质（共1小题）
8．（2023•鞍山）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点D作DF⊥BC，交BC的延长线于点F，交BA的延长线于点E，连接BD．若∠EAD+∠BDF＝180°．
（1）求证：EF为⊙O的切线．
（2）若BE＝10，sin∠BDC＝，求⊙O的半径．

七．几何变换综合题（共2小题）
9．（2022•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝120°，点D在直线AC上，连接BD，将DB绕点D逆时针旋转120°，得到线段DE，连接BE，CE．
（1）求证：BC＝AB；
（2）当点D在线段AC上（点D不与点A，C重合）时，求的值；
（3）过点A作AN∥DE交BD于点N，若AD＝2CD，请直接写出的值．


10．（2021•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α（0°＜α＜180°），过点A作射线AM交射线BC于点D，将AM绕点A逆时针旋转α得到AN，过点C作CF∥AM交直线AN于点F，在AM上取点E，使∠AEB＝∠ACB．
（1）当AM与线段BC相交时，
①如图1，当α＝60°时，线段AE，CE和CF之间的数量关系为 　 　．
②如图2，当α＝90°时，写出线段AE，CE和CF之间的数量关系，并说明理由．
（2）当tanα＝，AB＝5时，若△CDE是直角三角形，直接写出AF的长．

八．相似形综合题（共1小题）
11．（2023•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α，点D是射线BC上的动点（不与点B，C重合），连接AD，过点D在AD左侧作DE⊥AD，使AD＝kDE，连接AE，点F，G分别是AE，BD的中点，连接DF，FG，BE．
（1）如图1，点D在线段BC上，且点D不是BC的中点，当α＝90°，k＝1时，AB与BE的位置关系是 　 　，＝　 　．
（2）如图2，点D在线段BC上，当α＝60°，k＝时，求证：BC+CD＝2FG．
（3）当α＝60°，k＝时，直线CE与直线AB交于点N，若BC＝6，CD＝5，请直接写出线段CN的长．
九．解直角三角形的应用（共1小题）
12．（2023•鞍山）某商店窗前计划安装如图1所示的遮阳棚，其截面图如图2所示，在截面图中，墙面BC垂直于地面CE，遮阳棚与墙面连接处点B距地面高3m，即BC＝3m，遮阳棚AB与窗户所在墙面BC垂直，即∠ABC＝∠BCE＝90°，假设此地正午时太阳光与地面的夹角恰为60°（若经过点A的光线恰好照射在地面点D处，则∠ADE＝60°），为使正午时窗前地面上能有1m宽的阴影区域，即CD＝1m，求遮阳棚的宽度AB．（结果精确到0.1m，参考数据：≈1.73）

一十．解直角三角形的应用-仰角俯角问题（共1小题）
13．（2022•鞍山）北京时间2022年4月16日9时56分，神舟十三号载人飞船返回舱成功着陆．为弘扬航天精神，某校在教学楼上悬挂了一幅长为8m的励志条幅（即GF＝8m）．小亮同学想知道条幅的底端F到地面的距离，他的测量过程如下：如图，首先他站在楼前点B处，在点B正上方点A处测得条幅顶端G的仰角为37°，然后向教学楼条幅方向前行12m到达点D处（楼底部点E与点B，D在一条直线上），在点D正上方点C处测得条幅底端F的仰角为45°，若AB，CD均为1.65m（即四边形ABDC为矩形），请你帮助小亮计算条幅底端F到地面的距离FE的长度．（结果精确到0.1m．参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

一十一．解直角三角形的应用-方向角问题（共1小题）
14．（2021•鞍山）小明和小华约定一同去公园游玩，公园有南北两个门，北门A在南门B的正北方向，小明自公园北门A处出发，沿南偏东30°方向前往游乐场D处；小华自南门B处出发，沿正东方向行走150m到达C处，再沿北偏东22.6°方向前往游乐场D处与小明汇合（如图所示），两人所走的路程相同．求公园北门A与南门B之间的距离．（结果取整数．参考数据：sin22.6°≈，cos22.6°≈，tan22.6°≈，≈1.732）

一十二．列表法与树状图法（共1小题）
15．（2023•鞍山）二十四节气是中国古代一种用来指导农事的补充历法，在国际气象界被誉为“中国的第五大发明”，并位列联合国教科文组织人类非物质文化遗产代表作名录，小明和小亮对二十四节气非常感兴趣，在课间玩游戏时，准备了四张完全相同的不透明卡片，卡片正面分别写有“A．惊蛰”“B．夏至”“C．白露”“D．霜降”四个节气，两人商量将卡片背面朝上洗匀后，从中随机抽取一张，并讲述所抽卡片上的节气的由来与习俗．
（1）小明从四张卡片中随机抽取一张卡片，抽到“A．惊蛰”的概率是 　 　．
（2）小明先从四张卡片中随机抽取一张，小亮再从剩下的卡片中随机抽取一张，请用列表或画树状图的方法，求两人都没有抽到“B．夏至”的概率．

辽宁省鞍山市2021-2023三年中考数学真题分类汇编-03解答题（提升题）知识点分类
参考答案与试题解析
一．分式的化简求值（共1小题）
1．（2021•鞍山）先化简，再求值：（﹣）÷，其中a＝+2．
【答案】1+．
【解答】解：
＝
＝×
＝．
当a＝+2时，原式＝＝＝1+．
二．二次函数的应用（共1小题）
2．（2023•鞍山）网络销售已经成为一种热门的销售方式，某果园在网络平台上直播销售荔枝．已知该荔枝的成本为6元/kg，销售价格不高于18元/kg，且每售卖1kg需向网络平台支付2元的相关费用，经过一段时间的直播销售发现，每日销售量y（kg）与销售价格x（元/kg）之间满足如图所示的一次函数关系．
（1）求y与x的函数解析式．
（2）当每千克荔枝的销售价格定为多少元时，销售这种荔枝日获利最大，最大利润为多少元？

【答案】（1）y与x的函数解析式为y＝﹣100x+3000；
（2）当销售单价定为18时，销售这种荔枝日获利最大，最大利润为12000元．
【解答】解：（1）设每日销售量y（kg）与销售价格x（元/kg）之间满足如图所示的一次函数关系为y＝kx+b，
∴，
解得，
∴y与x的函数解析式为y＝﹣100x+3000；
（2）设每千克荔枝的销售价格定为x元时，销售这种荔枝日获利为w元，
根据题意得，w＝（x﹣6﹣2）（﹣100x+3000）＝﹣100x2+3800x﹣24000＝﹣100（x﹣19）2+12100，
∵a＝﹣100＜0，对称轴为x＝19，
∵销售价格不高于18元/kg，
∴当x＝18时，w有最大值为12000元，
∴当销售单价定为18时，销售这种荔枝日获利最大，最大利润为12000元．
三．二次函数综合题（共3小题）
3．（2023•鞍山）如图1，抛物线y＝ax2+x+c经过点（3，1），与y轴交于点B（0，5），点E为第一象限内抛物线上一动点．
（1）求抛物线的解析式．
（2）直线y＝x﹣4与x轴交于点A，与y轴交于点D，过点E作直线EF⊥x轴，交AD于点F，连接BE，当BE＝DF时，求点E的横坐标．
（3）如图2，点N为x轴正半轴上一点，OE与BN交于点M，若OE＝BN，tan∠BME＝，求点E的坐标．

【答案】（1）；（2）或1；（3）E（）或E（）．
【解答】解：（1）把（3，1）和（0，5）代入到解析式中可得：，
解得，
∴抛物线的解析式为：；
（2）直线y＝x﹣4中，令y＝0可得A（6，0），
直线y＝x﹣4中，令x＝0，可得D（0，﹣4），
①分别过E、F向y轴作垂线，垂足为G、H，根据题意可得EG＝FH，如图：

∵EG⊥y轴，FH⊥y轴，
∴△BEG和△DFH为直角三角形，
在Rt△BEG和Rt△DFH中：
，
∴Rt△BEG≌Rt△DFH（HL），
∴BG＝DH，
设E（），则F（），
∴G（），H（），
从而BG＝，DH＝，
则有，解得t＝0（舍去）或，
②如图：

同理可得﹣t2+t+5﹣5＝t﹣4﹣（﹣4），
解得t＝0（舍去）或t＝1，
故E点的横坐标为：或1；
（3）将OE平移到NP，连接EP，则四边形ONPE为平行四边形，tan∠BNP＝tan∠BME＝，
过P作PQ⊥BN于Q，过Q作QR⊥y轴于R，过P作PS⊥RQ交延长线于S，延长PE交y轴于T，如图：

设BN＝OE＝NP＝5m，则PQ＝3m，QN＝4m，BQ＝m，
∵RQ∥x轴，
∴△BRQ∽△BON，
∴，
∴，
RO＝4，EP＝NO＝5RQ＝5n，
设RQ＝n，
∵PQ⊥BM，PS⊥RS，BR⊥RS，
∴∠BRQ＝∠QSP＝∠BQP＝90°，
∴∠BQR+∠PQS＝90°，
∠BQR+∠QBR＝90°，
∴∠PQS＝∠QBR，
∴△BRQ∽△QSP，
∴，
∴PS＝3n，QS＝3，则RS＝3+n，
∴xE＝TE＝TP﹣EP＝RS﹣EP＝3+n﹣5n＝3﹣4n，
yE＝TO＝TR+RO＝PS+RO＝3n+4，
∴E（3﹣4n，3n+4），代入抛物线解析式中有：
3n+4＝，
解得：或，
当时，E（）；
当时，E（）．
4．（2022•鞍山）如图，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B两点，与y轴交于点C（0，2），连接BC．
（1）求抛物线的解析式．
（2）点P是第三象限抛物线上一点，直线PB与y轴交于点D，△BCD的面积为12，求点P的坐标．
（3）在（2）的条件下，若点E是线段BC上点，连接OE，将△OEB沿直线OE翻折得到△OEB'，当直线EB'与直线BP相交所成锐角为45°，时，求点B'的坐标．


【答案】（1）y＝﹣x2+x+2；
（2）P（﹣3，﹣7）；
（3）（，）或（﹣，）．
【解答】解：（1）将A（﹣1，0），C（0，2）代入y＝﹣x2+bx+c，
∴，
解得，
∴y＝﹣x2+x+2；
（2）令y＝0，则﹣x2+x+2＝0，
解得x＝﹣1或x＝4，
∴B（4，0），
∴OB＝4，
∴S△BCD＝×4×（2+OD）＝12，
∴OD＝4，
∴D（0，﹣4），
设直线BD的解析式为y＝kx+b，
∴，
解得，
∴y＝x﹣4，
联立方程组，
解得或，
∴P（﹣3，﹣7）；
（3）如图1，当B'在第一象限时，
设直线BC的解析式为y＝k'x+b'，
∴，
解得，
∴y＝﹣x+2，
设E（t，﹣t+2），
∴OH＝t，EH＝﹣t+2，
∵D（0，﹣4），B（4，0），
∴OB＝OD，
∴∠ODB＝45°，
∵直线EB'与直线BP相交所成锐角为45°，
∴EB'∥CD，
由折叠可知，OB'＝BO＝4，BE＝B'E，
在Rt△OHB'中，B'H＝，
∴B'E＝﹣（﹣t+2）＝+t﹣2，
∴BE＝+t﹣2，
在Rt△BHE中，（+t﹣2）2＝（4﹣t）2+（﹣t+2）2，
解得t＝，
∵0≤t≤4，
∴t＝，
∴B'（，）；
如图2，当B'在第二象限，∠BGB'＝45°时，
∵∠ABP＝45°，
∴B'G∥x轴，
∵将△OEB沿直线OE翻折得到△OEB'，
∴BE＝B'E，OB＝OB'，∠BOE＝∠B'OE，
∴∠BOE＝∠B'EO，
∴B'E∥B'O，
∵B'E＝BO，
∴四边形 B'OBE是平行四边形，
∴B'E＝4，
∴B'（t﹣4，﹣t+2），
由折叠可知OB＝OB'＝4，
∴平行四边形OBEB'是菱形，
∴BE＝OB，
∴＝4，
解得t＝4+或t＝4﹣，
∵0≤t≤4，
∴t＝4﹣，
∴B'（﹣，）；
综上所述：B'的坐标为（，）或（﹣，）．
方法2：在Rt△BCO中，BC＝2，CO：OB：BC＝1：2：，
∵BP与x轴和y轴的夹角都是45°，BP与B'E的夹角为45°，
∴B'E∥x轴或B'E∥y轴，
当B'E∥y轴时，延长B'E交x轴于F，
∴B'F⊥OB，
∵∠CBA＝∠OB'E，
∴△OB'F∽△CBO，
∴OF：FB'：B'O＝1：2：，
∵OB＝OB'＝4，
∴FO＝，B'F＝，
∴B'（，）；
当B'E∥x轴时，过B'作B'F⊥x中交于F，
∴B'F⊥OF，B'E∥OB，
∵B'E和BE关于OE对称，OB和OB'关于OE对称，
∴BE∥OB'，
∵∠FOB'＝∠OBC，
∴△OB'F∽△BCO，
∴B'F：FO：OB'＝1：2：，
∵OB＝OB'＝4，
∴B'F＝，OF＝，
∴B'（﹣，）；
综上所述：B'坐标为（，）或（﹣，）．




5．（2021•鞍山）如图，抛物线y＝ax2+bx﹣3交x轴于点A（﹣1，0），B（3，0），D是抛物线的顶点，P是抛物线上的动点，点P的横坐标为m（0≤m≤3），AE∥PD交直线l：y＝x+2于点E，AP交DE于点F，交y轴于点Q．
（1）求抛物线的表达式；
（2）设△PDF的面积为S1，△AEF的面积为S2，当S1＝S2时，求点P的坐标；
（3）连接BQ，点M在抛物线的对称轴上（位于第一象限内），且∠BMQ＝45°，在点P从点B运动到点C的过程中，点M也随之运动，直接写出点M的纵坐标t的取值范围．

【答案】（1）抛物线的表达式为：y＝x2﹣2x﹣3；
（2）P（，﹣）或（0，﹣3）；
（3）2≤t≤．
【解答】解：（1）∵抛物线y＝ax2+bx﹣3交x轴于点A（﹣1，0），B（3，0），
∴将A、B坐标分别代入抛物线解析式得：，
解得：，
∴抛物线的表达式为：y＝x2﹣2x﹣3；
（2）如图，∵D是抛物线的顶点，抛物线的表达式为：y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴D（1，﹣4），
∵AE∥PD交直线l：y＝x+2于点E，P是抛物线上的动点，点P的横坐标为m（0≤m≤3），
∴△AEF∽△PDF，设E（e，e+2），P（m，m2﹣2m﹣3），
又∵△PDF的面积为S1，△AEF的面积为S2，S1＝S2，
∴△AEF≌△PDF，
∴AF＝PF，EF＝DF，即点F分别是AP、ED的中点，
又∵A（﹣1，0），P（m，m2﹣2m﹣3），E（e，e+2），D（1，﹣4），
∴由中点坐标公式得：，
解得：m1＝0，m2＝，
∴点P的坐标为（，﹣）或（0，﹣3）；
（3）①当点P与点B重合时，点Q与点O重合，此时t的值最大，如图2，
以OB为斜边在第一象限内作等腰直角△O′OB，
则O′（，），OO′＝O′B＝，
以O′为圆心，OO′为半径作⊙O′，交抛物线对称轴于点M（1，t），
过点O′作O′H⊥y轴于点H，则∠O′HM＝90°，
∵O′H＝﹣1＝，O′M＝OO′＝，
∴MH＝＝＝，
∴t＝+＝，
②当点P与点C重合时，点Q与点C重合，此时t的值最小，如图3，
连接BC，以O为圆心，OB为半径作⊙O交抛物线对称轴于点M，
∵OB＝OC＝3，
∴⊙O经过点C，
连接OM，设抛物线对称轴交x轴于点E，
则OM＝OB＝3，OE＝1，
∵∠MEO＝90°，
∴ME＝＝＝2，
∴t＝2，
综上所述，2≤t≤．



四．平行四边形的判定（共1小题）
6．（2022•鞍山）如图，在四边形ABCD中，AC与BD交于点O，BE⊥AC，DF⊥AC，垂足分别为点E，F，且BE＝DF，∠ABD＝∠BDC．求证：四边形ABCD是平行四边形．

【答案】证明过程见解答部分．
【解答】证明：∵∠ABD＝∠BDC，
∴AB∥CD．
∴∠BAE＝∠DCF．
在△ABE与△CDF中，
．
∴△ABE≌△CDF（AAS）．
∴AB＝CD．
∴四边形ABCD是平行四边形．
五．菱形的判定（共1小题）
7．（2021•鞍山）如图，在▱ABCD中，G为BC边上一点，DG＝DC，延长DG交AB的延长线于点E，过点A作AF∥ED交CD的延长线于点F．求证：四边形AEDF是菱形．

【答案】证明见解析．
【解答】证明：∵四边形ABCD是平行四边形，
∴∠BAD＝∠C，AD∥BC，AB∥CD，
∵AF∥ED，
∴四边形AEDF是平行四边形，
∵AD∥BC，
∴∠DGC＝∠ADE，
∵DG＝DC，
∴∠DGC＝∠C，
∴∠BAD＝∠ADE，
∴AE＝DE，
∴平行四边形AEDF是菱形．
六．切线的判定与性质（共1小题）
8．（2023•鞍山）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点D作DF⊥BC，交BC的延长线于点F，交BA的延长线于点E，连接BD．若∠EAD+∠BDF＝180°．
（1）求证：EF为⊙O的切线．
（2）若BE＝10，sin∠BDC＝，求⊙O的半径．

【答案】（1）见解答；
（2）4．
【解答】（1）证明：连接OD，如图：

∵AB为⊙O的直径，
∴∠ACB＝90°，
∵DF⊥BC，
∴∠F＝90°，
∵∠EAD+∠BDF＝180°．
∴∠BDF＝∠BAD，
∴∠ABD＝∠DBF，
∵OB＝OD，
∴∠ABD＝∠ODB，
∴∠ODB＝∠DBF，
∴OD∥BF，
∵BF⊥EF，
∴OD⊥EF，
∵OD是半径，
∴EF为⊙O的切线．
（2）解：连接AC，如图，

∵AB为⊙O的直径，
∴∠ADB＝90°，
∵DF⊥BC，
∴AC∥EF，
∴∠E＝∠BAC＝∠BDC，
设半径为r，则OE＝10﹣r，
在Rt△EOD中，
sinE＝sin∠BDC＝，即，
解得r＝4，
经检验，r＝4是原方程的解，
∴⊙O的半径为4．
七．几何变换综合题（共2小题）
9．（2022•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝120°，点D在直线AC上，连接BD，将DB绕点D逆时针旋转120°，得到线段DE，连接BE，CE．
（1）求证：BC＝AB；
（2）当点D在线段AC上（点D不与点A，C重合）时，求的值；
（3）过点A作AN∥DE交BD于点N，若AD＝2CD，请直接写出的值．


【答案】（1）证明过程详见解答；
（2）；
（3）或．
【解答】（1）证明：如图1，

作AH⊥BC于H，
∵AB＝AC，
∴∠BAH＝∠CAH＝＝60°，BC＝2BH，
∴sin60°＝，
∴BH＝，
∴BC＝2BH＝；
（2）解：∵AB＝AC，
∴∠ABC＝∠ACB＝＝30°，
由（1）得，
，
同理可得，
∠DBE＝30°，，
∴∠ABC＝∠DBE，＝，
∴∠ABC﹣∠DBC＝∠DBE﹣∠DBC，
∴∠ABD＝∠CBE，
∴△ABD∽△CBE，
∴；
（3）解：如图2，

当点D在线段AC上时，
作BF⊥AC，交CA的延长线于F，作AG⊥BD于G，
设AB＝AC＝3a，则AD＝2a，
由（1）得，CE＝，
在Rt△ABF中，∠BAF＝180°﹣∠BAC＝60°，AB＝3a，
∴AF＝3a•cos60°＝，BF＝3a．sin60°＝，
在Rt△BDF中，DF＝AD+AF＝2a+a＝，
BD＝＝＝a，
∵∠AGD＝∠F＝90°，∠ADG＝∠BDF，
∴△DAG∽△DBF，
∴，
∴＝，
∴AG＝，
∵AN∥DE，
∴∠AND＝∠BDE＝120°，
∴∠ANG＝60°，
∴AN＝＝a＝a，
∴＝，
如图3，

当点D在AC的延长线上时，
设AB＝AC＝2a，则AD＝4a，
由（1）得，
CE＝＝4，
作BR⊥CA，交CA的延长线于R，作AQ⊥BD于Q，
同理可得，
AR＝a，BR＝，
∴BD＝＝2a，
∴，
∴AQ＝，
∴AN＝＝a，
∴＝＝，
综上所述：或．
10．（2021•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α（0°＜α＜180°），过点A作射线AM交射线BC于点D，将AM绕点A逆时针旋转α得到AN，过点C作CF∥AM交直线AN于点F，在AM上取点E，使∠AEB＝∠ACB．
（1）当AM与线段BC相交时，
①如图1，当α＝60°时，线段AE，CE和CF之间的数量关系为 　AE＝CF+CE　．
②如图2，当α＝90°时，写出线段AE，CE和CF之间的数量关系，并说明理由．
（2）当tanα＝，AB＝5时，若△CDE是直角三角形，直接写出AF的长．

【答案】（1）①AE＝CF+CE．
②结论：EC＝（AE﹣CF）．证明见解析部分．
（2）AF的值为或．
【解答】解：（1）①结论：AE＝CF+CE．
理由：如图1中，作CT∥AF交AM于T．

∵AB＝AC，∠BAC＝60°，
∴△ABC是等边三角形，
∴CA＝CB，∠ACB＝60°，
∵AF∥CT，CF∥AT，
∴四边形AFCT是平行四边形，
∴CF＝AT，
∵∠ADC＝∠BDE，∠DEB＝∠ACD，
∴△ACD∽△BED，
∴＝，
∴＝，
∵∠ADB＝∠CDE，
∴△ADB∽△CDE，
∴∠ABD＝∠CED＝60°，
∵CT∥AF，
∴∠CTE＝∠FAE＝60°，
∴△CTE是等边三角形，
∴EC＝ET，
∴AE＝AT+ET＝CF+CE．
故答案为：AE＝CF+CE．

②如图2中，结论：EC＝（AE﹣CF）．
理由：过点C作CQ⊥AE于Q．

∵CF∥AM，
∴∠CFA+∠MAN＝180°，
∵∠MAN＝90°，
∴∠CFA＝∠FAQ＝90°，
∵∠CQA＝90°，
∴四边形AFCQ是矩形，
∴CF＝AQ，
∵∠ADC＝∠BDE，∠DEB＝∠ACD，
∴△ACD∽△BED，
∴＝，
∴＝，
∵∠ADB＝∠CDE，
∴△ADB∽△CDE，
∴∠ABD＝∠CED＝45°，
∵∠CQE＝90°，
∴CE＝EQ，
∴AE﹣CF＝AE﹣AQ＝EQ，
∴EC＝（AE﹣CF）．

（2）如图3﹣1中，当∠CDE＝90°时，过点B作BJ⊥AC于J，过点F作FK⊥AE于K．

在Rt△ABJ中，tan∠BAJ＝＝，AB＝5，
∴AJ＝3，BJ＝4，
∵AC＝AB＝5，
∴CJ＝AC﹣AJ＝5﹣3＝2，
∴BC＝＝＝2，
∵•AC•BJ＝•BC•AD，
∴AD＝＝2，
∴CD＝＝＝，
∵FK⊥AD，
∴∠CDE＝∠FKD＝90°，
∴CD∥FK，
∵CF∥DK，
∴四边形CDKF是平行四边形，
∵∠FKD＝90°，
∴四边形CDKF是矩形，
∴FK＝CD＝，
∵tan∠FAK＝tan∠CAB＝，
∴＝，
∴AK＝，
∴AF＝＝＝．

如图3﹣2中，当∠ECD＝90°时，∠DAB＝90°，

∵CF∥AM，
∴∠AKF＝∠DAB＝90°，
在Rt△ACK中，tan∠CAK＝＝，AC＝5，
∴CK＝4，AK＝3，
∵∠MAN＝∠CAB，
∴∠CAN＝∠DAB＝90°，
∴∠CAB+∠BAF＝90°，∠BAF+∠AFK＝90°，
∴∠AFK＝∠CAB，
∴tan∠AFK＝＝，
∴FK＝，
∴AF＝＝＝．
综上所述，满足条件的AF的值为或．
八．相似形综合题（共1小题）
11．（2023•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α，点D是射线BC上的动点（不与点B，C重合），连接AD，过点D在AD左侧作DE⊥AD，使AD＝kDE，连接AE，点F，G分别是AE，BD的中点，连接DF，FG，BE．
（1）如图1，点D在线段BC上，且点D不是BC的中点，当α＝90°，k＝1时，AB与BE的位置关系是 　垂直　，＝　　．
（2）如图2，点D在线段BC上，当α＝60°，k＝时，求证：BC+CD＝2FG．
（3）当α＝60°，k＝时，直线CE与直线AB交于点N，若BC＝6，CD＝5，请直接写出线段CN的长．
【答案】（1）垂直，；
（2）证明过程详见解答；
（3）CN＝或．
【解答】（1）解：如图1，

连接BF并延长交AC于R，
∵AB＝AC，∠BAC＝90°，
∴∠ABC＝∠C＝45°，
同理可得：∠AED＝45°，
∴∠AED＝∠ABD，
∴A、B、E、D共圆，
∴∠ABE+∠ADE＝180°，
∵∠ADE＝90°，
∴∠ABE＝90°，
∴AB与BE垂直，
∵F是AE的中点，
∴BE＝DF＝AE，
∵G是BD的中点，
∴FG⊥BC，
∵∠ABE+∠BAC＝90°+90°＝180°，
∴BE∥AC，
∴∠EAR＝∠FEB，
∵∠AFR＝∠BFE，AF＝EF，
∴△BEF≌△RAF（ASA），
∴BF＝RF，
∴RB∥FG，FG＝，
∵FG⊥BC，
∴RD⊥BC，
∵∠C＝45°，
∴CD＝RD，
∴FG＝，
故答案为：垂直，；
（2）证明：如图2，

作AQ⊥BC于Q，作EH⊥CB，交CB的延长线于H，连接BF，
∵AB＝AC，∠BAC＝60°，
∴△ABC是等边三角形，
∴∠ABC＝60°，
∵∠ADE＝90°，，
∴∠AED＝60°，
∴∠AED＝∠ABC，
∴点A、E、B、D共圆，
∴∠ABE＝∠ADE＝90°，
∵F是AE的中点，
∴BF＝DF＝AE，
∴FG⊥BC，
∴EH∥FG∥AQ，
∴，
∴HG＝QG，
∴FG是梯形AEHQ的中位线，
∴EH+AQ＝2FG，
∴，
∵∠H＝90°，∠EBH＝180°﹣∠ABE﹣∠ABC＝30°，
∴BH＝EH，
∵HG＝QG，BG＝DG，
∴BH＝DQ，
∴DQ＝EH，
∵∠AQC＝90°，∠C＝60°，
∴CQ＝AQ，
∴DQ+3CQ＝2FG，
∴（DQ+CQ）+2CQ＝2FG，
∴BC+CD＝2FG；
（3）解：如图3，

当点D在BC上时，
作EH⊥CB，交CB的延长线于点H，作AQ⊥BC于Q，作CX⊥EB，交EB的延长线于X，
∵△ABC是等边三角形，
∴∠C＝60°，BQ＝CQ＝BC＝3，
∴DQ＝CD﹣CQ＝2，AQ＝AC＝3，
∵∠ADE＝90°，
∴∠EDH+∠ADQ＝90°，
∵∠H＝∠ADQ＝90°，
∴∠ADQ+∠DAQ＝90°，
∴∠EDH＝∠DAQ，
∴△DHE∽△AQD，
∴＝，
∴EH＝＝，
∴BE＝2EH＝，BH＝EH＝2，
∴CH＝BH+BC＝8，
∴CE＝＝，
在Rt△BCX中，BC＝6，∠BCX＝∠EBH＝30°，
∴BX＝6•cos30°＝3，
∴EX＝EB+BX＝，
∵BN∥CX，
∴，
∴，
∴CN＝，
如图4，

当点D在BC的延长线上时，
作EH⊥CB于H，作AQ⊥BC于Q，作CX⊥EB，交EB的延长线于X，
由上可知：AQ＝3，CQ＝3，△DHE∽△AQD，
∴DQ＝CQ+CD＝8，＝，
∴EH＝DQ＝，
∴BH＝EH＝8，BE＝2EH＝，
∴CH＝BH﹣BC＝2，
∴CE＝＝＝，
∵BX＝BC＝3，
∴EX＝BE﹣BX＝，
∵BN∥CX，
∴，
∴
∴CN＝，
综上所述：CN＝或．
九．解直角三角形的应用（共1小题）
12．（2023•鞍山）某商店窗前计划安装如图1所示的遮阳棚，其截面图如图2所示，在截面图中，墙面BC垂直于地面CE，遮阳棚与墙面连接处点B距地面高3m，即BC＝3m，遮阳棚AB与窗户所在墙面BC垂直，即∠ABC＝∠BCE＝90°，假设此地正午时太阳光与地面的夹角恰为60°（若经过点A的光线恰好照射在地面点D处，则∠ADE＝60°），为使正午时窗前地面上能有1m宽的阴影区域，即CD＝1m，求遮阳棚的宽度AB．（结果精确到0.1m，参考数据：≈1.73）

【答案】遮阳棚的宽度AB约为2.7m．
【解答】解：过点D作DF⊥AB，垂足为F，

∴∠DFB＝∠DFA＝90°，
∵∠ABC＝∠BCE＝90°，
∴四边形ABCD是矩形，
∴BC＝DF＝3m，CD＝BF＝1m，AB∥CE，
∴∠BAD＝∠ADE＝60°，
在Rt△ADF中，AF＝＝＝（m），
∴AB＝AF+BF＝1+≈2.7（m），
∴遮阳棚的宽度AB约为2.7m．
一十．解直角三角形的应用-仰角俯角问题（共1小题）
13．（2022•鞍山）北京时间2022年4月16日9时56分，神舟十三号载人飞船返回舱成功着陆．为弘扬航天精神，某校在教学楼上悬挂了一幅长为8m的励志条幅（即GF＝8m）．小亮同学想知道条幅的底端F到地面的距离，他的测量过程如下：如图，首先他站在楼前点B处，在点B正上方点A处测得条幅顶端G的仰角为37°，然后向教学楼条幅方向前行12m到达点D处（楼底部点E与点B，D在一条直线上），在点D正上方点C处测得条幅底端F的仰角为45°，若AB，CD均为1.65m（即四边形ABDC为矩形），请你帮助小亮计算条幅底端F到地面的距离FE的长度．（结果精确到0.1m．参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

【答案】条幅底端F到地面的距离FE的长度约为5.7米．
【解答】解：设AC与GE相交于点H，

由题意得：
AB＝CD＝HE＝1.65米，AC＝BD＝12米，∠AHG＝90°，
设CH＝x米，
∴AH＝AC+CH＝（12+x）米，
在Rt△CHF中，∠FCH＝45°，
∴FH＝CH•tan45°＝x（米），
∵GF＝8米，
∴GH＝GF+FH＝（8+x）米，
在Rt△AHG中，∠GAH＝37°，
∴tan37°＝＝≈0.75，
解得：x＝4，
经检验：x＝4是原方程的根，
∴FE＝FH+HE＝5.65≈5.7（米），
∴条幅底端F到地面的距离FE的长度约为5.7米．
一十一．解直角三角形的应用-方向角问题（共1小题）
14．（2021•鞍山）小明和小华约定一同去公园游玩，公园有南北两个门，北门A在南门B的正北方向，小明自公园北门A处出发，沿南偏东30°方向前往游乐场D处；小华自南门B处出发，沿正东方向行走150m到达C处，再沿北偏东22.6°方向前往游乐场D处与小明汇合（如图所示），两人所走的路程相同．求公园北门A与南门B之间的距离．（结果取整数．参考数据：sin22.6°≈，cos22.6°≈，tan22.6°≈，≈1.732）

【答案】1293 m．
【解答】解：作DE⊥AB于E，CF⊥DE于F，
∵BC⊥AB，
∴四边形BCFE是矩形，
∴BE＝CF，EF＝BC＝150 m，
设DF＝xm，则DE＝（x+150）m，
在Rt△ADE中，∠BAD＝30°，
∴AD＝2DE＝2（x+150）m，
在Rt△DCF中，∠FCD＝22.6°，
∴CD＝≈＝xm，
∵AD＝CD+BC，
∴2（x+150）＝+150，
解得x＝250（m），
∴DF＝250 m，
∴DE＝250+150＝400 m，
∴AD＝2DE＝800 m，
∴CD＝800﹣150＝650 m，
由勾股定理得AE＝＝＝400 m，
BE＝CF＝＝＝600 m，
∴AB＝AE+BE＝400+600≈1293（m），
答：公园北门A与南门B之间的距离约为1293 m．

一十二．列表法与树状图法（共1小题）
15．（2023•鞍山）二十四节气是中国古代一种用来指导农事的补充历法，在国际气象界被誉为“中国的第五大发明”，并位列联合国教科文组织人类非物质文化遗产代表作名录，小明和小亮对二十四节气非常感兴趣，在课间玩游戏时，准备了四张完全相同的不透明卡片，卡片正面分别写有“A．惊蛰”“B．夏至”“C．白露”“D．霜降”四个节气，两人商量将卡片背面朝上洗匀后，从中随机抽取一张，并讲述所抽卡片上的节气的由来与习俗．
（1）小明从四张卡片中随机抽取一张卡片，抽到“A．惊蛰”的概率是 　　．
（2）小明先从四张卡片中随机抽取一张，小亮再从剩下的卡片中随机抽取一张，请用列表或画树状图的方法，求两人都没有抽到“B．夏至”的概率．
【答案】（1）；
（2）．
【解答】解：（1）共有4种等可能出现的结果，其中抽到“A．惊蛰”的只有1种，
所以小明从四张卡片中随机抽取一张卡片，抽到“A．惊蛰”的概率是，
故答案为：；
（2）用树状图表示所有等可能出现的结果如下：

共有12种等可能出现的结果，其中两人都没有抽到“B．夏至”的有6种，
所以两人都没有抽到“B．夏至”的概率为＝．