

辽宁省本溪市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
展开辽宁省本溪市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
一.相反数(共2小题)
1.(2022•辽宁)5的相反数是( )
A.﹣5 B.﹣ C.5 D.
2.(2022•威海)﹣5的相反数是( )
A.﹣5 B.5 C. D.﹣
二.绝对值(共1小题)
3.(2023•辽宁)2的绝对值是( )
A.﹣ B. C.﹣2 D.2
三.同底数幂的除法(共2小题)
4.(2022•辽宁)下列运算正确的是( )
A.(a2)4=a6 B.a2•a4=a6 C.a2+a4=a6 D.a2÷a4=a6
5.(2021•辽宁)下列运算正确的是( )
A.x2•x=2x2 B.(xy3)2=x2y6
C.x6÷x3=x2 D.x2+x=x3
四.完全平方公式(共1小题)
6.(2023•辽宁)下列运算正确的是( )
A.a+2a2=3a3 B.a7÷a4=a3
C.(a﹣2)2=a2﹣4 D.(3b)2=6b2
五.由实际问题抽象出二元一次方程组(共1小题)
7.(2022•辽宁)《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,木长多少尺?若设绳子长x尺,木长y尺,所列方程组正确的是( )
A. B.
C. D.
六.根的判别式(共1小题)
8.(2022•辽宁)下列一元二次方程无实数根的是( )
A.x2+x﹣2=0 B.x2﹣2x=0 C.x2+x+5=0 D.x2﹣2x+1=0
七.由实际问题抽象出分式方程(共1小题)
9.(2023•辽宁)某校八年级学生去距离学校120km的游览区游览,一部分学生乘慢车先行,出发1h后,另一部分学生乘快车前往,结果他们同时到达.已知快车的速度是慢车速度的1.5倍,求慢车的速度.设慢车的速度是xkm/h,所列方程正确的是( )
A.+1= B.﹣1=
C.= D.=
八.动点问题的函数图象(共2小题)
10.(2023•辽宁)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm.动点P从点A出发,以1cm/s的速度沿射线AB匀速运动,到点B停止运动,同时动点Q从点A出发,以cm/s的速度沿射线AC匀速运动.当点P停止运动时,点Q也随之停止运动.在PQ的右侧以PQ为边作菱形PQMN,点N在射线AB上.设点P的运动时间为x(s),菱形PQMN与△ABC 的重叠部分的面积为y(cm2),则能大致反映y与x之间函数关系的图象是( )
A.
B.
C.
D.
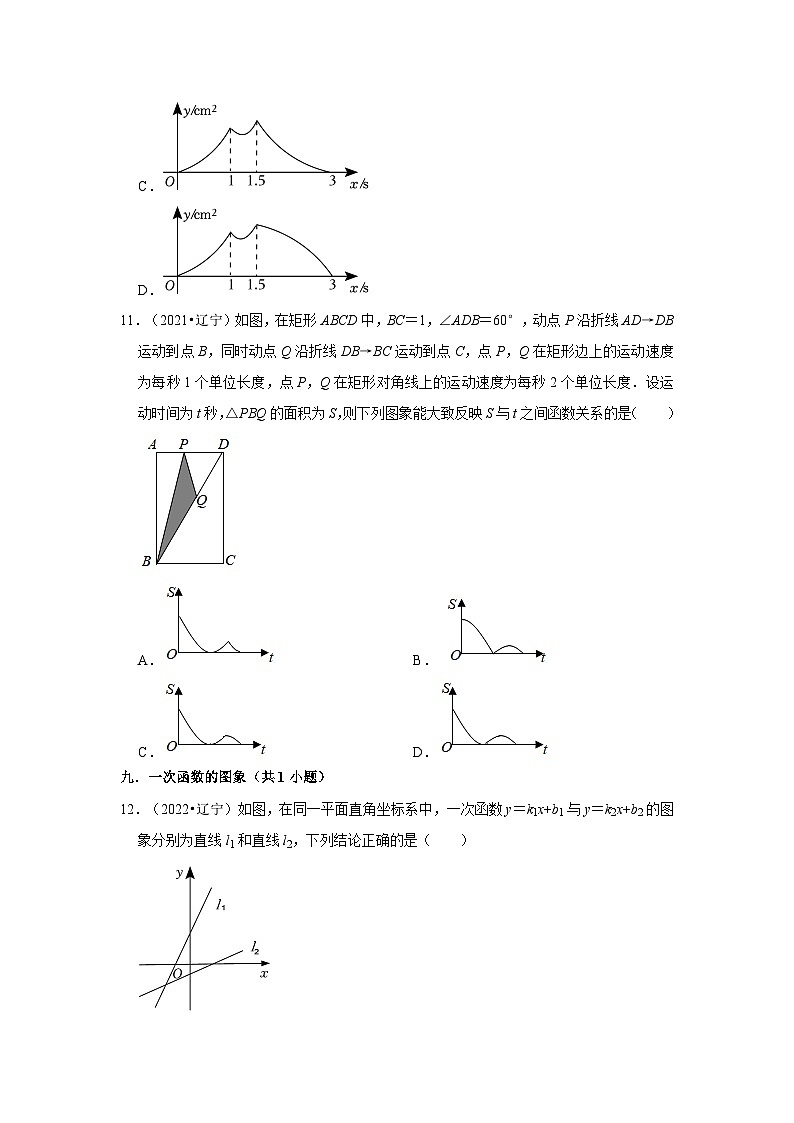
11.(2021•辽宁)如图,在矩形ABCD中,BC=1,∠ADB=60°,动点P沿折线AD→DB运动到点B,同时动点Q沿折线DB→BC运动到点C,点P,Q在矩形边上的运动速度为每秒1个单位长度,点P,Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒,△PBQ的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
九.一次函数的图象(共1小题)
12.(2022•辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,下列结论正确的是( )
A.k1•k2<0 B.k1+k2<0 C.b1﹣b2<0 D.b1•b2<0
一十.反比例函数的性质(共1小题)
13.(2021•辽宁)反比例函数y=的图象分别位于第二、四象限,则直线y=kx+k不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
一十一.二次函数图象与系数的关系(共1小题)
14.(2022•辽宁)抛物线y=ax2+bx+c的部分图象如图所示,对称轴为直线x=﹣1,直线y=kx+c与抛物线都经过点(﹣3,0).下列说法:①ab>0;②4a+c>0;③若(﹣2,y1)与(,y2)是抛物线上的两个点,则y1<y2;④方程ax2+bx+c=0的两根为x1=﹣3,x2=1;⑤当x=﹣1时,函数y=ax2+(b﹣k)x有最大值.其中正确的个数是( )
A.2 B.3 C.4 D.5
一十二.平行线的性质(共1小题)
15.(2023•辽宁)如图,直线CD,EF被射线OA,OB所截,CD∥EF,若∠1=108°,则∠2的度数为( )
A.52° B.62° C.72° D.82°
一十三.三角形的外角性质(共1小题)
16.(2021•辽宁)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
一十四.等腰三角形的性质(共1小题)
17.(2021•辽宁)如图,在△ABC中,AB=BC,由图中的尺规作图痕迹得到的射线BD与AC交于点E,点F为BC的中点,连接EF,若BE=AC=2,则△CEF的周长为( )
A.+1 B.+3 C.+1 D.4
一十五.作图—基本作图(共1小题)
18.(2023•辽宁)如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,以点A为圆心,适当长为半径作弧,分别交AB,AC于点E,F,分别以点E,F为圆心,大于EF的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,则BD的长为( )
A. B. C. D.
一十六.中心对称图形(共3小题)
19.(2023•辽宁)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
20.(2022•辽宁)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
21.(2021•辽宁)下列漂亮的图案中似乎包含了一些曲线,其实它们这种神韵是由多条线段呈现出来的,这些图案中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
一十七.简单几何体的三视图(共1小题)
22.(2023•辽宁)如图所示,该几何体的俯视图是( )
A. B. C. D.
一十八.简单组合体的三视图(共2小题)
23.(2022•辽宁)如图是由6个完全相同的小正方体搭成的几何体,这个几何体的俯视图是( )
A. B.
C. D.
24.(2021•辽宁)如图,该几何体的左视图是( )
A. B.
C. D.
一十九.全面调查与抽样调查(共1小题)
25.(2023•辽宁)下列调查中,适宜采用全面调查方式的是( )
A.了解某种灯泡的使用寿命
B.了解一批冷饮的质量是否合格
C.了解全国八年级学生的视力情况
D.了解某班同学中哪个月份出生的人数最多
二十.折线统计图(共1小题)
26.(2021•辽宁)如图为本溪、辽阳6月1日至5日最低气温的折线统计图,由此可知本溪,辽阳两地这5天最低气温波动情况是( )
A.本溪波动大 B.辽阳波动大
C.本溪、辽阳波动一样 D.无法比较
二十一.中位数(共2小题)
27.(2023•辽宁)在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如下表所示:
成绩/m
1.40
1.50
1.60
1.70
1.80
人数/名
1
3
2
3
1
则这10名运动员成绩的中位数是( )
A.1.50m B.1.55m C.1.60m D.1.65m
28.(2021•辽宁)下表是有关企业和世界卫生组织统计的5种新冠疫苗的有效率,则这5种疫苗有效率的中位数是( )
疫苗名称
克尔来福
阿斯利康
莫德纳
辉瑞
卫星V
有效率
79%
76%
95%
95%
92%
A.79% B.92% C.95% D.76%
二十二.众数(共1小题)
29.(2022•辽宁)一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
所售30双女鞋尺码的众数是( )
A.25cm B.24cm C.23.5cm D.23cm
二十三.方差(共1小题)
30.(2022•辽宁)甲、乙两人在相同的条件下各射击10次,将每次命中的环数绘制成如图所示统计图.根据统计图得出的结论正确的是( )
A.甲的射击成绩比乙的射击成绩更稳定
B.甲射击成绩的众数大于乙射击成绩的众数
C.甲射击成绩的平均数大于乙射击成绩的平均数
D.甲射击成绩的中位数大于乙射击成绩的中位数
辽宁省本溪市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
参考答案与试题解析
一.相反数(共2小题)
1.(2022•辽宁)5的相反数是( )
A.﹣5 B.﹣ C.5 D.
【答案】A
【解答】解:5的相反数是﹣5,
故选:A.
2.(2022•威海)﹣5的相反数是( )
A.﹣5 B.5 C. D.﹣
【答案】B
【解答】解:﹣5的相反数是5.
故选:B.
二.绝对值(共1小题)
3.(2023•辽宁)2的绝对值是( )
A.﹣ B. C.﹣2 D.2
【答案】D
【解答】解:∵2>0,
∴|2|=2.
故选:D.
三.同底数幂的除法(共2小题)
4.(2022•辽宁)下列运算正确的是( )
A.(a2)4=a6 B.a2•a4=a6 C.a2+a4=a6 D.a2÷a4=a6
【答案】B
【解答】解:A.(a2)4=a8,故A选项错误;
B.a2•a4=a6,故B选项正确;
C.a2+a4≠a6,故C选项错误;
D.a2÷a4=a﹣2=,故D选项错误;
故选:B.
5.(2021•辽宁)下列运算正确的是( )
A.x2•x=2x2 B.(xy3)2=x2y6
C.x6÷x3=x2 D.x2+x=x3
【答案】B
【解答】解:A.x2•x=x3,故此选项不符合题意;
B.(xy3)2=x2y6,计算正确,故此选项符合题意;
C.x6÷x3=x3,故此选项不符合题意;
D.x2,x不是同类项,不能合并计算,故此选项不符合题意;
故选:B.
四.完全平方公式(共1小题)
6.(2023•辽宁)下列运算正确的是( )
A.a+2a2=3a3 B.a7÷a4=a3
C.(a﹣2)2=a2﹣4 D.(3b)2=6b2
【答案】B
【解答】解:A.a和2a2不能合并了,故本选项不符合题意;
B.a7÷a4=a3,故本选项符合题意;
C.(a﹣2)2=a2﹣4a+4,故本选项不符合题意;
D.(3b)2=9b2,故本选项不符合题意;
故选:B.
五.由实际问题抽象出二元一次方程组(共1小题)
7.(2022•辽宁)《孙子算经》中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,木长多少尺?若设绳子长x尺,木长y尺,所列方程组正确的是( )
A. B.
C. D.
【答案】C
【解答】解:∵用一根绳子去量一根长木,绳子还剩余4.5尺,
∴x﹣y=4.5;
∵将绳子对折再量长木,长木还剩余1尺,
∴x+1=y.
∴所列方程组为.
故选:C.
六.根的判别式(共1小题)
8.(2022•辽宁)下列一元二次方程无实数根的是( )
A.x2+x﹣2=0 B.x2﹣2x=0 C.x2+x+5=0 D.x2﹣2x+1=0
【答案】C
【解答】解:A、Δ=12﹣4×1×(﹣2)=9>0,则该方程有两个不相等的实数根,故本选项不符合题意;
B、Δ=(﹣2)2﹣4×1×0=4>0,则该方程有两个不相等的实数根,故本选项不符合题意;
C、Δ=12﹣4×1×5=﹣19<0,则该方程无实数根,故本选项符合题意;
D、Δ=(﹣2)2﹣4×1×1=0,则该方程有两个相等的实数根,故本选项不符合题意;
故选:C.
七.由实际问题抽象出分式方程(共1小题)
9.(2023•辽宁)某校八年级学生去距离学校120km的游览区游览,一部分学生乘慢车先行,出发1h后,另一部分学生乘快车前往,结果他们同时到达.已知快车的速度是慢车速度的1.5倍,求慢车的速度.设慢车的速度是xkm/h,所列方程正确的是( )
A.+1= B.﹣1=
C.= D.=
【答案】B
【解答】解:设慢车的速度为xkm/h,
根据题意可列方程为:﹣1=.
故选:B.
八.动点问题的函数图象(共2小题)
10.(2023•辽宁)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm.动点P从点A出发,以1cm/s的速度沿射线AB匀速运动,到点B停止运动,同时动点Q从点A出发,以cm/s的速度沿射线AC匀速运动.当点P停止运动时,点Q也随之停止运动.在PQ的右侧以PQ为边作菱形PQMN,点N在射线AB上.设点P的运动时间为x(s),菱形PQMN与△ABC 的重叠部分的面积为y(cm2),则能大致反映y与x之间函数关系的图象是( )
A.
B.
C.
D.
【答案】A
【解答】解:作PD⊥AC于点D,作QE⊥AB于点E,
由题意得AP=x,AQ=x,
∴AD=AP•cos30°=x,
∴AD=DQ=AQ,
∴PD是线段AQ的垂直平分线,
∴∠PQA=∠A=30°,
∴∠QPE=60°,PQ=AP=x,
∴QE=AQ=x,PQ=PN=MN=QM=x,
当点M运动到直线BC上时,
此时,△BMN是等边三角形,
∴AP=PN=BN=AB=1,x=1;
当点Q、N运动到与点C,B重合时,
∴AP=PN=AB=,x=;
当点P运动到与点B重合时,
∴AP=AB=3,x=3;
∴当0<x≤1时,y=x•x=x2,
当1<x≤时,如图,作FG⊥AB于点G,交QM于点R,
则BN=FN=FB=3﹣2x,FM=MS=FS=3x﹣3,FR=(3x﹣3),
∴y=x2﹣(3x﹣3)•(3x﹣3)=﹣x2+x﹣,
当<x<3时,如图,作HI⊥AB于点I,
则BP=PH=HB=3﹣x,HI=(3﹣x),
∴y=•(3﹣x)•(3﹣x)=x2﹣x+,
综上,y与x之间函数关系的图象分为三段,当0<x≤1时,是开口向上的一段抛物线,当1<x≤时,是开口向下的一段抛物线,当<x<3时,是开口向上的一段抛物线,
只有选项A符合题意,
故选:A.
11.(2021•辽宁)如图,在矩形ABCD中,BC=1,∠ADB=60°,动点P沿折线AD→DB运动到点B,同时动点Q沿折线DB→BC运动到点C,点P,Q在矩形边上的运动速度为每秒1个单位长度,点P,Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒,△PBQ的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A. B.
C. D.
【答案】D
【解答】解:∵四边形ABCD是矩形,
∴AD=BC=1,∠A=∠C=90°,AD∥BC,
∴∠ADB=∠DBC=60°,
∴∠ABD=∠CDB=30°,
∴BD=2AD=2,
当点P在AD上时,S=•(2﹣2t)•(1﹣t)•sin60°=(1﹣t)2(0<t<1),
当点P在线段BD上时,S=[2﹣2(t﹣1)]•(t﹣1)=﹣t2+t﹣(1<t≤2),
观察图象可知,选项D满足条件,
故选:D.
九.一次函数的图象(共1小题)
12.(2022•辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,下列结论正确的是( )
A.k1•k2<0 B.k1+k2<0 C.b1﹣b2<0 D.b1•b2<0
【答案】D
【解答】解:∵一次函数y=k1x+b1的图象过一、二、三象限,
∴k1>0,b1>0,
∵一次函数y=k2x+b2的图象过一、三、四象限,
∴k2>0,b2<0,
∴A、k1•k2>0,故A不符合题意;
B、k1+k2>0,故B不符合题意;
C、b1﹣b2>0,故C不符合题意;
D、b1•b2<0,故D符合题意;
故选:D.
一十.反比例函数的性质(共1小题)
13.(2021•辽宁)反比例函数y=的图象分别位于第二、四象限,则直线y=kx+k不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【解答】解:∵反比例函数y=的图象分别位于第二、四象限,
∴k<0,
∴一次函数y=kx+k的图象经过第二、三、四象限,即不经过第一象限.
故选:A.
一十一.二次函数图象与系数的关系(共1小题)
14.(2022•辽宁)抛物线y=ax2+bx+c的部分图象如图所示,对称轴为直线x=﹣1,直线y=kx+c与抛物线都经过点(﹣3,0).下列说法:①ab>0;②4a+c>0;③若(﹣2,y1)与(,y2)是抛物线上的两个点,则y1<y2;④方程ax2+bx+c=0的两根为x1=﹣3,x2=1;⑤当x=﹣1时,函数y=ax2+(b﹣k)x有最大值.其中正确的个数是( )
A.2 B.3 C.4 D.5
【答案】A
【解答】解:∵抛物线的开口方向向下,
∴a<0.
∵抛物线的对称轴为直线x=﹣1,
∴﹣=﹣1,
∴b=2a,b<0.
∵a<0,b<0,
∴ab>0,
∴①的结论正确;
∵抛物线y=ax2+bx+c经过点(﹣3,0),
∴9a﹣3b+c=0,
∴9a﹣3×2a+c=0,
∴3a+c=0.
∴4a+c=a<0,
∴②的结论不正确;
∵抛物线的对称轴为直线x=﹣1,
∴点(﹣2,y1)关于直线x=﹣1对称的对称点为(0,y1),
∵a<0,
∴当x>﹣1时,y随x的增大而减小.
∵>0>﹣1,
∴y1>y2.
∴③的结论不正确;
∵抛物线的对称轴为直线x=﹣1,抛物线经过点(﹣3,0),
∴抛物线一定经过点(1,0),
∴抛物线y=ax2+bx+c与x轴的交点的横坐标为﹣3,1,
∴方程ax2+bx+c=0的两根为x1=﹣3,x2=1,
∴④的结论正确;
∵直线y=kx+c经过点(﹣3,0),
∴﹣3k+c=0,
∴c=3k.
∵3a+c=0,
∴c=﹣3a,
∴3k=﹣3a,
∴k=﹣a.
∴函数y=ax2+(b﹣k)x
=ax2+(2a+a)x
=ax2+3ax
=a﹣a,
∵a<0,
∴当x=﹣时,函数y=ax2+(b﹣k)x有最大值,
∴⑤的结论不正确.
综上,结论正确的有:①④,
故选:A.
一十二.平行线的性质(共1小题)
15.(2023•辽宁)如图,直线CD,EF被射线OA,OB所截,CD∥EF,若∠1=108°,则∠2的度数为( )
A.52° B.62° C.72° D.82°
【答案】C
【解答】解:如图:
∵CD∥EF,
∴∠2+∠3=180°,
∵∠1=∠3,
∴∠1+∠2=180°,
∵∠1=108°,
∴∠2=72°,
故选:C.
一十三.三角形的外角性质(共1小题)
16.(2021•辽宁)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
【答案】B
【解答】解:如图,∠5=90°﹣30°=60°,∠3=∠1﹣45°=35°,
∴∠4=∠3=35°,
∴∠2=∠4+∠5=95°,
故选:B.
一十四.等腰三角形的性质(共1小题)
17.(2021•辽宁)如图,在△ABC中,AB=BC,由图中的尺规作图痕迹得到的射线BD与AC交于点E,点F为BC的中点,连接EF,若BE=AC=2,则△CEF的周长为( )
A.+1 B.+3 C.+1 D.4
【答案】C
【解答】解:由图中的尺规作图得:BE是∠ABC的平分线,
∵AB=BC,
∴BE⊥AC,AE=CE=AC=1,
∴∠BEC=90°,
∴BC===,
∵点F为BC的中点,
∴EF=BC=BF=CF,
∴△CEF的周长=CF+EF+CE=CF+BF+CE=BC+CE=+1,
故选:C.
一十五.作图—基本作图(共1小题)
18.(2023•辽宁)如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,以点A为圆心,适当长为半径作弧,分别交AB,AC于点E,F,分别以点E,F为圆心,大于EF的长为半径作弧,两弧在∠BAC的内部相交于点G,作射线AG,交BC于点D,则BD的长为( )
A. B. C. D.
【答案】D
【解答】解:作DM⊥AB于M,
由题意知AD平分∠BAC,
∵DC⊥AC,
∴CD=DM,
∵∠C=90°,AB=5,BC=3,
∴AC==4,
∵△ABC的面积=△ACD的面积+△ABD的面积,
∴AC•BC=AC•CD+AB•MD,
∴4×3=4CD+5CD,
∴CD=,
∴BD=BC﹣CD=3﹣=.
故选:D.
一十六.中心对称图形(共3小题)
19.(2023•辽宁)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【答案】A
【解答】解:A、原图既是中心对称图形,又是轴对称图形,故此选项符合题意;
B、原图不是中心对称图形,是轴对称图形,故此选项不合题意;
C、原图不是中心对称图形,是轴对称图形,故此选项不合题意;
D、原图不是中心对称图形,是轴对称图形,故此选项不合题意;
故选:A.
20.(2022•辽宁)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【答案】D
【解答】解:A.不是中心对称图形,也不是轴对称图形,故此选项不合题意;
B.不是中心对称图形,是轴对称图形,故此选项不合题意;
C.是中心对称图形,不是轴对称图形,故此选项不合题意;
D.是中心对称图形,也是轴对称图形,故此选项符合题意;
故选:D.
21.(2021•辽宁)下列漂亮的图案中似乎包含了一些曲线,其实它们这种神韵是由多条线段呈现出来的,这些图案中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
【答案】A
【解答】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.是轴对称图形,不是中心对称图形,故本选项不合题意;
D.是轴对称图形,不是中心对称图形,故本选项不合题意.
故选:A.
一十七.简单几何体的三视图(共1小题)
22.(2023•辽宁)如图所示,该几何体的俯视图是( )
A. B. C. D.
【答案】C
【解答】解:从上面看得该几何体的俯视图是:
.
故选:C.
一十八.简单组合体的三视图(共2小题)
23.(2022•辽宁)如图是由6个完全相同的小正方体搭成的几何体,这个几何体的俯视图是( )
A. B.
C. D.
【答案】B
【解答】解:从上面看,底层右边是一个小正方形,上层是三个小正方形,
故选:B.
24.(2021•辽宁)如图,该几何体的左视图是( )
A. B.
C. D.
【答案】D
【解答】解:从左面看该几何体所得到的图形是一个长方形,被挡住的棱用虚线表示,图形如下:
故选:D.
一十九.全面调查与抽样调查(共1小题)
25.(2023•辽宁)下列调查中,适宜采用全面调查方式的是( )
A.了解某种灯泡的使用寿命
B.了解一批冷饮的质量是否合格
C.了解全国八年级学生的视力情况
D.了解某班同学中哪个月份出生的人数最多
【答案】D
【解答】解:A、了解某种灯泡的使用寿命,适宜采用抽样调查方式,故此选项不符合题意;
B、了解一批冷饮的质量是否合格,适宜采用抽样调查方式,故此选项不符合题意;
C、了解全国八年级学生的视力情况,适宜采用抽样调查方式,故此选项不符合题意;
D、了解某班同学中哪个月份出生的人数最多,适宜采用全面调查方式,故此选项符合题意;
故选:D.
二十.折线统计图(共1小题)
26.(2021•辽宁)如图为本溪、辽阳6月1日至5日最低气温的折线统计图,由此可知本溪,辽阳两地这5天最低气温波动情况是( )
A.本溪波动大 B.辽阳波动大
C.本溪、辽阳波动一样 D.无法比较
【答案】C
【解答】解:本溪6月1日至5日最低气温的平均数为=12.8(℃),
辽阳6月1日至5日最低气温的平均数为=13.8(℃);
本溪6月1日至5日最低气温的方差S12=×[(12﹣12.8)2×3+(15﹣12.8)2+(13﹣12.8)2]=1.36,
辽阳6月1日至5日最低气温的方差S22=×[(13﹣13.8)2×3+(16﹣13.8)2+(14﹣13.8)2]=1.36,
∵S12=S22,
∴本溪、辽阳波动一样.
故选:C.
二十一.中位数(共2小题)
27.(2023•辽宁)在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如下表所示:
成绩/m
1.40
1.50
1.60
1.70
1.80
人数/名
1
3
2
3
1
则这10名运动员成绩的中位数是( )
A.1.50m B.1.55m C.1.60m D.1.65m
【答案】C
【解答】解:中位数是按从小到大排列后第5,第6两个数的平均数作为中位数,
故这组数据的中位数×(1.60+1.60)=1.60.
故选:C.
28.(2021•辽宁)下表是有关企业和世界卫生组织统计的5种新冠疫苗的有效率,则这5种疫苗有效率的中位数是( )
疫苗名称
克尔来福
阿斯利康
莫德纳
辉瑞
卫星V
有效率
79%
76%
95%
95%
92%
A.79% B.92% C.95% D.76%
【答案】B
【解答】解:从小到大排列此数据为:76%、79%、92%、95%、95%,92%处在第3位为中位数.
故选:B.
二十二.众数(共1小题)
29.(2022•辽宁)一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
所售30双女鞋尺码的众数是( )
A.25cm B.24cm C.23.5cm D.23cm
【答案】C
【解答】解:因为众数是在一组数据中出现次数最多的数,23.5出现的次数最多,
∴众数是23.5cm.
故选:C.
二十三.方差(共1小题)
30.(2022•辽宁)甲、乙两人在相同的条件下各射击10次,将每次命中的环数绘制成如图所示统计图.根据统计图得出的结论正确的是( )
A.甲的射击成绩比乙的射击成绩更稳定
B.甲射击成绩的众数大于乙射击成绩的众数
C.甲射击成绩的平均数大于乙射击成绩的平均数
D.甲射击成绩的中位数大于乙射击成绩的中位数
【答案】A
【解答】解:由图可得,甲射击10次的成绩分别为5,6,6,7,5,6,6,6,7,6;乙射击10次的成绩分别为9,5,3,6,9,10,4,7,8,9.
甲的成绩起伏比乙的成绩起伏小,故A正确,符合题意;
甲的众数是6,乙的众数是9,故B错误,不符合题意;
甲的平均数为×(5+6+6+7+5+6+6+6+7+6)=6,乙的平均数为×(9+5+3+6+9+10+4+7+8+9)=7,故C错误,不符合题意;
甲的中位数是6,乙的中位数是7.5,故D错误,不符合题意.
故选:A.
辽宁省盘锦市2021-2023三年中考数学真题分类汇编-01选择题知识点分类: 这是一份辽宁省盘锦市2021-2023三年中考数学真题分类汇编-01选择题知识点分类,共27页。
辽宁省抚顺市2021-2023三年中考数学真题分类汇编-01选择题知识点分类: 这是一份辽宁省抚顺市2021-2023三年中考数学真题分类汇编-01选择题知识点分类,共29页。
辽宁省大连市2021-2023三年中考数学真题分类汇编-01选择题知识点分类: 这是一份辽宁省大连市2021-2023三年中考数学真题分类汇编-01选择题知识点分类,共19页。












