
辽宁省本溪市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
展开辽宁省本溪市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一.科学记数法—表示较大的数(共2小题)
1.(2023•辽宁)截止到2023年4月底,我国5G网络覆盖全国所有地级(以上)市、县城城区,5G移动电话用户达到634000000户,将数据634000000用科学记数法表示为 .
2.(2022•辽宁)2022年北京冬奥会全冰面速滑馆的冰面面积约为12000平方米,为亚洲最大,将数据12000用科学记数法表示为 .
二.提公因式法与公式法的综合运用(共3小题)
3.(2023•辽宁)分解因式:m3﹣4m2+4m= .
4.(2022•辽宁)分解因式:ax2﹣a= .
5.(2023•怀化)分解因式:2x2﹣4x+2= .
三.二次根式有意义的条件(共1小题)
6.(2021•辽宁)若在实数范围内有意义,则x的取值范围是 .
四.根的判别式(共2小题)
7.(2023•辽宁)若关于x的一元二次方程x2﹣x+k+1=0有两个实数根,则k的取值范围是 .
8.(2021•辽宁)若关于x的一元二次方程3x2﹣2x﹣k=0有两个相等的实数根,则k的值为 .
五.由实际问题抽象出分式方程(共1小题)
9.(2021•辽宁)为了弘扬我国书法艺术,培养学生良好的书写能力,某校举办了书法比赛,学校准备为获奖同学颁奖.在购买奖品时发现,A种奖品的单价比B种奖品的单价多10元,用300元购买A种奖品的数量与用240元购买B种奖品的数量相同.设B种奖品的单价是x元,则可列分式方程为 .
六.反比例函数系数k的几何意义(共1小题)
10.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为 .
七.反比例函数图象上点的坐标特征(共2小题)
11.(2022•辽宁)反比例函数y=的图象经过点A(1,3),则k的值是 .
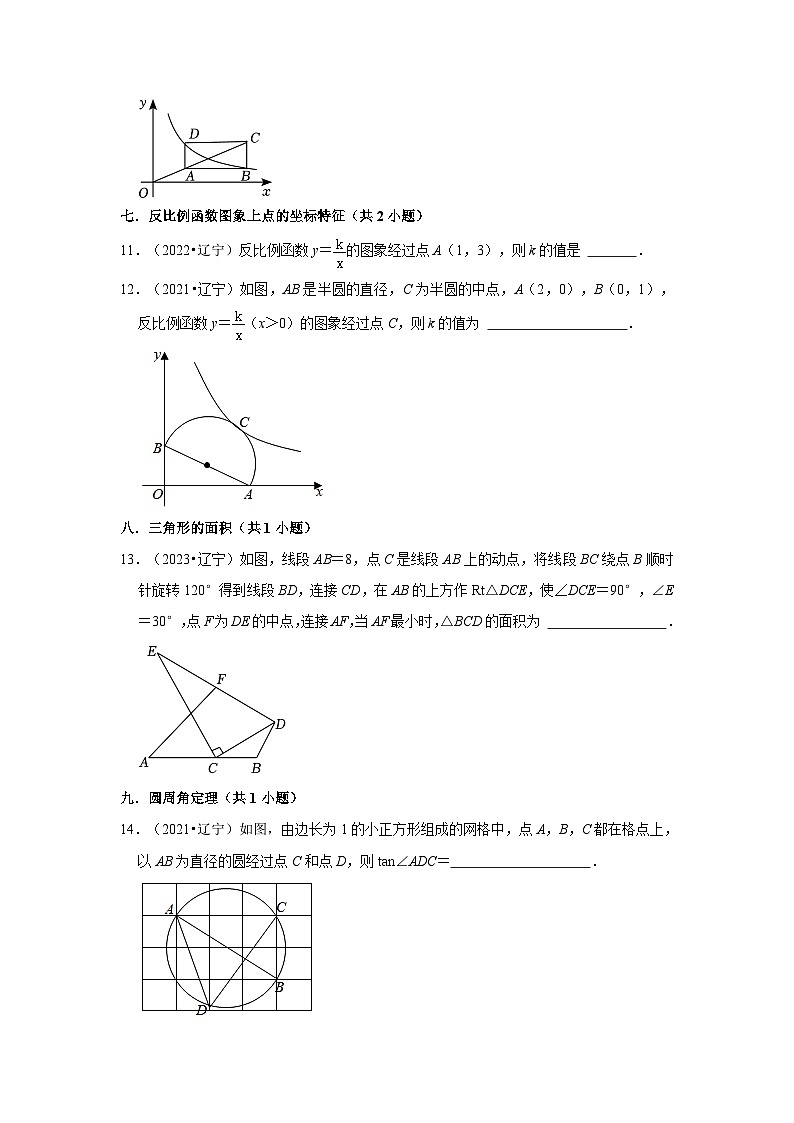
12.(2021•辽宁)如图,AB是半圆的直径,C为半圆的中点,A(2,0),B(0,1),反比例函数y=(x>0)的图象经过点C,则k的值为 .
八.三角形的面积(共1小题)
13.(2023•辽宁)如图,线段AB=8,点C是线段AB上的动点,将线段BC绕点B顺时针旋转120°得到线段BD,连接CD,在AB的上方作Rt△DCE,使∠DCE=90°,∠E=30°,点F为DE的中点,连接AF,当AF最小时,△BCD的面积为 .
九.圆周角定理(共1小题)
14.(2021•辽宁)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC= .
一十.作图—基本作图(共1小题)
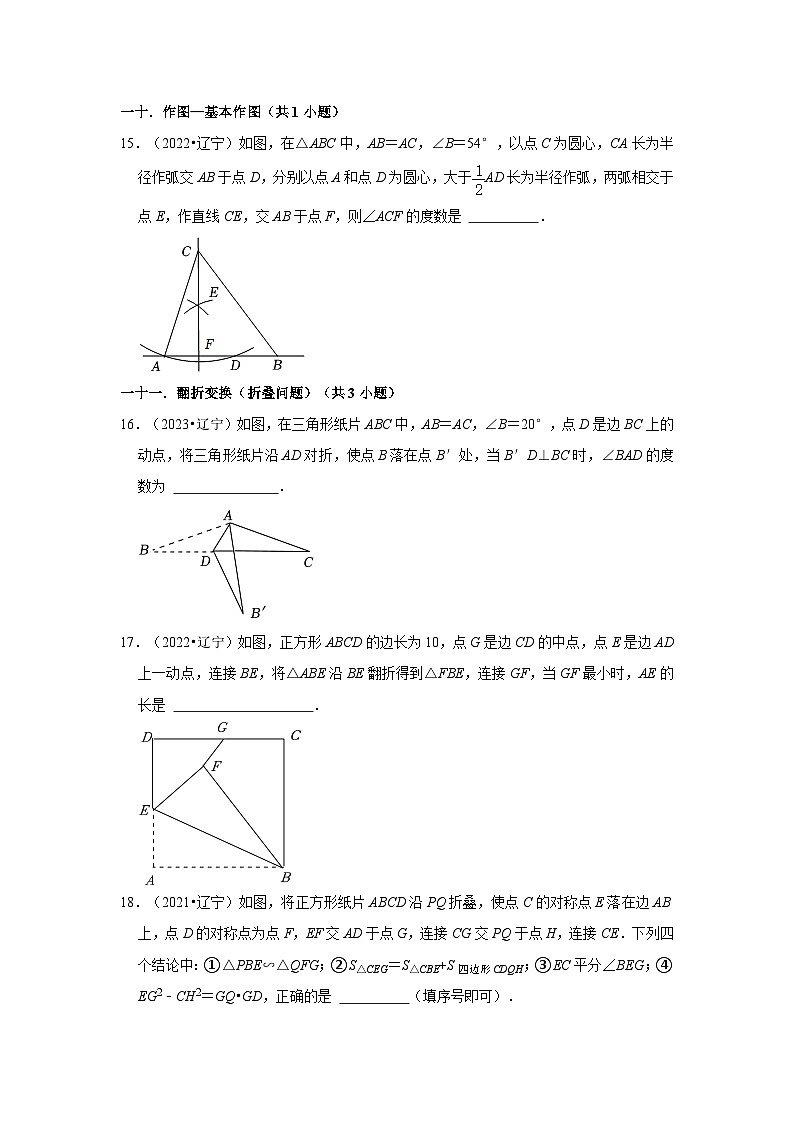
15.(2022•辽宁)如图,在△ABC中,AB=AC,∠B=54°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则∠ACF的度数是 .
一十一.翻折变换(折叠问题)(共3小题)
16.(2023•辽宁)如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D是边BC上的动点,将三角形纸片沿AD对折,使点B落在点B′处,当B′D⊥BC时,∠BAD的度数为 .
17.(2022•辽宁)如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,当GF最小时,AE的长是 .
18.(2021•辽宁)如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是 (填序号即可).
一十二.坐标与图形变化-平移(共1小题)
19.(2022•辽宁)在平面直角坐标系中,线段AB的端点A(3,2),B(5,2),将线段AB平移得到线段CD,点A的对应点C的坐标是(﹣1,2),则点B的对应点D的坐标是 .
一十三.相似三角形的判定与性质(共1小题)
20.(2022•辽宁)如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,点P为斜边AB上的一个动点(点P不与点A、B重合),过点P作PD⊥AC,PE⊥BC,垂足分别为点D和点E,连接DE,PC交于点Q,连接AQ,当△APQ为直角三角形时,AP的长是 .
一十四.位似变换(共1小题)
21.(2023•辽宁)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(1,0),B(2,3),C(﹣1,2),若四边形OA′B′C′与四边形OABC关于原点O位似,且四边形OA′B′C′的面积是四边形OABC面积的4倍,则第一象限内点B′的坐标为 .
一十五.概率公式(共1小题)
22.(2021•辽宁)有5张看上去无差别的卡片,上面分别写着﹣,﹣1,0,,2.从中随机抽取一张,则抽出卡片上写的数是的概率为 .
一十六.几何概率(共1小题)
23.(2023•辽宁)如图,等边三角形ABC是由9个大小相等的等边三角形构成,随机地往△ABC内投一粒米,落在阴影区域的概率为 .
一十七.利用频率估计概率(共1小题)
24.(2022•辽宁)质检部门对某批产品的质量进行随机抽检,结果如下表所示:
抽检产品数n
100
150
200
250
300
500
1000
合格产品数m
89
134
179
226
271
451
904
合格率
0.890
0.893
0.895
0.904
0.903
0.902
0.904
在这批产品中任取一件,恰好是合格产品的概率约是(结果保留一位小数) .
辽宁省本溪市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一.科学记数法—表示较大的数(共2小题)
1.(2023•辽宁)截止到2023年4月底,我国5G网络覆盖全国所有地级(以上)市、县城城区,5G移动电话用户达到634000000户,将数据634000000用科学记数法表示为 6.34×108 .
【答案】6.34×108.
【解答】解:634000000=6.34×100000000=6.34×108,
故答案为:6.34×108.
2.(2022•辽宁)2022年北京冬奥会全冰面速滑馆的冰面面积约为12000平方米,为亚洲最大,将数据12000用科学记数法表示为 1.2×104 .
【答案】1.2×104.
【解答】解:12000用科学记数法表示为1.2×104.
故答案为:1.2×104.
二.提公因式法与公式法的综合运用(共3小题)
3.(2023•辽宁)分解因式:m3﹣4m2+4m= m(m﹣2)2 .
【答案】见试题解答内容
【解答】解:m3﹣4m2+4m
=m(m2﹣4m+4)
=m(m﹣2)2.
故答案为:m(m﹣2)2.
4.(2022•辽宁)分解因式:ax2﹣a= a(x+1)(x﹣1) .
【答案】a(x+1)(x﹣1).
【解答】解:ax2﹣a,
=a(x2﹣1),
=a(x+1)(x﹣1).
5.(2023•怀化)分解因式:2x2﹣4x+2= 2(x﹣1)2 .
【答案】见试题解答内容
【解答】解:2x2﹣4x+2,
=2(x2﹣2x+1),
=2(x﹣1)2.
三.二次根式有意义的条件(共1小题)
6.(2021•辽宁)若在实数范围内有意义,则x的取值范围是 x≤2 .
【答案】见试题解答内容
【解答】解:由题意得,2﹣x≥0,
解得,x≤2,
故答案为:x≤2.
四.根的判别式(共2小题)
7.(2023•辽宁)若关于x的一元二次方程x2﹣x+k+1=0有两个实数根,则k的取值范围是 k≤﹣ .
【答案】k≤﹣.
【解答】解:根据题意得Δ=(﹣1)2﹣4×(k+1)≥0,
解得k≤﹣.
故答案为:k≤﹣.
8.(2021•辽宁)若关于x的一元二次方程3x2﹣2x﹣k=0有两个相等的实数根,则k的值为 ﹣ .
【答案】﹣.
【解答】解:∵一元二次方程3x2﹣2x﹣k=0有两个相等的实数根,
∴Δ=b2﹣4ac=(﹣2)2﹣4×3×(﹣k)=0,
解得k=﹣.
故答案为﹣.
五.由实际问题抽象出分式方程(共1小题)
9.(2021•辽宁)为了弘扬我国书法艺术,培养学生良好的书写能力,某校举办了书法比赛,学校准备为获奖同学颁奖.在购买奖品时发现,A种奖品的单价比B种奖品的单价多10元,用300元购买A种奖品的数量与用240元购买B种奖品的数量相同.设B种奖品的单价是x元,则可列分式方程为 = .
【答案】=.
【解答】解:设B种奖品的单价是x元,则A种奖品的单价是(x+10)元,
依题意得:=.
故答案为:=.
六.反比例函数系数k的几何意义(共1小题)
10.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为 6 .
【答案】6.
【解答】解:如图,延长CD交y轴于E,连接OD,
∵矩形ABCD的面积是8,
∴S△ADC=4,
∵AC=2AO,
∴S△ADO=2,
∵AD∥OE,
∴△ACD∽△OCE,
∴AD:OE=AC:OC=2:3,
∴S△ODE=3,
由几何意义得,=3,
∵k>0,
∴k=6,
故答案为:6.
七.反比例函数图象上点的坐标特征(共2小题)
11.(2022•辽宁)反比例函数y=的图象经过点A(1,3),则k的值是 3 .
【答案】3.
【解答】解:∵反比例函数y=的图象经过点A(1,3),
∴k=1×3=3,
故答案为:3.
12.(2021•辽宁)如图,AB是半圆的直径,C为半圆的中点,A(2,0),B(0,1),反比例函数y=(x>0)的图象经过点C,则k的值为 .
【答案】.
【解答】解法一、设半圆圆心为D,连接DC,过C作CG⊥OA于G,交AB于E,如图:
∵A(2,0),B(0,1),
∴AB=,DA=DC=,
∴cos∠BAO==,sin∠BAO==,
∵C为半圆的中点,
∴∠CDE=∠EGA=90°,
又∠CED=∠AEG,
∴∠DCE=∠BAO,
Rt△CDE中,cos∠DCE=,
∴=,
∴CE=,
∴DE==
∴AE=AD﹣DE=﹣=,
Rt△AGE中,cos∠BAO==
∴=,
∴AG=,
∴OG=OA﹣AG=,
∴EG==,
∴CG=CE+GE=,
∴C(,),
把C(,)代入y=得k=,
解法二、设半圆圆心为D,连接CB,CA,过点C作CM⊥y轴于点M,CN⊥x轴于点N,如图:
∵点C为半圆的中点,
∴=,∠BCA=90°,
∴BC=AC,
∵CM⊥y轴,CN⊥x轴,
∴∠CMB=∠CNA=90°,∠MCN=90°,
∴∠MCN﹣∠BCN=∠BCA﹣∠BCN,即∠BCM=∠ACN,
∴△BCM≌△ACN(AAS),
∴CM=CN,BM=AN,
∴四边形OMCN是正方形,
∵OA=2,OB=1,
设正方形OMCN的边长为a,由BM=AN得,2﹣a=a﹣1,解得a=,
∴点C的坐标为(,),
∵反比例函数y=(x>0)的图象经过点C,
∴k==.
故答案为:.
八.三角形的面积(共1小题)
13.(2023•辽宁)如图,线段AB=8,点C是线段AB上的动点,将线段BC绕点B顺时针旋转120°得到线段BD,连接CD,在AB的上方作Rt△DCE,使∠DCE=90°,∠E=30°,点F为DE的中点,连接AF,当AF最小时,△BCD的面积为 .
【答案】.
【解答】解:连接CF,则CF=DF=EF,
∵∠EDC=90°﹣∠E=60°,
∴∠FCD=60°.
∵∠DCB=(180°﹣120°)=30°,
∴∠FCB=∠FCD+∠DCB=60°+30°=90°,
∴△ACF是直角三角形.
设BC=x,则AC=8﹣x,BC=BD=x,CD=CF=x,由勾股定理得:
AF===2.
当x=2时,AF有最小值.
∴BC=BD=2,∠CBD=120°,
∴S△BCD=×2×2×=.
故答案为:.
九.圆周角定理(共1小题)
14.(2021•辽宁)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC= .
【答案】.
【解答】解:∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,tan∠ABC==,
∵∠ADC=∠ABC,
∴tan∠ADC=.
故答案为.
一十.作图—基本作图(共1小题)
15.(2022•辽宁)如图,在△ABC中,AB=AC,∠B=54°,以点C为圆心,CA长为半径作弧交AB于点D,分别以点A和点D为圆心,大于AD长为半径作弧,两弧相交于点E,作直线CE,交AB于点F,则∠ACF的度数是 18° .
【答案】见试题解答内容
【解答】解:由作图可得,CF⊥AB于F,
∴∠BFC=90°,
∴∠BCF=90°﹣∠B=36°,
又∵AB=AC,∠B=54°,
∴∠ACB=∠B=54°,
∴∠ACF=54°﹣36°=18°,
故答案为:18°.
一十一.翻折变换(折叠问题)(共3小题)
16.(2023•辽宁)如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D是边BC上的动点,将三角形纸片沿AD对折,使点B落在点B′处,当B′D⊥BC时,∠BAD的度数为 25°或115° .
【答案】25°或115°.
【解答】解:当点B′在直线BC的下方,如图1,
∵B′D⊥BC,
∴∠BDB′=90°,
∴∠ADB′+∠ADB=360°﹣90°=270°,
∵将三角形纸片沿AD对折,使点B落在点B′处,
∴∠ADB′=∠ADB=×270°=135°,
∵∠B=20°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣20°﹣135°=25°;
当点B′在直线BC的上方时,如图2,
∵B′D⊥BC,
∴∠BDB′=90°,
∵将三角形纸片沿AD对折,使点B落在点B′处,
∴∠ADB′=∠ADB=×90°=45°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣20°﹣45°=115°,
故答案为:25°或115°.
17.(2022•辽宁)如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,当GF最小时,AE的长是 5﹣5 .
【答案】5﹣5
【解答】解:∵将△ABE沿BE翻折得到△FBE,
∴BF=BA=10,
∴点F在以B为圆心,10为半径的圆上运动,
∴当点G、F、B三点共线时,GF最小,
连接EG,设AE=x,
由勾股定理得,BG=5,
∵S梯形ABGD=S△EDG+S△ABE+S△EBG,
∴(5+10)×10=++,
解得x=5﹣5,
∴AE=5﹣5,
故答案为:5﹣5.
18.(2021•辽宁)如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是 ①③④ (填序号即可).
【答案】①③④.
【解答】解:①∵四边形ABCD是正方形,
∴∠A=∠B=∠BCD=∠D=90°.
由折叠可知:∠GEP=∠BCD=90°,∠F=∠D=90°.
∴∠BEP+∠AEG=90°,
∵∠A=90°,
∴∠AEG+∠AGE=90°,
∴∠BEP=∠AGE.
∵∠FGQ=∠AGE,
∴∠BEP=∠FGQ.
∵∠B=∠F=90°,
∴△PBE∽△QFG.
故①正确;
②过点C作CM⊥EG于M,
由折叠可得:∠GEC=∠DCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠GEC,
在△BEC和△MEC中,
,
∴△BEC≌△MEC(AAS).
∴CB=CM,S△BEC=S△MEC.
∵CG=CG,
∴Rt△CMG≌Rt△CDG(HL),
∴S△CMG=S△CDG,
∴S△CEG=S△BEC+S△CDG>S△BEC+S四边形CDQH,
∴②不正确;
③由折叠可得:∠GEC=∠DCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BEC=∠GEC,
即EC平分∠BEG.
∴③正确;
④连接DH,MH,HE,如图,
∵△BEC≌△MEC,△CMG≌△CDG,
∴∠BCE=∠MCE,∠MCG=∠DCG,
∴∠ECG=∠ECM+∠GCM=∠BCD=45°,
∵EC⊥HP,
∴∠CHP=45°.
∴∠GHQ=∠CHP=45°.
由折叠可得:∠EHP=∠CHP=45°,
∴EH⊥CG.
∴EG2﹣EH2=GH2.
由折叠可知:EH=CH.
∴EG2﹣CH2=GH2.
∵CM⊥EG,EH⊥CG,
∴∠EMC=∠EHC=90°,
∴E,M,H,C四点共圆,
∴∠HMC=∠HEC=45°.
在△CMH和△CDH中,
,
∴△CMH≌△CDH(SAS).
∴∠CDH=∠CMH=45°,
∵∠CDA=90°,
∴∠GDH=45°,
∵∠GHQ=∠CHP=45°,
∴∠GHQ=∠GDH=45°.
∵∠HGQ=∠DGH,
∴△GHQ∽△GDH,
∴.
∴GH2=GQ•GD.
∴GE2﹣CH2=GQ•GD.
∴④正确;
综上可得,正确的结论有:①③④.
故答案为:①③④.
一十二.坐标与图形变化-平移(共1小题)
19.(2022•辽宁)在平面直角坐标系中,线段AB的端点A(3,2),B(5,2),将线段AB平移得到线段CD,点A的对应点C的坐标是(﹣1,2),则点B的对应点D的坐标是 (1,2) .
【答案】(1,2).
【解答】解:∵点A(3,2)的对应点C的坐标为(﹣1,2),
∴平移规律为向左平移4个单位,
∴B(5,2)的对应点D的坐标为(1,2).
故答案为:(1,2).
一十三.相似三角形的判定与性质(共1小题)
20.(2022•辽宁)如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,点P为斜边AB上的一个动点(点P不与点A、B重合),过点P作PD⊥AC,PE⊥BC,垂足分别为点D和点E,连接DE,PC交于点Q,连接AQ,当△APQ为直角三角形时,AP的长是 3或2 .
【答案】见试题解答内容
【解答】解:在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠BAC=30°,
∴AB=2BC=2×2=4,
∴AC===2,
当∠APQ=90°时,如图1,
在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠BAC=30°,
∴AB=2BC=2×2=4,
∴AC===2,
∴AP=3,
当∠AQP=90°时,如图2,
∵PD⊥AC,PE⊥BC,∠ACB=90°,
∴四边形DPEC是矩形,
∴CQ=QP,
∵∠AQP=90°,
∴AQ垂直平分CP,
∴AP=AC=2,
综上所述,当△APQ为直角三角形时,AP的长是3或2,
故答案为:3或2.
一十四.位似变换(共1小题)
21.(2023•辽宁)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(1,0),B(2,3),C(﹣1,2),若四边形OA′B′C′与四边形OABC关于原点O位似,且四边形OA′B′C′的面积是四边形OABC面积的4倍,则第一象限内点B′的坐标为 (4,6) .
【答案】(4,6).
【解答】解:∵四边形OA′B′C′与四边形OABC关于原点O位似,且四边形OA′B′C′的面积是四边形OABC面积的4倍,
∴四边形OA′B′C′与四边形OABC的位似比是2:1,
∵点B(2,3),
∴第一象限内点B′的坐标为(4,6).
故答案为:(4,6).
一十五.概率公式(共1小题)
22.(2021•辽宁)有5张看上去无差别的卡片,上面分别写着﹣,﹣1,0,,2.从中随机抽取一张,则抽出卡片上写的数是的概率为 .
【答案】.
【解答】解:∵有5张看上去无差别的卡片,上面分别写着﹣,﹣1,0,,2,
∴从中随机抽取一张,抽出卡片上写的数是的概率为1÷5=.
故答案为:.
一十六.几何概率(共1小题)
23.(2023•辽宁)如图,等边三角形ABC是由9个大小相等的等边三角形构成,随机地往△ABC内投一粒米,落在阴影区域的概率为 .
【答案】.
【解答】解:∵总面积为9个大小相等的等边三角形的面积,其中阴影区域面积为5个大小相等的等边三角形的面积,
∴随机地往△ABC内投一粒米,落在阴影区域的概率为.
故答案为:.
一十七.利用频率估计概率(共1小题)
24.(2022•辽宁)质检部门对某批产品的质量进行随机抽检,结果如下表所示:
抽检产品数n
100
150
200
250
300
500
1000
合格产品数m
89
134
179
226
271
451
904
合格率
0.890
0.893
0.895
0.904
0.903
0.902
0.904
在这批产品中任取一件,恰好是合格产品的概率约是(结果保留一位小数) 0.9 .
【答案】0.9.
【解答】解:由表格中的数据可得,
在这批产品中任取一件,恰好是合格产品的概率约是0.9,
故答案为:0.9.
河南省2021-2023三年中考数学真题分类汇编-02填空题知识点分类: 这是一份河南省2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共16页。
辽宁省盘锦市2021-2023三年中考数学真题分类汇编-02填空题知识点分类: 这是一份辽宁省盘锦市2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共20页。试卷主要包含了计算,分解因式等内容,欢迎下载使用。
辽宁省阜新市2021-2023三年中考数学真题分类汇编-02填空题知识点分类: 这是一份辽宁省阜新市2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共15页。试卷主要包含了0= ,计算,﹣1= 等内容,欢迎下载使用。












