

所属成套资源:全国各地区2021-2023三年中考数学真题按题型难易度分层分类汇编
青海省2021-2023三年中考数学真题分类汇编-02填空题知识点分类
展开
这是一份青海省2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共21页。试卷主要包含了﹣3的绝对值是 ,观察下列各等式等内容,欢迎下载使用。
青海省2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一.相反数(共1小题)
1.(2022•青海)﹣2022的相反数是 .
二.绝对值(共1小题)
2.(2023•青海)﹣3的绝对值是 .
三.科学记数法—表示较大的数(共3小题)
3.(2023•青海)青藏联网工程东起青海西宁,西至西藏拉萨,被誉为“电力天路”.截至2023年5月“电力天路”已安全运行近12年,累计向西藏送电105.9亿千瓦时,数据105.9亿用科学记数法表示为 .
4.(2022•青海)习近平总书记指出“善于学习,就是善于进步”.“学习强国”平台上线的某天,全国大约有124600000人在平台上学习,将这个数据用科学记数法表示为 .
5.(2021•青海)5月11日,第七次人口普查结果发布.数据显示,全国人口共14.1178亿人,同2010年第六次全国人口普查数据相比,我国人口10年来继续保持低速增长态势.其中数据“14.1178亿”用科学记数法表示为 .
四.算术平方根(共1小题)
6.(2021•青海)观察下列各等式:
①;
②;
③;
…
根据以上规律,请写出第5个等式: .
五.估算无理数的大小(共1小题)
7.(2023•青海)写出一个比﹣大且比小的整数 .
六.同类项(共1小题)
8.(2021•青海)已知单项式2a4b﹣2m+7与3a2mbn+2是同类项,则m+n= .
七.规律型:图形的变化类(共1小题)
9.(2022•青海)木材加工厂将一批木料按如图所示的规律依次摆放,则第n个图中共有木料 根.
八.二次根式有意义的条件(共1小题)
10.(2022•青海)若式子有意义,则实数x的取值范围是 .
九.一元二次方程的解(共1小题)
11.(2021•青海)已知m是一元二次方程x2+x﹣6=0的一个根,则代数式m2+m的值等于 .
一十.由实际问题抽象出一元二次方程(共1小题)
12.(2022•青海)如图,小明同学用一张长11cm,宽7cm的矩形纸板制作一个底面积为21cm2的无盖长方体纸盒,他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计).设剪去的正方形边长为xcm,则可列出关于x的方程为 .
一十一.解一元一次不等式组(共1小题)
13.(2021•青海)已知点A(2m﹣5,6﹣2m)在第四象限,则m的取值范围是 .
一十二.一元一次不等式组的整数解(共1小题)
14.(2022•青海)不等式组的所有整数解的和为 .
一十三.一次函数图象上点的坐标特征(共1小题)
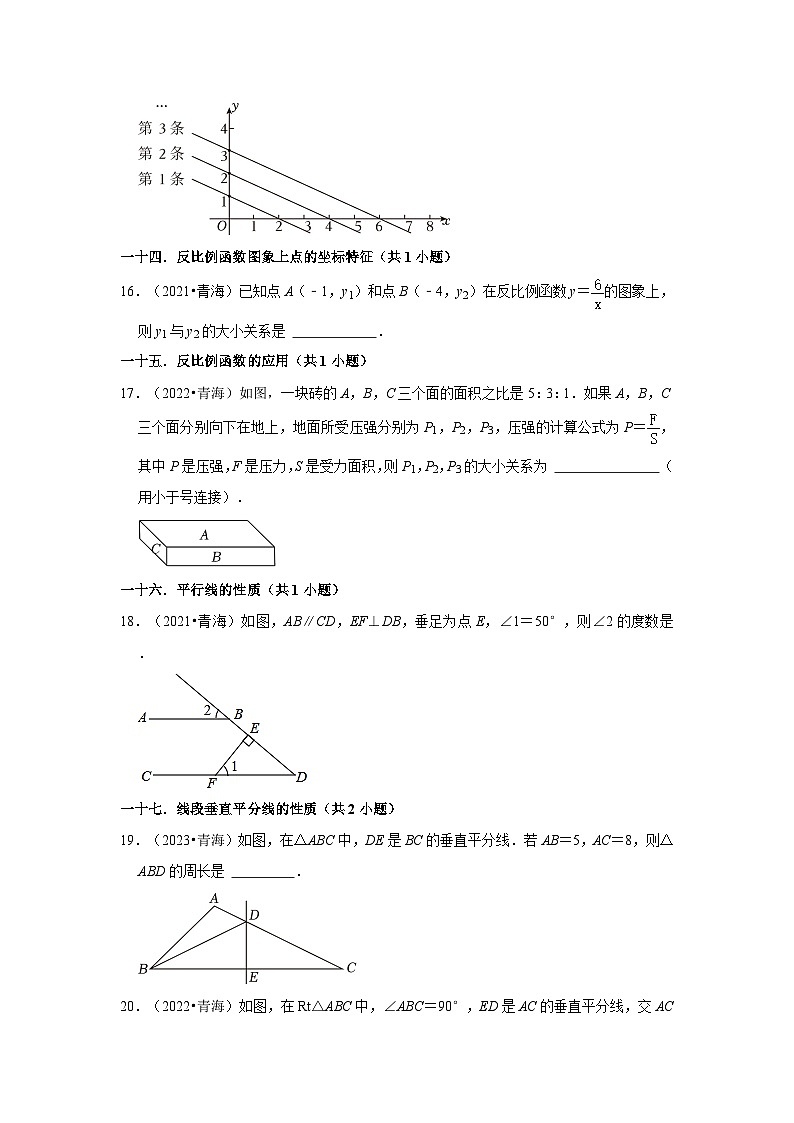
15.(2023•青海)如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是 .
一十四.反比例函数图象上点的坐标特征(共1小题)
16.(2021•青海)已知点A(﹣1,y1)和点B(﹣4,y2)在反比例函数y=的图象上,则y1与y2的大小关系是 .
一十五.反比例函数的应用(共1小题)
17.(2022•青海)如图,一块砖的A,B,C三个面的面积之比是5:3:1.如果A,B,C三个面分别向下在地上,地面所受压强分别为P1,P2,P3,压强的计算公式为P=,其中P是压强,F是压力,S是受力面积,则P1,P2,P3的大小关系为 (用小于号连接).
一十六.平行线的性质(共1小题)
18.(2021•青海)如图,AB∥CD,EF⊥DB,垂足为点E,∠1=50°,则∠2的度数是 .
一十七.线段垂直平分线的性质(共2小题)
19.(2023•青海)如图,在△ABC中,DE是BC的垂直平分线.若AB=5,AC=8,则△ABD的周长是 .
20.(2022•青海)如图,在Rt△ABC中,∠ABC=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=10°,则∠C的度数是 .
一十八.三角形中位线定理(共1小题)
21.(2021•青海)如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,若△DEF的周长为10,则△ABC的周长为 .
一十九.平行四边形的性质(共1小题)
22.(2021•青海)如图,在▱ABCD中,对角线BD=8cm,AE⊥BD,垂足为E,且AE=3cm,BC=4cm,则AD与BC之间的距离为 .
二十.矩形的性质(共1小题)
23.(2022•青海)如图,矩形ABCD的对角线相交于点O,过点O的直线交AD,BC于点E,F,若AB=3,BC=4,则图中阴影部分的面积为 .
二十一.垂径定理(共1小题)
24.(2022•青海)如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是⊙O中弦AB的中点,CD经过圆心O交⊙O于点D,并且AB=4m,CD=6m,则⊙O的半径长为 m.
二十二.点与圆的位置关系(共1小题)
25.(2021•青海)点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是 .
二十三.切线的性质(共1小题)
26.(2023•青海)如图,MN是⊙O的切线,M是切点,连接OM,ON.若∠N=37°,则∠MON的度数是 .
二十四.弧长的计算(共1小题)
27.(2022•青海)如图,从一个腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,则此扇形的弧长为 cm.
二十五.扇形面积的计算(共1小题)
28.(2023•青海)如图,正方形ABCD的边长是4,分别以点A,B,C,D为圆心,2为半径作圆,则图中阴影部分的面积是 (结果保留π).
二十六.轴对称-最短路线问题(共1小题)
29.(2021•青海)如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 .
二十七.坐标与图形变化-平移(共1小题)
30.(2023•青海)在平面直角坐标系中,点(﹣1,2)向右平移3个单位长度得到的点的坐标是 .
二十八.旋转对称图形(共1小题)
31.(2021•青海)如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4cm2,∠AOB为120°,则图中阴影部分的面积之和为 cm2.
二十九.由三视图判断几何体(共1小题)
32.(2022•青海)由若干个相同的小正方体构成的几何体的三视图如图所示,那么构成这个几何体的小正方体的个数是 .
青海省2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一.相反数(共1小题)
1.(2022•青海)﹣2022的相反数是 2022 .
【答案】2022.
【解答】解:﹣2022的相反数是:2022.
故答案为:2022.
二.绝对值(共1小题)
2.(2023•青海)﹣3的绝对值是 3 .
【答案】3.
【解答】解:|﹣3|=3.
故答案为:3.
三.科学记数法—表示较大的数(共3小题)
3.(2023•青海)青藏联网工程东起青海西宁,西至西藏拉萨,被誉为“电力天路”.截至2023年5月“电力天路”已安全运行近12年,累计向西藏送电105.9亿千瓦时,数据105.9亿用科学记数法表示为 1.059×1010 .
【答案】1.059×1010.
【解答】解:105.9亿=10590000000=1.059×1010.
故答案为:1.059×1010.
4.(2022•青海)习近平总书记指出“善于学习,就是善于进步”.“学习强国”平台上线的某天,全国大约有124600000人在平台上学习,将这个数据用科学记数法表示为 1.246×108 .
【答案】1.246×108.
【解答】解:124600000=1.246×108.
故答案为:1.246×108.
5.(2021•青海)5月11日,第七次人口普查结果发布.数据显示,全国人口共14.1178亿人,同2010年第六次全国人口普查数据相比,我国人口10年来继续保持低速增长态势.其中数据“14.1178亿”用科学记数法表示为 1.41178×109 .
【答案】1.41178×109.
【解答】解:14.1178亿
=14.1178×108
=1.41178×109,
故答案为:1.41178×109.
四.算术平方根(共1小题)
6.(2021•青海)观察下列各等式:
①;
②;
③;
…
根据以上规律,请写出第5个等式: 6= .
【答案】6=.
【解答】解:第5个等式,等号左边根号外面是6,被开方数的分子也是6,分母是62﹣1,等号右边是这个整数与这个分数的和的算术平方根,
故答案为:6=.
五.估算无理数的大小(共1小题)
7.(2023•青海)写出一个比﹣大且比小的整数 ﹣1(或0或1) .
【答案】﹣1(或0或1).
【解答】解:∵1<2<4,
∴,
∴﹣2<﹣<﹣1,
∴比﹣大且比小的整数有﹣1,0,1.
故答案为:﹣1(或0或1).
六.同类项(共1小题)
8.(2021•青海)已知单项式2a4b﹣2m+7与3a2mbn+2是同类项,则m+n= 3 .
【答案】3.
【解答】解:根据同类项的定义得:,
∴,
∴m+n=2+1=3,
故答案为:3.
七.规律型:图形的变化类(共1小题)
9.(2022•青海)木材加工厂将一批木料按如图所示的规律依次摆放,则第n个图中共有木料 根.
【答案】.
【解答】解:由图可知:
第一个图形有木料1根,
第二个图形有木料1+2=3(根),
第三个图形有木料1+2+3=6(根),
第四个图形有木料1+2+3+4=10(根),
......
第n个图有木料1+2+3+4+......+n=(根),
故答案为:.
八.二次根式有意义的条件(共1小题)
10.(2022•青海)若式子有意义,则实数x的取值范围是 x>1 .
【答案】x>1.
【解答】解:由题意得x﹣1>0,
解得x>1,
故答案为:x>1.
九.一元二次方程的解(共1小题)
11.(2021•青海)已知m是一元二次方程x2+x﹣6=0的一个根,则代数式m2+m的值等于 6 .
【答案】见试题解答内容
【解答】解:将x=m代入方程x2+x﹣6=0,
得m2+m﹣6=0,
即m2+m=6,
故答案为:6.
一十.由实际问题抽象出一元二次方程(共1小题)
12.(2022•青海)如图,小明同学用一张长11cm,宽7cm的矩形纸板制作一个底面积为21cm2的无盖长方体纸盒,他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计).设剪去的正方形边长为xcm,则可列出关于x的方程为 (11﹣2x)(7﹣2x)=21 .
【答案】(11﹣2x)(7﹣2x)=21.
【解答】解:由题意可得:(11﹣2x)(7﹣2x)=21,
故答案为:(11﹣2x)(7﹣2x)=21.
一十一.解一元一次不等式组(共1小题)
13.(2021•青海)已知点A(2m﹣5,6﹣2m)在第四象限,则m的取值范围是 m>3 .
【答案】m>3.
【解答】解:∵A(2m﹣5,6﹣2m)在第四象限,
∴,
解得m>3,
故答案为:m>3.
一十二.一元一次不等式组的整数解(共1小题)
14.(2022•青海)不等式组的所有整数解的和为 0 .
【答案】0.
【解答】解:,
由①得:x≥﹣2,
由②得x<3,
∴﹣2≤x<3,
x可取的整数有:﹣2,﹣1,0,1,2;
∴所有整数解的和为﹣2﹣1+0+1+2=0,
故答案为:0.
一十三.一次函数图象上点的坐标特征(共1小题)
15.(2023•青海)如图是平面直角坐标系中的一组直线,按此规律推断,第5条直线与x轴交点的横坐标是 10 .
【答案】10.
【解答】解:由题知,这组直线是平行直线,每条直线与x轴交点的横坐标依次是2,4,6...,
∴第5条直线与x轴的交点的横坐标是10.
故答案为:10.
一十四.反比例函数图象上点的坐标特征(共1小题)
16.(2021•青海)已知点A(﹣1,y1)和点B(﹣4,y2)在反比例函数y=的图象上,则y1与y2的大小关系是 y1<y2 .
【答案】y1<y2.
【解答】解:∵反比例函数y=中,k=6>0,
∴此函数在每个象限内,y随x的增大而减小,
∵点A(﹣1,y1)和点B(﹣4,y2)在反比例函数y=的图象上,﹣1>﹣4,
∴y1<y2,
故答案为y1<y2.
一十五.反比例函数的应用(共1小题)
17.(2022•青海)如图,一块砖的A,B,C三个面的面积之比是5:3:1.如果A,B,C三个面分别向下在地上,地面所受压强分别为P1,P2,P3,压强的计算公式为P=,其中P是压强,F是压力,S是受力面积,则P1,P2,P3的大小关系为 P1<P2<P3 (用小于号连接).
【答案】P1<P2<P3.
【解答】解:∵P=,F>0,
∴P随S的增大而减小,
∵A,B,C三个面的面积比是5:3:1,
∴P1,P2,P3的大小关系是:P1<P2<P3,
故答案为:P1<P2<P3.
一十六.平行线的性质(共1小题)
18.(2021•青海)如图,AB∥CD,EF⊥DB,垂足为点E,∠1=50°,则∠2的度数是 40° .
【答案】见试题解答内容
【解答】解:在△DEF中,∠1=50°,∠DEF=90°,
∴∠D=180°﹣∠DEF﹣∠1=40°.
∵AB∥CD,
∴∠2=∠D=40°.
故答案为:40°.
一十七.线段垂直平分线的性质(共2小题)
19.(2023•青海)如图,在△ABC中,DE是BC的垂直平分线.若AB=5,AC=8,则△ABD的周长是 13 .
【答案】13.
【解答】解:∵DE是BC的垂直平分线.
∴BD=CD,
∴AC=AD+CD=AD+BD,
∴△ABD的周长=AB+AD+BD=AB+AC=5+8=13,
故答案为:13.
20.(2022•青海)如图,在Rt△ABC中,∠ABC=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E,∠BAE=10°,则∠C的度数是 40° .
【答案】40°.
【解答】解:∵ED是AC的垂直平分线,
∴AE=EC,
∴∠EAC=∠C,
∵∠ABC=90°,∠BAE=10°,
∴∠EAC+∠C=180°﹣∠BAE﹣∠ABC=80°,
∴∠EAC=∠C=40°,
故答案为:40°.
一十八.三角形中位线定理(共1小题)
21.(2021•青海)如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,若△DEF的周长为10,则△ABC的周长为 20 .
【答案】见试题解答内容
【解答】解:∵点D,E,F分别是△ABC的AB,BC,CA边的中点,
∴EF、DE、DF为△ABC的中位线,
∴EF=AB,DF=BC,DE=AC,
∴AB=2EF,BC=2DF,AC=2DE,
∵△DEF的周长为10,
∴EF+DE+DF=10,
∴2EF+2DE+2DF=20,
∴AB+BC+AC=20,
∴△ABC的周长为20.
故答案为:20.
一十九.平行四边形的性质(共1小题)
22.(2021•青海)如图,在▱ABCD中,对角线BD=8cm,AE⊥BD,垂足为E,且AE=3cm,BC=4cm,则AD与BC之间的距离为 6cm .
【答案】见试题解答内容
【解答】解:
∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
在△ABD和△BCD中
∴△ABD≌△CDB(SSS),
∵AE⊥BD,AE=3cm,BD=8cm,
∴S△ABD=BD•AE=×8×3=12(cm2),
∴S四边形ABCD=2S△ABD=24cm2,
设AD与BC之间的距离为h,
∵BC=4cm,
∴S四边形ABCD=BC•h=4h,
∴4h=24,
解得h=6cm,
故答案为:6cm.
二十.矩形的性质(共1小题)
23.(2022•青海)如图,矩形ABCD的对角线相交于点O,过点O的直线交AD,BC于点E,F,若AB=3,BC=4,则图中阴影部分的面积为 6 .
【答案】6.
【解答】解:∵四边形ABCD是矩形,AB=3,
∴OA=OC,AB=CD=3,AD∥BC,
∴∠AEO=∠CFO;
又∵∠AOE=∠COF,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴S△AOE=S△COF,
∴S阴影=S△AOE+S△BOF+S△COD=S△COF+S△BOF+S△COD=S△BCD,
∵S△BCD=BC•CD==6,
∴S阴影=6.
故答案为6.
二十一.垂径定理(共1小题)
24.(2022•青海)如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是⊙O中弦AB的中点,CD经过圆心O交⊙O于点D,并且AB=4m,CD=6m,则⊙O的半径长为 m.
【答案】.
【解答】解:连接OA,如图,设⊙O的半径为rm,
∵C是⊙O中弦AB的中点,CD过圆心,
∴CD⊥AB,AC=BC=AB=2m,
在Rt△AOC中,∵OA=rm,OC=(6﹣r)m,
∴22+(6﹣r)2=r2,
解得r=,
即⊙O的半径长为m.
故答案为:.
二十二.点与圆的位置关系(共1小题)
25.(2021•青海)点P是非圆上一点,若点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的半径是 6.5cm或2.5cm .
【答案】6.5cm或2.5cm.
【解答】解:分为两种情况:
①当点在圆内时,如图1,
∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,
∴直径AB=4+9=13(cm),
∴半径r=6.5cm;
②当点在圆外时,如图2,
∵点到圆上的最小距离PB=4cm,最大距离PA=9cm,
∴直径AB=9﹣4=5(cm),
∴半径r=2.5cm.
综上所述,圆O的半径为6.5cm或2.5cm.
故答案为:6.5cm或2.5cm.
二十三.切线的性质(共1小题)
26.(2023•青海)如图,MN是⊙O的切线,M是切点,连接OM,ON.若∠N=37°,则∠MON的度数是 53° .
【答案】53°.
【解答】解:∵MN是⊙O的切线,M是切点,
∴∠OMN=90°,
∵∠N=37°,
∴∠MON=90°﹣∠N=53°,
故答案为:53°.
二十四.弧长的计算(共1小题)
27.(2022•青海)如图,从一个腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,则此扇形的弧长为 20π cm.
【答案】20π.
【解答】解:过O作OE⊥AB于E,当扇形的半径为OE时扇形OCD最大,
∵OA=OB=60cm,∠AOB=120°,
∴∠A=∠B=30°,
∴OE=OA=30cm,
∴弧CD的长==20πcm,
故答案为:20π.
二十五.扇形面积的计算(共1小题)
28.(2023•青海)如图,正方形ABCD的边长是4,分别以点A,B,C,D为圆心,2为半径作圆,则图中阴影部分的面积是 16﹣4π (结果保留π).
【答案】16﹣4π.
【解答】解:由图得,阴影面积=正方形面积﹣4扇形面积,
即阴影面积=正方形面积﹣圆的面积,
∴S阴影=42﹣π•22=16﹣4π.
故答案为:16﹣4π.
二十六.轴对称-最短路线问题(共1小题)
29.(2021•青海)如图,正方形ABCD的边长为8,点M在DC上且DM=2,N是AC上的一动点,则DN+MN的最小值是 10 .
【答案】见试题解答内容
【解答】解:∵正方形是轴对称图形,点B与点D是关于直线AC为对称轴的对称点,
∴连接BN,BD,
∴BN=ND,
∴DN+MN=BN+MN,
连接BM交AC于点P,
∵点 N为AC上的动点,
由三角形两边和大于第三边,
知当点N运动到点P时,
BN+MN=BP+PM=BM,
BN+MN的最小值为BM的长度,
∵四边形ABCD为正方形,
∴BC=CD=8,CM=8﹣2=6,∠BCM=90°,
∴BM==10,
∴DN+MN的最小值是10.
故答案为:10.
二十七.坐标与图形变化-平移(共1小题)
30.(2023•青海)在平面直角坐标系中,点(﹣1,2)向右平移3个单位长度得到的点的坐标是 (2,2) .
【答案】(2,2).
【解答】解:点(﹣1,2)向右平移3个单位长度得到的点的坐标是(﹣1+3,2),即(2,2).
故答案为:(2,2).
二十八.旋转对称图形(共1小题)
31.(2021•青海)如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4cm2,∠AOB为120°,则图中阴影部分的面积之和为 4 cm2.
【答案】见试题解答内容
【解答】解:∵三个叶片组成,绕点O旋转120°后可以和自身重合,
而∠AOB为120°,
∴图中阴影部分的面积之和=(4+4+4)=4(cm2).
故答案为4.
二十九.由三视图判断几何体(共1小题)
32.(2022•青海)由若干个相同的小正方体构成的几何体的三视图如图所示,那么构成这个几何体的小正方体的个数是 5 .
【答案】5.
【解答】解:由三视图可得,构成这个几何体的小正方体的个数是:1+2+1+1=5.如图:
故答案为:5.
相关试卷
这是一份河南省2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共16页。
这是一份陕西省2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共19页。试卷主要包含了计算,分解因式等内容,欢迎下载使用。
这是一份山西省2021-2023三年中考数学真题分类汇编-02填空题知识点分类,共15页。试卷主要包含了计算等内容,欢迎下载使用。









