山东省菏泽市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（较难题）

这是一份山东省菏泽市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（较难题），共36页。试卷主要包含了计算，，OA＝，tan∠AOC＝，，与y轴交于点C，两点，直线x＝3与x轴交于点C等内容，欢迎下载使用。
山东省菏泽市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（较难题）
一．实数的运算（共1小题）
1．（2023•巨野县二模）计算：．
二．分式方程的应用（共1小题）
2．（2023•曹县二模）在全民健身运动中，骑行运动颇受人民青睐．甲、乙两骑行爱好者约定从A地沿相同路线骑行去距离30千米的B地，已知甲骑行的平均速度是乙骑行平均速度的1.2倍，若乙先骑行20分钟，然后甲从A地出发，则甲、乙恰好同时到达B地，求甲骑行的平均速度是每分钟多少千米？
三．一次函数的应用（共1小题）
3．（2023•单县二模）某地为响应政府号召，芦笋种植户借助电商平台，在线下批发的基础上同步在电商平台上零售芦笋．已知线上零售40kg，线下批发80kg芦笋共获得4000元；线上零售60kg和线下批发80kg芦笋销售额相同．
（1）求线上零售和线下批发芦笋的单价分别是每千克多少元？
（2）该产地某种植大户某月线上零售和线下批发共销售芦笋2000kg，设线上零售mkg，获得的总销售额为w元；
①请写出w与m的函数关系式；
②若总销售额不低于70000元，则线上零售量至少应达到多少千克？
四．反比例函数与一次函数的交点问题（共1小题）
4．（2023•曹县二模）如图，直线y＝k1x+b与反比例函数y＝的图象相交于点A，B，直线AB与x轴交于点C，与y轴交于点D（0，﹣2），OA＝，tan∠AOC＝．
（1）求直线AB与反比例函数的表达式；
（2）若点P是第四象限内反比例函数图象上一点，S△OCP＝，求点P的坐标．

五．反比例函数综合题（共1小题）
5．（2023•菏泽二模）如图，一次函数y1＝k1x+4与反比例函数y2＝的图象交于点A（2，m）和B（﹣6，﹣2），与y轴交于点C．
（1）求一次函数与反比例函数的表达式；
（2）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点，设直线OP与线段AD交于点E，当S四边形ODAC：S△ODE＝5：1时，求点P的坐标；
（3）在（2）的条件下，点M是直线OP上的一个动点，当△MBC是以BC为斜边的直角三角形时，求点M的坐标．

六．二次函数综合题（共2小题）
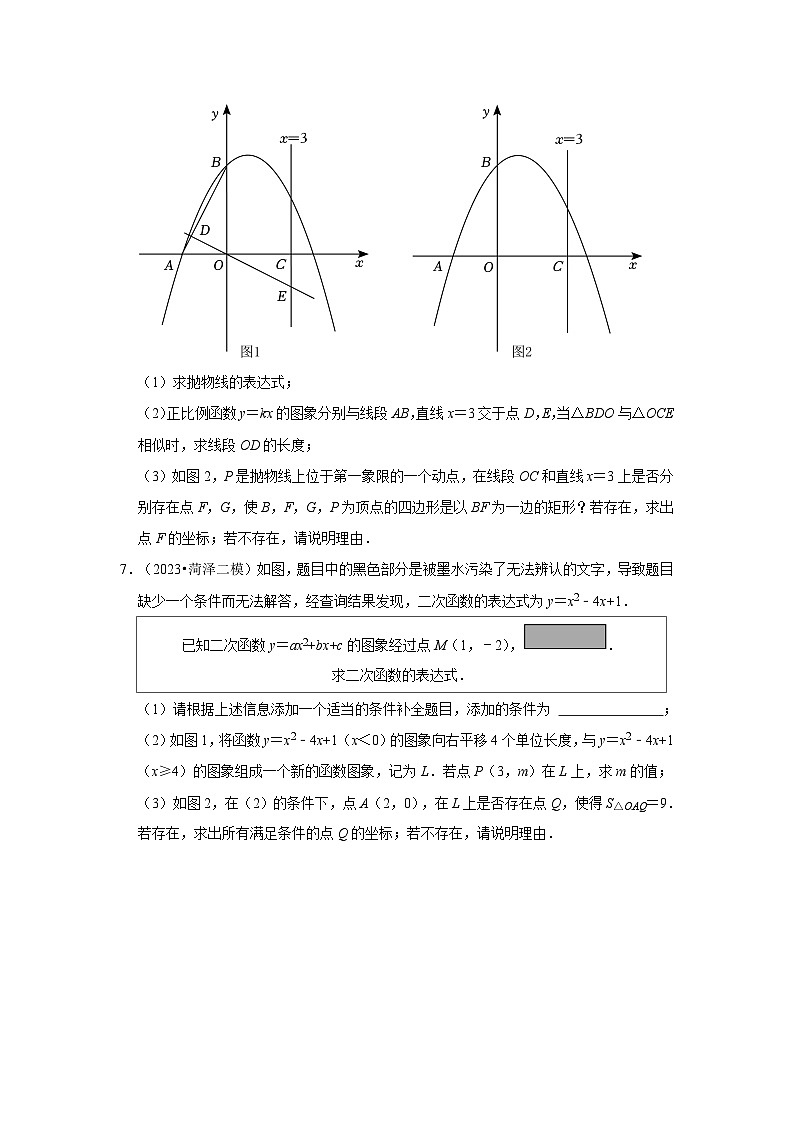
6．（2023•定陶区二模）如图1，在平面直角坐标系xOy中，已知抛物线经过A（﹣2，0），B（0，4）两点，直线x＝3与x轴交于点C．

（1）求抛物线的表达式；
（2）正比例函数y＝kx的图象分别与线段AB，直线x＝3交于点D，E，当△BDO与△OCE相似时，求线段OD的长度；
（3）如图2，P是抛物线上位于第一象限的一个动点，在线段OC和直线x＝3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．
7．（2023•菏泽二模）如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少一个条件而无法解答，经查询结果发现，二次函数的表达式为y＝x2﹣4x+1．
已知二次函数y＝ax2+bx+c的图象经过点M（1，﹣2），．
求二次函数的表达式．
（1）请根据上述信息添加一个适当的条件补全题目，添加的条件为 　 　；
（2）如图1，将函数y＝x2﹣4x+1（x＜0）的图象向右平移4个单位长度，与y＝x2﹣4x+1（x≥4）的图象组成一个新的函数图象，记为L．若点P（3，m）在L上，求m的值；
（3）如图2，在（2）的条件下，点A（2，0），在L上是否存在点Q，使得S△OAQ＝9．若存在，求出所有满足条件的点Q的坐标；若不存在，请说明理由．

七．菱形的性质（共1小题）
8．（2023•巨野县二模）如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD上的点，过点A作AF∥BC交BE的延长线于点F，若四边形ADCF是菱形，求证：BE＝FE．

八．矩形的性质（共1小题）
9．（2023•定陶区二模）矩形ABCD和矩形AECF有公共顶点A和C，AE、BC相交于点G，AD、CF相交于点H．求证：△ABG≌△CDH．

九．正方形的性质（共1小题）
10．（2023•菏泽二模）如图，在正方形ABCD中，点P是对角线AC上一动点，PM⊥AB，PN⊥BC，垂足分别为点M，N，连接DP并延长，交MN于点E．
小亮说：点P在运动过程中，PD与MN的数量关系为PD＝MN；
小莹说：点P在运动过程中，PD与MN的位置关系为PD⊥MN．
小亮和小莹两人的发现，　 　是对的；（填“小亮”“小莹”“两人都”）并说明你的理由．

一十．四边形综合题（共1小题）
11．（2023•菏泽二模）综合与实践
问题情境：数学活动课上，老师出示了一个问题：如图①，在平行四边形ABCD中，BE⊥AD，垂足为E，F为CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明．

（1）独立思考：请解答老师提出的问题；
（2）实践探究：希望小组受此问题的启发，将平行四边形ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C'，连接DC'并延长交AB于点G，请判断AG与BG的数量关系，并加以证明．
（3）问题解决：智慧小组突发奇想，将平行四边形ABCD沿过点B的直线折叠，如图③，点A的对应点为A'，使A'B⊥CD于点H，折痕交AD于点M，连接A'M，交CD于点N．该小组提出一个问题：若此平行四边形ABCD的面积为20，边长AB＝5，，求图中阴影部分（四边形BHNM）的面积．请你思考此问题，直接写出结果．
一十一．切线的性质（共2小题）
12．（2023•定陶区二模）如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F．
（1）求证：AB＝CB；
（2）若AB＝18，sinA＝，求BF的长．

13．（2023•菏泽二模）如图，在Rt△ABC中，∠C＝90°，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知AD是⊙O的切线．
（1）求证：∠CAD＝∠B．
（2）若BC＝8，AC＝4，求⊙O的半径．

一十二．切线的判定与性质（共1小题）
14．（2023•鄄城县二模）如图，已知AB是⊙O的直径，点C，E在⊙O上，点D是AB延长线上一点，且∠BCD＝∠BEC．
（1）求证：DC是⊙O的切线；
（2）若BD＝4，CD＝6，求∠D的正切值．
​

一十三．解直角三角形的应用-仰角俯角问题（共2小题）
15．（2023•定陶区二模）如图，某电影院的观众席成“阶梯状”，每一级台阶的水平宽度都为1m，垂直高度都为0.3m．测得在C点的仰角∠ACE＝42°，测得在D点的仰角∠ADF＝35°．求银幕AB的高度．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.7，sin42°≈0.67，cos42°≈0.74，tan42°≈0.9）

16．（2023•菏泽二模）某校“综合与实践”活动小组的同学要测量AB，CD两座楼之间的距离，设计了如下测量方案：无人机在AB，CD两楼之间上方的点O处，点O距地面AC的高度为60m，此时观测到楼AB底部点A处的俯角为70°，楼CD上点E处的俯角为30°，沿水平方向由点O飞行24m到达点F，测得点E处俯角为60°，其中点A，B，C，D，E，F，O均在同一竖直平面内．请根据以上数据求：
（1）无人机在O处时到楼AB的水平距离；
（2）楼AB与CD之间的距离．（结果均精确到1m，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

一十四．解直角三角形的应用-方向角问题（共1小题）
17．（2023•单县二模）如图，海中有一小岛A，今有一货轮由南向北航行，开始在A岛西南方向的B处，往北行驶30海里后到达该岛南偏西76°的C处．之后，货轮继续向北航行．一艘快艇从A岛出发，沿北偏西37°方向行驶，恰好在D处与货轮相遇，求相遇时快艇行驶的距离AD．（结果保留整数，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin76°≈0.97，cos76°≈0.24，tan76°≈4.00）

一十五．列表法与树状图法（共1小题）
18．（2023•鄄城县二模）（微信圈有篇热传的文章《如果想毁掉一个孩子，就给他一部手机！》，2021年教育部办公厅下发关于加强中小学生手机管理工作的通知，通知中提到：有限带入校园，细化管理措施，加强教育引导，做好家校沟通，强化督促检查五点学校管理措施，为了解学生手机使用情况，某学校组织开展了“手机伴我健康行”的主题活动，学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，图②的统计图，已知“查资料”的人数是40人．
​
（1）在这次调查中，一共抽取了 　 　名学生；
（2）在扇形统计图中，“玩游戏”对应的圆心角的度数是 　 　度；
（3）补全条形统计图；
（4）在使用手机“查资料”的学生中，恰有3人每周都是使用手机50分钟，其中2女1男，计划在这3个学生中随机抽选两个到全年级分享手机管理使用经验，请用列表或画树状图的方法求所选两个学生中有一个男生的概率．

山东省菏泽市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（较难题）
参考答案与试题解析
一．实数的运算（共1小题）
1．（2023•巨野县二模）计算：．
【答案】﹣1．
【解答】解：原式＝
＝﹣1．
二．分式方程的应用（共1小题）
2．（2023•曹县二模）在全民健身运动中，骑行运动颇受人民青睐．甲、乙两骑行爱好者约定从A地沿相同路线骑行去距离30千米的B地，已知甲骑行的平均速度是乙骑行平均速度的1.2倍，若乙先骑行20分钟，然后甲从A地出发，则甲、乙恰好同时到达B地，求甲骑行的平均速度是每分钟多少千米？
【答案】甲骑行的平均速度是每分钟0.3千米．
【解答】解：设乙骑行的平均速度是每分钟x千米，则甲骑行的平均速度是每分钟1.2x千米，
由题意得：﹣＝20，
解得：x＝0.25，
经检验，x＝0.25是原方程的解，且符合题意，
∴1.2x＝1.2×0.25＝0.3，
答：甲骑行的平均速度是每分钟0.3千米．
三．一次函数的应用（共1小题）
3．（2023•单县二模）某地为响应政府号召，芦笋种植户借助电商平台，在线下批发的基础上同步在电商平台上零售芦笋．已知线上零售40kg，线下批发80kg芦笋共获得4000元；线上零售60kg和线下批发80kg芦笋销售额相同．
（1）求线上零售和线下批发芦笋的单价分别是每千克多少元？
（2）该产地某种植大户某月线上零售和线下批发共销售芦笋2000kg，设线上零售mkg，获得的总销售额为w元；
①请写出w与m的函数关系式；
②若总销售额不低于70000元，则线上零售量至少应达到多少千克？
【答案】（1）线上零售芦笋的单价为每千克40元，线下批发芦笋的单价为每千克30元；
（2）线上零售量至少应达到1000千克．
【解答】解：（1）设线上零售芦笋的单价为每千克x元，线下批发芦笋的单价为每千克y元，
由题意得，，
解得，
答：线上零售芦笋的单价为每千克40元，线下批发芦笋的单价为每千克30元；
（2）①由题意得，
w＝40m+30（2000﹣m）＝10m+60000，
即w与m的函数关系式为w＝10m+60000；
②由题意可得：10m+60000≥70000，
解得m≥1000，
答：线上零售量至少应达到1000千克．
四．反比例函数与一次函数的交点问题（共1小题）
4．（2023•曹县二模）如图，直线y＝k1x+b与反比例函数y＝的图象相交于点A，B，直线AB与x轴交于点C，与y轴交于点D（0，﹣2），OA＝，tan∠AOC＝．
（1）求直线AB与反比例函数的表达式；
（2）若点P是第四象限内反比例函数图象上一点，S△OCP＝，求点P的坐标．

【答案】（1）反比例函数解析式为，直线AB的解析式为；
（2）P（1，﹣2）．
【解答】解：（1）过点A作AE⊥x轴于点E，则，
设AE＝x，则OE＝2x，
根据勾股定理得，AE2+OE2＝OA2，
∴，
∴x＝1（负数舍去），
∴AE＝1，OE＝2，
∴点A的坐标为（﹣2，1），
∵点A在反比例函数y＝的图象上，
∴k2＝﹣2×1＝﹣2，
∴反比例函数解析式为，
由直线y＝k1x+b经过点A，D得，
解得，
∴直线AB的解析式为；
（2）由，得，
∴，
设点P的纵坐标为y，
∵S△OCP＝，
∴，
解得y＝﹣2，
∴横坐标为：，
∴点P的坐标为（1，﹣2）．

五．反比例函数综合题（共1小题）
5．（2023•菏泽二模）如图，一次函数y1＝k1x+4与反比例函数y2＝的图象交于点A（2，m）和B（﹣6，﹣2），与y轴交于点C．
（1）求一次函数与反比例函数的表达式；
（2）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点，设直线OP与线段AD交于点E，当S四边形ODAC：S△ODE＝5：1时，求点P的坐标；
（3）在（2）的条件下，点M是直线OP上的一个动点，当△MBC是以BC为斜边的直角三角形时，求点M的坐标．

【答案】（1）一次函数y＝x+4，反比例函数y＝；
（2）P（2，2）；
（3）M（﹣1+，﹣1+）或M（﹣1﹣，﹣1﹣）．
【解答】解：（1）将点A（2，m）和B（﹣6，﹣2）代入y2＝得，
k2＝12，m＝6，
∴A（2，6），反比例函数y＝，
将点A（2，6）代入y1＝k1x+4得，
2k1+4＝6，
∴k1＝1，
∴一次函数y＝x+4；
（2）如图，一次函数y＝x+4中，当x＝0时，y＝4，
∴C（0，4），
∴OC＝4，

∵S四边形ODAC：S△ODE＝5：1，
∴（4+6）×2＝5××2×DE，
解得DE＝2，
∴E（2，2），
∴直线OP的解析式为y＝x，
∴＝x，
∵x＞0，
∴x＝2，
∴P（2，2）；
（3）如图，取BC的中点G，连接MG，

∵∠BMC＝90°，
∴GM＝BC，
∵B（﹣6，﹣2），C（0，4），
∴点G（﹣3，1），
∴GC＝，
∴GM＝3，
设M（x，x），
∴（x+3）2+（x﹣1）2＝18，
解得x1＝﹣1+，x2＝﹣1﹣，
∴M（﹣1+，﹣1+）或M（﹣1﹣，﹣1﹣）．
六．二次函数综合题（共2小题）
6．（2023•定陶区二模）如图1，在平面直角坐标系xOy中，已知抛物线经过A（﹣2，0），B（0，4）两点，直线x＝3与x轴交于点C．

（1）求抛物线的表达式；
（2）正比例函数y＝kx的图象分别与线段AB，直线x＝3交于点D，E，当△BDO与△OCE相似时，求线段OD的长度；
（3）如图2，P是抛物线上位于第一象限的一个动点，在线段OC和直线x＝3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．
【答案】（1）y＝﹣x2+x+4；
（2）；
（3）存在，点F的坐标为（2，0）或（，0）．
【解答】解：（1）把A（﹣2，0），B（0，4）两点代入抛物线表达式得：
，
解得：，
则抛物线的表达式为：y＝﹣x2+x+4；

（2）由题意得，当△BDO与△OCE相似时，只有∠BDO＝90°，
在Rt△ADO中，tan∠DAO＝＝2，
则sin∠DAO＝＝，
则DO＝OAsin∠DAO＝2×＝；

（3）存在，
B，F，G，P为顶点的四边形是以BF为一边的矩形有两种情况：
设P（t，﹣t2+t+4），
①如图1，过点P作PH⊥y轴于H，

∵四边形BPGF是矩形，
∴BP＝FG，∠PBF＝∠BFG＝90°，
∴∠CFG+∠BFO＝∠BFO+∠OBF＝∠CFG+∠CGF＝∠OBF+∠PBH＝90°，
∴∠PBH＝∠OFB＝∠CGF，
∵∠PHB＝∠FCG＝90°，
∴△PHB≌△FCG（AAS），
∴PH＝CF，
∴CF＝PH＝t，OF＝3﹣t，
∵∠PBH＝∠OFB，
∴，即，
解得：t1＝0（舍），t2＝1，
∴F（2，0）；
②如图2，过点G作GN⊥y轴于N，过点P作PM⊥x轴于M，

同①可得：NG＝FM＝3，OF＝t﹣3，
∵∠OFB＝∠FPM，
∴tan∠OFB＝tan∠FPM，
∴，即，
解得：t＝或（舍），
∴F（，0）；
综上，点F的坐标为（2，0）或（，0）．
7．（2023•菏泽二模）如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少一个条件而无法解答，经查询结果发现，二次函数的表达式为y＝x2﹣4x+1．
已知二次函数y＝ax2+bx+c的图象经过点M（1，﹣2），．
求二次函数的表达式．
（1）请根据上述信息添加一个适当的条件补全题目，添加的条件为 　顶点（2，﹣3）　；
（2）如图1，将函数y＝x2﹣4x+1（x＜0）的图象向右平移4个单位长度，与y＝x2﹣4x+1（x≥4）的图象组成一个新的函数图象，记为L．若点P（3，m）在L上，求m的值；
（3）如图2，在（2）的条件下，点A（2，0），在L上是否存在点Q，使得S△OAQ＝9．若存在，求出所有满足条件的点Q的坐标；若不存在，请说明理由．

【答案】（1）顶点（2，﹣3）；（2）m＝6；（3）存在，Q点坐标为：（6﹣2，9）或（2+2，9）．
【解答】解：（1）∵y＝x2﹣4x+1＝（x﹣2）2﹣3，
故可以添加的条件为：顶点（2，﹣3），
故答案为：顶点（2，﹣3）；

（2）∵y＝x2﹣4x+1＝（x﹣2）2﹣3，
则平移后的表达式为：y＝（x﹣6）2﹣3，
当x＝3时，y＝（x﹣6）2﹣3＝6，
则m＝6；

（3）存在点Q，理由：
当Q点在抛物线y＝（x﹣6）2﹣3的部分上时，设Q（t，t2﹣12t+33），
∴S△OAQ＝×2×（t2﹣12t+33）＝9，
解得t＝6，
∵t＜4，
∴则t＝6﹣2，
∴Q（6﹣2，9）；
当Q点在抛物线y＝x2﹣4x+1的部分上时，设Q（m，m2﹣4m+1），
∴S△OAQ＝2×（m2﹣4m+1）＝9，
解得m＝2±2，
∵m≥4，
∴m＝2+2，
∴Q（2+2，9）；
综上所述：Q点坐标为：（6﹣2，9）或（2+2，9）．
七．菱形的性质（共1小题）
8．（2023•巨野县二模）如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD上的点，过点A作AF∥BC交BE的延长线于点F，若四边形ADCF是菱形，求证：BE＝FE．

【答案】见解析．
【解答】证明：∵∠BAC＝90°，D是BC的中点，
∴AD＝BD＝BC，
∵四边形ADCF是菱形，
∴AD＝AF，
∴BD＝AF，
方法一：
∵AF∥BC，
∴∠AFE＝∠DBE，∠FAE＝∠BDE．
在△AFE和△DBE中，
，
∴△AFE≌△DBE（ASA），
∴BE＝FE．
方法二：连接DF，
∵AF∥BC，
∴四边形ABDF是平行四边形．
∵点E是平行四边形ABDF对角线AD、BF的交点，
∴BE＝FE．

八．矩形的性质（共1小题）
9．（2023•定陶区二模）矩形ABCD和矩形AECF有公共顶点A和C，AE、BC相交于点G，AD、CF相交于点H．求证：△ABG≌△CDH．

【答案】证明过程见解答．
【解答】证明：∵四边形ABCD与四边形AECF都是矩形，
∴AH∥GC，AG∥CH，
∴四边形AGCH是平行四边形，
∴∠GAH＝∠GCH，
∵四边形ABCD与四边形AECF都是矩形，
∴∠B＝∠D＝90°，∠BAD＝∠BCD＝90°，AB＝CD，
∴∠BAG＝90°﹣∠GAH，∠DCH＝90°﹣∠GCH，
∴∠BAG＝∠DCH，
在△ABG与△CDH中，
，
∴△ABG≌△CDH（SAS）．
九．正方形的性质（共1小题）
10．（2023•菏泽二模）如图，在正方形ABCD中，点P是对角线AC上一动点，PM⊥AB，PN⊥BC，垂足分别为点M，N，连接DP并延长，交MN于点E．
小亮说：点P在运动过程中，PD与MN的数量关系为PD＝MN；
小莹说：点P在运动过程中，PD与MN的位置关系为PD⊥MN．
小亮和小莹两人的发现，　两人都对　是对的；（填“小亮”“小莹”“两人都”）并说明你的理由．

【答案】两人都对．
【解答】解：两人都对；
延长NP，交AD于点F，则四边形AMPF为正方形，
∵四边形ABCD是正方形，
∴∠ABC＝90°，AB＝AD，
∵PM⊥AB，PN⊥BC，
∴∠PMB＝90°，∠PNB＝90°，
∴四边形PNBM是矩形，
∴PN＝MB，∠MPN＝90°，
∵四边形AMPF是正方形，
∴AM＝AF＝PM＝PF，∠PFA＝90°，
∵AB＝AD，
∴MB＝FD，
∵PN＝MB，
∴PN＝FD，
又∵PM＝PF，∠PFD＝∠MPN＝90°，
在△MPN与△PFD中，
，
∴△MPN≌△PFD（SAS），
∴PD＝MN，
∵△MPN≌△PFD，
∴∠PNM＝∠FDP，
∵∠NPE＝∠FPD，
∴∠NPE+∠PNM＝∠FPD+∠FDP＝90°，
∴∠PEN＝90°，
∴PD⊥MN．
故答案为：两人都对．

一十．四边形综合题（共1小题）
11．（2023•菏泽二模）综合与实践
问题情境：数学活动课上，老师出示了一个问题：如图①，在平行四边形ABCD中，BE⊥AD，垂足为E，F为CD的中点，连接EF，BF，试猜想EF与BF的数量关系，并加以证明．

（1）独立思考：请解答老师提出的问题；
（2）实践探究：希望小组受此问题的启发，将平行四边形ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C'，连接DC'并延长交AB于点G，请判断AG与BG的数量关系，并加以证明．
（3）问题解决：智慧小组突发奇想，将平行四边形ABCD沿过点B的直线折叠，如图③，点A的对应点为A'，使A'B⊥CD于点H，折痕交AD于点M，连接A'M，交CD于点N．该小组提出一个问题：若此平行四边形ABCD的面积为20，边长AB＝5，，求图中阴影部分（四边形BHNM）的面积．请你思考此问题，直接写出结果．
【答案】（1）EF＝BF，证明见解答；
（2）AG＝BG，证明见解答；
（3）．
【解答】解：（1）EF＝BF，
证明：如图，作FH∥AD交BE于H，

∵四边形ABCD是平行四边形，
∴AD∥BC，
∵FH∥AD，
∴DE∥FH∥CB，
∵DF＝CF，
∴，
∴EH＝HB，
∵BE⊥AD，FH∥AD，
∴FH⊥EB，
∴EF＝BF；
（2）AG＝BG，
证明：如图，连接CC'，

∵△BFC'是由△BFC翻折得到，
∴BF⊥CC'，FC＝FC'，
∵DF＝FC，
∴DF＝FC＝FC'，
∴∠CC'D＝90°，
∴CC'⊥GD，
∴DG∥BF，
∵DF∥BG，
∴四边形DFBG是平行四边形，
∴DF＝BG，
∵AB＝CD，，
∴，
∴AG＝GB；
（3）如图，过点D作DJ⊥AB于点J，过点M作MT⊥AB于T，

∵S平行四边形ABCD＝AB•DJ，
∴，
∵四边形ABCD是平行四边形，
∴，AB∥CD，
∴，
∵A'B⊥AB，DJ⊥AB，
∴∠DJB＝∠JBH＝∠DHB＝90°，
∴四边形DJBH为矩形，
∴BH＝DJ＝4，
∴A'H＝A'B﹣BH＝5﹣4＝1，
∵，
设AT＝x，则MT＝2x，
∵∠ABM＝∠MBA'＝45°，
∴MT＝TB＝2x，
∴3x＝5，
∴，
∴，
∵，
∴NH＝2，
∴，
∴．
一十一．切线的性质（共2小题）
12．（2023•定陶区二模）如图，D是以AB为直径的⊙O上一点，过点D的切线DE交AB的延长线于点E，过点B作BC⊥DE交AD的延长线于点C，垂足为点F．
（1）求证：AB＝CB；
（2）若AB＝18，sinA＝，求BF的长．

【答案】（1）证明见解析；（2）2．
【解答】（1）证明：连接OD，
∵DE切⊙O于D，
∴OD⊥DE，
∵BC⊥DE，
∴OD∥BC，
∴∠C＝∠ODA，
∵OD＝OA，
∴∠A＝∠ODA，
∴∠A＝∠C，
∴AB＝CB；
（2）解：连接BD，
∵AB是圆的直径，
∴∠ADB＝90°，
∴∠BDC＝180°﹣∠ADB＝90°，
∵sinA＝＝，AB＝18，
∴BD＝6，
∵∠BDF+∠CDF＝∠C+∠CDF＝90°，
∴∠BDF＝∠C，
∵∠A＝∠C，
∴∠BDF＝∠A，
∴sin∠BDF＝sinA＝，
∴＝，
∴BF＝6×＝2．

13．（2023•菏泽二模）如图，在Rt△ABC中，∠C＝90°，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD．已知AD是⊙O的切线．
（1）求证：∠CAD＝∠B．
（2）若BC＝8，AC＝4，求⊙O的半径．

【答案】（1）见解析；
（2）⊙O的半径为．
【解答】（1）证明：连接OD，

∵OB＝OD，
∴∠3＝∠B，
∵AD为圆O的切线，
∴∠4＝90°，
∴∠2+∠3＝90°，
∵∠C＝90°，
∴∠1+∠2＝90°，
∴∠1＝∠3，
∴∠CAD＝∠B；
（2）解：在Rt△ABC中，BC＝8，AC＝4，
∴AB＝＝＝4，
∵∠CAD＝∠B，∠ACD＝∠BCA，
∴△ACD∽△BCA，
∴＝，
∴＝，
∴AD＝2，
在Rt△ADO中，AD2+OD2＝AO2，
设OD＝r，则AO＝4﹣r，
∴（2）2+r2＝（4﹣r）2，
解得：r＝，
即⊙O的半径为．
一十二．切线的判定与性质（共1小题）
14．（2023•鄄城县二模）如图，已知AB是⊙O的直径，点C，E在⊙O上，点D是AB延长线上一点，且∠BCD＝∠BEC．
（1）求证：DC是⊙O的切线；
（2）若BD＝4，CD＝6，求∠D的正切值．
​

【答案】（1）见解答；
（2）．
【解答】（1）证明：作直径CF，连接BF，如图，
∵AB是⊙O的直径，
∴∠CBF＝90°，
∴∠F+∠BCF＝90°，
∵∠F＝∠BEC，∠BEC＝∠BCD，
∴∠BCD+∠BCF＝90°，
即∠DCF＝90°，
∴CF⊥CD，
∵CF为直径，
∴DC是⊙O的切线；
（2）解：设⊙O的半径为r，则OB＝OC＝r，OD＝r+4，
在Rt△OCD中，r2+62＝（r+4）2，
解得r＝，
即OC＝，
∴tanD＝＝＝，
即∠D的正切值为．

一十三．解直角三角形的应用-仰角俯角问题（共2小题）
15．（2023•定陶区二模）如图，某电影院的观众席成“阶梯状”，每一级台阶的水平宽度都为1m，垂直高度都为0.3m．测得在C点的仰角∠ACE＝42°，测得在D点的仰角∠ADF＝35°．求银幕AB的高度．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.7，sin42°≈0.67，cos42°≈0.74，tan42°≈0.9）

【答案】5.1m．
【解答】解：延长CE、DF交AB于H、G，
由题意知，∠AGD＝∠AHC＝90°，
在Rt△AGD中，∠ADG＝35°，
∴tan35°＝，
即DG＝，
在Rt△ACH中，∠ACH＝42°，
∴tan42°＝，
即CH＝，
∵AH＝AG+GH，GH＝0.3，
∴CH＝，
∵DG﹣CH＝1，
∴﹣＝1，
∴﹣＝1
解得：AG＝4.2，
∴AB＝AG+GH+BH＝4.2+0.3+0.6＝5.1．
答：银幕AB的高度约为5.1m．

16．（2023•菏泽二模）某校“综合与实践”活动小组的同学要测量AB，CD两座楼之间的距离，设计了如下测量方案：无人机在AB，CD两楼之间上方的点O处，点O距地面AC的高度为60m，此时观测到楼AB底部点A处的俯角为70°，楼CD上点E处的俯角为30°，沿水平方向由点O飞行24m到达点F，测得点E处俯角为60°，其中点A，B，C，D，E，F，O均在同一竖直平面内．请根据以上数据求：
（1）无人机在O处时到楼AB的水平距离；
（2）楼AB与CD之间的距离．（结果均精确到1m，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

【答案】（1）22m；
（2）58m．
【解答】解：（1）延长AB，CD分别与直线OF交于点G和点H，

则AG＝60m，GH＝AC，∠AGO＝∠EHO＝90°，
在Rt△AGO中，∠AOG＝70°，
∴，
∴无人机在O处时到楼AB的水平距离为22m．
（2）∵∠HFE是△OFE的一个外角，
∴∠OEF＝∠HFE﹣∠FOE＝30°，
∴∠FOE＝∠OEF＝30°，
∴OF＝EF＝24m，
在Rt△EFH中，∠HFE＝60°，
∴FH＝EF•cos60°＝24×＝12（m），
∴AC＝GH＝OG+OF+FH＝22+24+12＝58（m），
∴楼AB与CD之间的距离AC的长约为58m．
一十四．解直角三角形的应用-方向角问题（共1小题）
17．（2023•单县二模）如图，海中有一小岛A，今有一货轮由南向北航行，开始在A岛西南方向的B处，往北行驶30海里后到达该岛南偏西76°的C处．之后，货轮继续向北航行．一艘快艇从A岛出发，沿北偏西37°方向行驶，恰好在D处与货轮相遇，求相遇时快艇行驶的距离AD．（结果保留整数，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin76°≈0.97，cos76°≈0.24，tan76°≈4.00）

【答案】相遇时快艇行驶的距离AD为67海里．
【解答】解：FE是过A南北方向的直线，过D作DE⊥EF于E，过B作BF⊥EF于F，过A作AH⊥BD于H，
∵BD∥EF，
∴四边形AEDH和AHBF是矩形，
∴DE＝AH＝BF，
设DE＝AH＝BF＝h，
由题意知，∠BAF＝45°，∠CAF＝76°，∠DAE＝37°，BC＝30海里，
则∠BAH＝45°，∠ACH＝∠CAF＝76°，
∴∠ABH＝90°﹣∠BAH＝90°﹣45°＝45°，
∴∠ABH＝∠BAH，
∴BH＝AH＝h，
在Rt△ACH中，CH＝BH﹣BC＝h﹣30，tan∠ACH＝tan76°＝＝≈4，
∴h＝40，
∴AH＝40海里，
在Rt△ADH中，∠ADH＝∠DAH＝37°，
∴sin37°＝＝≈0.6，
∴AD≈67（海里），
答：相遇时快艇行驶的距离AD为67海里．

一十五．列表法与树状图法（共1小题）
18．（2023•鄄城县二模）（微信圈有篇热传的文章《如果想毁掉一个孩子，就给他一部手机！》，2021年教育部办公厅下发关于加强中小学生手机管理工作的通知，通知中提到：有限带入校园，细化管理措施，加强教育引导，做好家校沟通，强化督促检查五点学校管理措施，为了解学生手机使用情况，某学校组织开展了“手机伴我健康行”的主题活动，学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，图②的统计图，已知“查资料”的人数是40人．
​
（1）在这次调查中，一共抽取了 　100　名学生；
（2）在扇形统计图中，“玩游戏”对应的圆心角的度数是 　126　度；
（3）补全条形统计图；
（4）在使用手机“查资料”的学生中，恰有3人每周都是使用手机50分钟，其中2女1男，计划在这3个学生中随机抽选两个到全年级分享手机管理使用经验，请用列表或画树状图的方法求所选两个学生中有一个男生的概率．
【答案】（1）100．
（2）126．
（3）见解答．
（4）．
【解答】解：（1）在这次调查中，一共抽取的学生人数为40÷40%＝100（名）．
故答案为：100．
（2）在扇形统计图中，“玩游戏”对应的百分比为1﹣40%﹣18%﹣7%＝35%，
∴“玩游戏”对应的圆心角的度数是360°×35%＝126°．
故答案为：126．
（3）每周使用手机的时间在3小时以上的学生人数为100﹣2﹣16﹣18﹣32＝32（人）．
补全条形统计图如图②所示．

（4）设这3个学生中，2名女生分别记为A，B，1名男生记为C，
画树状图如下：

共有6种等可能的结果，其中所选两个学生中有一个男生的结果有：AC，BC，CA，CB，共4种，
∴所选两个学生中有一个男生的概率为＝．