山东省济宁市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（提升题）

这是一份山东省济宁市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（提升题），共41页。试卷主要包含了先化简，再求值，之间的函数图象，符合一次函数关系，之间成一次函数关系，，与y轴交于点C，且OB＝OC等内容，欢迎下载使用。
山东省济宁市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（提升题）
一．分式的化简求值（共1小题）
1．（2023•任城区二模）先化简，再求值：﹣÷，其中x＝2．
二．一元一次不等式组的应用（共1小题）
2．（2023•微山县二模）某小区积极响应全民健身运动，决定在小区内安装健身器材．经调查：甲种健身器材的单价是乙种健身器材的单价的2倍，购买2个甲种健身器材和3个乙种健身器材共需420元．
（1）求甲、乙种健身器材的单价各是多少元？
（2）如果购买甲、乙种健身器材共60个，且费用不超过4800元．又知该小区至少需要安放19个甲种健身器材，请你列举出所有购买方案，并指出哪种方案所需资金最少？
三．一次函数的应用（共1小题）
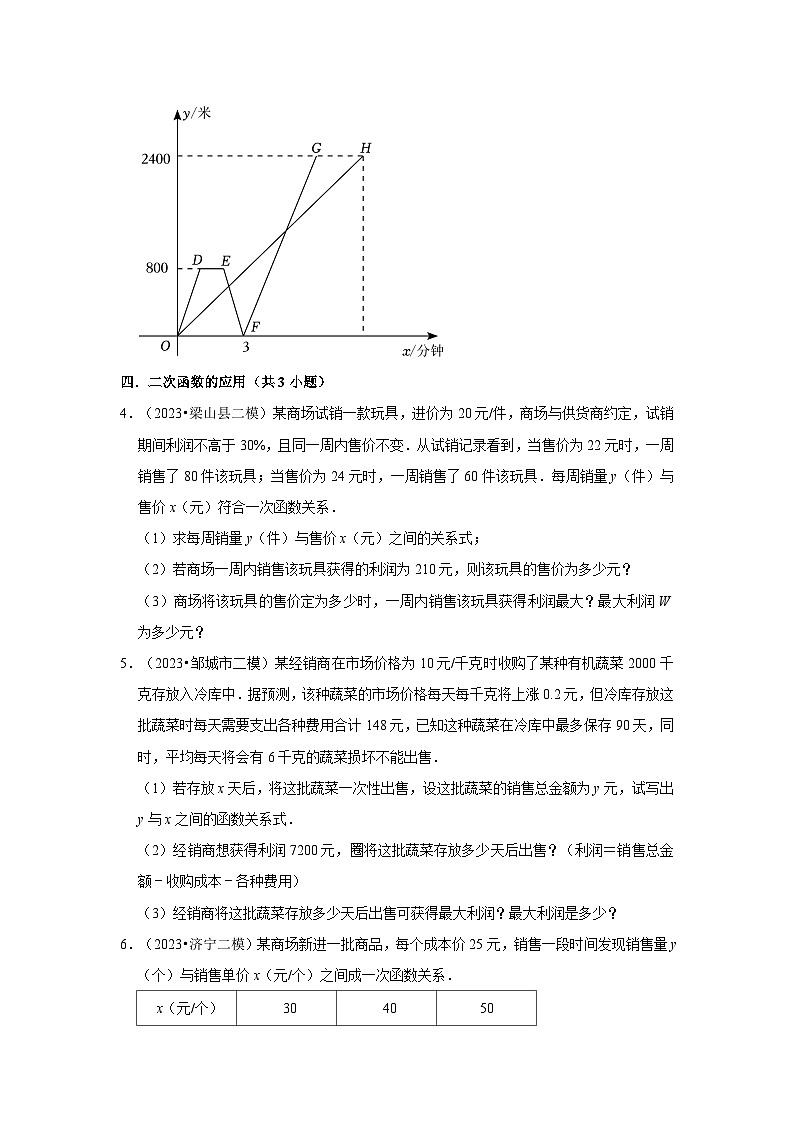
3．（2023•嘉祥县二模）在一条平坦笔直的道路上依次有A，B，C三地，甲从B地骑电瓶车到C地，同时乙从B地骑摩托车到A地，到达A地后因故停留1分钟，然后立即掉头（掉头时间忽略不计）按原路原速前往C地，结果乙比甲早2分钟到达C地，两人均匀速运动，如图是两人距B地路程y（米）与时间x（分钟）之间的函数图象．

请解答下列问题：
（1）填空：甲的速度为 　 　米/分钟，乙的速度为 　 　米/分钟；
（2）求图象中线段FG所在直线表示的y（米）与时间x（分钟）之间的函数解析式，并写出自变量x的取值范围．

四．二次函数的应用（共3小题）
4．（2023•梁山县二模）某商场试销一款玩具，进价为20元/件，商场与供货商约定，试销期间利润不高于30%，且同一周内售价不变．从试销记录看到，当售价为22元时，一周销售了80件该玩具；当售价为24元时，一周销售了60件该玩具．每周销量y（件）与售价x（元）符合一次函数关系．
（1）求每周销量y（件）与售价x（元）之间的关系式；
（2）若商场一周内销售该玩具获得的利润为210元，则该玩具的售价为多少元？
（3）商场将该玩具的售价定为多少时，一周内销售该玩具获得利润最大？最大利润W为多少元？
5．（2023•邹城市二模）某经销商在市场价格为10元/千克时收购了某种有机蔬菜2000千克存放入冷库中．据预测，该种蔬菜的市场价格每天每千克将上涨0.2元，但冷库存放这批蔬菜时每天需要支出各种费用合计148元，已知这种蔬菜在冷库中最多保存90天，同时，平均每天将会有6千克的蔬菜损坏不能出售．
（1）若存放x天后，将这批蔬菜一次性出售，设这批蔬菜的销售总金额为y元，试写出y与x之间的函数关系式．
（2）经销商想获得利润7200元，圈将这批蔬菜存放多少天后出售？（利润＝销售总金额﹣收购成本﹣各种费用）
（3）经销商将这批蔬菜存放多少天后出售可获得最大利润？最大利润是多少？
6．（2023•济宁二模）某商场新进一批商品，每个成本价25元，销售一段时间发现销售量y（个）与销售单价x（元/个）之间成一次函数关系．
x（元/个）
30
40
50
y（个）
190
170
150
（1）根据表中提供的数据，求y与x之间的函数关系式；
（2）若该商品的销售单价在45元～80元之间浮动．
①销售单价定为多少元时，销售利润最大？此时销售量为多少？
②商店想要在这段时间内获得4550元的销售利润，销售单价应定为多少元？
五．二次函数综合题（共3小题）
7．（2023•曲阜市二模）如图，已知直线与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+4经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．
（1）求抛物线的表达式；
（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；
（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．

8．（2023•任城区二模）如图，抛物线y＝ax2﹣2ax﹣3a（a＞0）与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，且OB＝OC．
（1）求抛物线的解析式；
（2）如图，若点P是线段BC（不与B，C重合）上一动点，过点P作x轴的垂线交抛物线于M点，连接CM，当△PCM和△ABC相似时，求此时点P的坐标；
（3）若点P是直线BC（不与B，C重合）上一动点，过点P作x轴的垂线交抛物线于M点，连接CM，将△PCM沿CM对折，如果点P的对应点N恰好落在y轴上，求此时点P的坐标；

9．（2023•济宁二模）已知：m、n是方程x2﹣6x+5＝0的两个实数根，且m＜n，抛物线y＝﹣x2+bx+c的图象经过点A（m，0）、B（0，n）．
（1）求这个抛物线的解析式；
（2）设（1）中抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；（注：抛物线y＝ax2+bx+c（a≠0）的顶点坐标为
（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标．

六．切线的判定（共1小题）
10．（2023•邹城市二模）如图，AB为⊙O的直径，CO⊥AB于点O，D在⊙O上，连接BD、CD，延长CD与AB的延长线交于E，F在BE上，且FD＝FE．
（1）求证：FD是⊙O的切线；
（2）若AF＝10，tan∠BDF＝，求EF的长．

七．切线的判定与性质（共2小题）
11．（2023•梁山县二模）如图，AB是⊙O的直径，C，D都是⊙O上的点，AD平分∠CAB，过点D作AC的垂线交AC的延长线于点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）若AB＝10，AC＝6，求CE的值．

12．（2023•微山县二模）如图，△ABC中，∠C＝90°，∠ABC的平分线交AC于点D，点O在AB上，以点O为圆心，以OB为半径的圆经过点D，交BC于点E，交AB于点F．

（1）求证：AC与⊙O相切；
（2）若BD＝10，，求AF的长．

八．圆的综合题（共1小题）
13．（2023•微山县二模）

探究问题
探究与的大小关系．
（1）观察猜想
与的大小关系是　 　．
（2）计算验证
当a＝8，b＝8时，与的大小关系是　 　；
当a＝2，b＝6时，与的大小关系是　 　．
（3）推理证明
如图，以AB为直径作半圆O，点C半圆上一动点，过C作CD⊥AB于点D，设AD＝a，BD＝b．先用含a，b的式子表示出线段OC，CD，再写出他们（含a，b的式子）之间存在的大小关系．
实践应用
要制作一个面积为1平方米的矩形，请直接利用探究得出的结论，求矩形周长的最小值．

九．相似三角形的判定与性质（共1小题）
14．（2023•兖州区二模）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D为的中点，⊙O的切线DE交OC的延长线于点E．
（1）求证：DE∥AC；
（2）连接BD交AC于点P，若AC＝8，cosA＝，求DE和BP的长．

一十．解直角三角形的应用（共1小题）
15．（2023•金乡县二模）太阳能光伏发电因其清洁、安全、高效等特点，已成为世界各国重点发展的新能源产业．图①是太阳能电板的实物图，其截面示意图如图②，AB为太阳能电板，其一端A固定在水平面上且夹角∠DAB＝22°，另一端B与支撑钢架BC相连，钢架底座CD和水平面垂直，且∠BCD＝135°．若AD＝3m，CD＝0.5m，求AB的长．（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，结果精确到0.01m．）

一十一．解直角三角形的应用-方向角问题（共1小题）
16．（2023•济宁二模）酒驾猛于虎，但很多人不以为是，为了加强人们对酒驾危害的认识，交警部门加大了对酒驾的检查力度．某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查，如图，AC是该市解放路的一段，AE，BF，CD都是南北方向的街道，与解放路AC的交叉路口分别是A，B，C．已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上，BD＝2km，∠DBC＝30°．
（1）求A、B的距离；
（2）第一组交警负责路口A，求该组从出警点D到路口A的路程（行驶路线为D﹣﹣C﹣﹣B﹣﹣A）．（结果保留根号）

一十二．频数（率）分布直方图（共1小题）
17．（2023•邹城市二模）初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题．

（1）在这次评价中，一共抽查了 　 　名学生；
（2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为 　 　度；
（3）请将频数分布直方图补充完整；
（4）如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？
一十三．列表法与树状图法（共3小题）
18．（2023•曲阜市二模）2022年3月23日下午，“天宫课堂”第二课在中国空间站开讲，神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课，这是中国空间站的第二次太空授课，被许多中小学生称为“最牛网课”．某中学为了解学生每周参与“航空航天知识”学习的累计时间t（单位：小时），学校采用随机抽样的方法，对部分学生进行了问卷调查，调查结果按0≤t＜3，3≤t＜4，4≤t＜5，t≥5分为四个等级，分别用A、B、C、D表示，如图是受损的调查统计图，请根据图上残存信息解决以下问题：

（1）求参与问卷调查的学生人数n，并将条形统计图补充完整；
（2）全校共有学生2000人，试估计学校每周参与“航空航天知识”学习累计时间不少于4小时的学生人数；
（3）某小组有4名同学，A、D等级各2人，从中任选2人向老师汇报学习情况，请用画树状图法或列表法求这2人均属D等级的概率．
19．（2023•微山县二模）某校九年级一班综合实践活动小组的同学以“知道乱扔垃圾的危害吗？”为主题，随机调查了某社区部分居民，并对调查结果进行了整理，绘制了如下不完整的统计表及统计图，观察并解答下列问题：
类别
乱扔垃圾的危害
百分比
A
非常了解
45%
B
了解
m
C
一般
15%
D
不了解
n
（1）求本次被调查居民的人数及m，n的值，并补全条形统计图；
（2）若该社区有1600人口，估计B，C两类居民共有多少人？
（3）小明同学在四个质地、大小、形状都完全相同的小球标记上A，B，C，D（代表乱扔垃圾的危害知道情况），并放在一个不透明的盒子中，他先随机抽取一个小球，放回去，再随机抽取一个小球，请用画树状图或列表的方法，求小明同学刚好抽到B和D的概率．

20．（2023•金乡县二模）为落实德州市关于开展中小学课后服务工作的要求，某学校开展了四门校本课程供学生选择：A．趣味数学；B．博乐阅读；C．快乐英语；D．硬笔书法．全校共有100名学生选择了A课程，为了解选A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试．将他们的成绩（百分制）绘制成频数分布直方图．
（1）其中70≤x＜80这一组的数据为74，73，72，75，76，76，79，则这组数据的中位数是 　 　，众数是 　 　．
（2）根据题中信息，估计该校共有 　 　人，选A课程学生成绩在80≤x＜90的有 　 　人．
（3）课程D在扇形统计图中所对应的圆心角的度数为 　 　．
（4）如果学校规定每名学生要选两门不同的课程，小张和小王在选课程中，若第一次都选了课程C，那么他俩第二次同时选课程A或B的概率是多少？请用列表法或画树状图的方法加以说明．


山东省济宁市2023年各地区中考考数学模拟（二模）试题按题型难易度分层分类汇编-03解答题（提升题）
参考答案与试题解析
一．分式的化简求值（共1小题）
1．（2023•任城区二模）先化简，再求值：﹣÷，其中x＝2．
【答案】见试题解答内容
【解答】解：原式＝﹣•（x+1）＝﹣＝，
当x＝2时，原式＝2．
二．一元一次不等式组的应用（共1小题）
2．（2023•微山县二模）某小区积极响应全民健身运动，决定在小区内安装健身器材．经调查：甲种健身器材的单价是乙种健身器材的单价的2倍，购买2个甲种健身器材和3个乙种健身器材共需420元．
（1）求甲、乙种健身器材的单价各是多少元？
（2）如果购买甲、乙种健身器材共60个，且费用不超过4800元．又知该小区至少需要安放19个甲种健身器材，请你列举出所有购买方案，并指出哪种方案所需资金最少？
【答案】（1）甲种健身器材的单价是120元，乙种健身器材的单价是60元；
（2）当购买甲健身器材19台，乙健身器材41台，所需资金最小．
【解答】解：（1）设乙种健身器材的单价是x元，则甲种健身器材的单价是2x元，
根据题意得2×2x+3x＝420，
解得x＝60，2x＝120，
答：甲种健身器材的单价是120元，乙种健身器材的单价是60元；
（2）设购买甲种健身器材y个，则购买乙种健身器材（60﹣y）个，
根据题意得，
解得19≤y≤20，
∵y为整数，
∴y可以为19，20，
∴一共有2种购买方案，
方案1：购买甲健身器材19台，乙健身器材41台；
需要资金，120×19+60×41＝4740（元）；
方案2：购买甲健身器材20台，乙健身器材40台；
需要资金，120×20+60×40＝4800（元）；
∵4740＜4800，
∴当购买甲健身器材19台，乙健身器材41台，所需资金最小，最小值为4740元．
三．一次函数的应用（共1小题）
3．（2023•嘉祥县二模）在一条平坦笔直的道路上依次有A，B，C三地，甲从B地骑电瓶车到C地，同时乙从B地骑摩托车到A地，到达A地后因故停留1分钟，然后立即掉头（掉头时间忽略不计）按原路原速前往C地，结果乙比甲早2分钟到达C地，两人均匀速运动，如图是两人距B地路程y（米）与时间x（分钟）之间的函数图象．

请解答下列问题：
（1）填空：甲的速度为 　300　米/分钟，乙的速度为 　800　米/分钟；
（2）求图象中线段FG所在直线表示的y（米）与时间x（分钟）之间的函数解析式，并写出自变量x的取值范围．

【答案】（1）300；800；
（2）y＝800x﹣2400（3≤x≤6）．
【解答】解：（1）根据题意可知D（1，800），E（2，800），
∴乙的速度为：800÷1＝800（米/分钟），
∴乙从B地到C地用时：2400÷800＝3（分钟），
∴G（6，2400）．
∴H（8，2400）．
∴甲的速度为2400÷8＝300（米/分钟），
故答案为：300；800；
（2）设直线FG的解析式为：y＝kx+b（k≠0），且由图象可知F（3，0），
由（1）知G（6，2400）．
∴，
解得，．
∴直线FG的解析式为：y＝800x﹣2400（3≤x≤6）．
四．二次函数的应用（共3小题）
4．（2023•梁山县二模）某商场试销一款玩具，进价为20元/件，商场与供货商约定，试销期间利润不高于30%，且同一周内售价不变．从试销记录看到，当售价为22元时，一周销售了80件该玩具；当售价为24元时，一周销售了60件该玩具．每周销量y（件）与售价x（元）符合一次函数关系．
（1）求每周销量y（件）与售价x（元）之间的关系式；
（2）若商场一周内销售该玩具获得的利润为210元，则该玩具的售价为多少元？
（3）商场将该玩具的售价定为多少时，一周内销售该玩具获得利润最大？最大利润W为多少元？
【答案】（1）y＝﹣10x+300；
（2）23元；
（3）25元，250元．
【解答】（1）解：（1）设每周销量y（件）与销售单价x（元）之间的关系式为y＝kx+b，
则，
解得：，
∴y（件）与销售单价x（元）之间的关系式为：y＝﹣10x+300．
故答案为：y＝﹣10x+300；
（2）解：根据题意可得（x﹣20）（﹣10x+300）＝210，
整理得：x2﹣50x+621＝0，
解得：x1＝23，x2＝27，
∵利润不高于30%，
∴x≤20×（1+30%）＝26，
∴x2＝27（舍去），
∴x＝23．
答：该玩具的售价为23元．
故答案为：23元．
（3）根据题意得：W＝（x﹣20）（﹣10x+300）＝﹣10x2+500x﹣6000＝﹣10（x﹣25）2+250，
∵a＝﹣10＜0，
∴W随着x的减小而增大，
∴当x＝25时，W取最大值且W＝250元．
答：最大利润W为250元．
故答案为：250元．
5．（2023•邹城市二模）某经销商在市场价格为10元/千克时收购了某种有机蔬菜2000千克存放入冷库中．据预测，该种蔬菜的市场价格每天每千克将上涨0.2元，但冷库存放这批蔬菜时每天需要支出各种费用合计148元，已知这种蔬菜在冷库中最多保存90天，同时，平均每天将会有6千克的蔬菜损坏不能出售．
（1）若存放x天后，将这批蔬菜一次性出售，设这批蔬菜的销售总金额为y元，试写出y与x之间的函数关系式．
（2）经销商想获得利润7200元，圈将这批蔬菜存放多少天后出售？（利润＝销售总金额﹣收购成本﹣各种费用）
（3）经销商将这批蔬菜存放多少天后出售可获得最大利润？最大利润是多少？
【答案】（1）y＝﹣1.2x2+340x+20000（1≤x≤90）；
（2）经销商想获得利润7200元需将这批蔬菜存放60天后出售；
（3）存放80天后出售这批蔬菜可获得最大利润7680元．
【解答】解：（1）由题意得y与x之间的函数关系式为：
y＝（10+0.2x）（2000﹣6x）＝﹣1.2x2+340x+20000（1≤x≤90）；

（2）由题意得：﹣1.2x2+340x+20000﹣10×2000﹣148x＝7200，
解方程得：x1＝60；x2＝100（不合题意，舍去），
经销商想获得利润7200元需将这批蔬菜存放60天后出售；

（3）设最大利润为W元，
由题意得W＝﹣1.2x2+340x+20000﹣10×2000﹣148x
即W＝﹣1.2（x﹣80）2+7680，
∴当x＝80时，W最大＝7680，
由于80＜90，
∴存放80天后出售这批蔬菜可获得最大利润7680元．
6．（2023•济宁二模）某商场新进一批商品，每个成本价25元，销售一段时间发现销售量y（个）与销售单价x（元/个）之间成一次函数关系．
x（元/个）
30
40
50
y（个）
190
170
150
（1）根据表中提供的数据，求y与x之间的函数关系式；
（2）若该商品的销售单价在45元～80元之间浮动．
①销售单价定为多少元时，销售利润最大？此时销售量为多少？
②商店想要在这段时间内获得4550元的销售利润，销售单价应定为多少元？
【答案】见试题解答内容
【解答】解：（1）设y＝kx+b（k≠0），由题意得，
，
解得：．
∴y＝﹣2x+250．
（2）①设该商品的利润为W，
∴W＝（﹣2x+250）×（x﹣25）＝﹣2x2+300x﹣6250＝﹣2（x﹣75）2+5000，
∵﹣2＜0，
∴当x＝75时，W最大，此时的销售量为：y＝﹣2×75+250＝100（个）．
②当获得4550元的销售利润时，
﹣2（x﹣75）2+5000＝4550，
解得：x1＝60，x2＝90，
∵该商品的销售单价在45元～80元之间浮动，
∴x＝60．
答：销售单价应定为60元．
五．二次函数综合题（共3小题）
7．（2023•曲阜市二模）如图，已知直线与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+4经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x＝﹣1．
（1）求抛物线的表达式；
（2）D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；
（3）若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．

【答案】（1）；（2）（﹣1.5，5）；（3）存在，，．
【解答】解：（1）对于，当x＝0时，y＝4，当y＝0时，x＝﹣3，
∴点A的坐标为（﹣3，0），点C的坐标为（0，4），
∵对称轴是直线：x＝﹣1，
∴有：，解得：，
∴抛物线的表达式为：；
（2）对于，当y＝0时，，解得：x1＝3，x2＝1，
∴点B的坐标为（0，1），
又∵点A（﹣3，0），点C（0，4），
∴OA＝3，OB＝1，OC＝4
作DE⊥x轴于E，

∵点D在第二象限内的抛物线上，且横坐标为m
∴点D的坐标为（m，n），则，
∴OE＝﹣m，DE＝n，
∴AE＝OA﹣OE＝3﹣（﹣m）＝m+3，
∵DE⊥x轴，则四边形OCDE为直角梯形，
∴，
又，，
∴S＝S四边形OCDE+S△ADE+S△BOC，
即，
又，
，
当m＝﹣1.5时，S为最大，
此时
∴点D的坐标为（﹣1.5，5）．
（3）存在点P和点Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形，理由如下：
∵点P在抛物线的对称轴x＝﹣1上，
∴可设点P的坐标为：（﹣1，t），
∵以A，C，P，Q为顶点的四边形是以AC为对角线的菱形，
∴PA＝PC＝QA＝QC，AC与PQ互相垂直平分，
设直线x＝﹣1与x轴交于点F，过点P作PT⊥y轴，AC与PQ交于点K，

∵点A（﹣3，0），C（0，4），
∴OA＝3，CO＝4，OF＝PT＝1，OT＝PF＝t，
∴AF＝OA﹣OF＝3﹣1＝2，CT＝OC﹣OT＝4﹣t，
在Rt△APF中，由勾股定理得：PA2＝PF2+AF2＝t2+4，
在Rt△CPT中，由勾股定理得：PC2＝PT2+CT2＝1+（4﹣t）2
∴t2+4＝1+（4﹣t）2，解得：，
∴点P的坐标为，
设点K的坐标为（xK，yK），
∵点K为AC的中点，
∴，，
设点Q的坐标为（xQ，yQ），
∵点K为PQ的中点，
∴，，
解得：xQ＝﹣2，，
∴点Q的坐标为．
8．（2023•任城区二模）如图，抛物线y＝ax2﹣2ax﹣3a（a＞0）与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，且OB＝OC．
（1）求抛物线的解析式；
（2）如图，若点P是线段BC（不与B，C重合）上一动点，过点P作x轴的垂线交抛物线于M点，连接CM，当△PCM和△ABC相似时，求此时点P的坐标；
（3）若点P是直线BC（不与B，C重合）上一动点，过点P作x轴的垂线交抛物线于M点，连接CM，将△PCM沿CM对折，如果点P的对应点N恰好落在y轴上，求此时点P的坐标；

【答案】（1）y＝x2﹣2x﹣3；
（2）（，﹣）或（，﹣）；
（3）（3﹣，﹣）或（3+，）．
【解答】解：（1）在y＝ax2﹣2ax﹣3a（a＞0）中，
令y＝0，得：ax2﹣2ax﹣3a＝0，
解得：x1＝3，x2＝﹣1，
∴A（﹣1，0），B（3，0），
∴OB＝3，
∵OB＝OC，
∴OC＝3，
∴C（0，﹣3），
∴﹣3a＝﹣3，
∴a＝1，
∴抛物线解析式为：y＝x2﹣2x﹣3；
（2）设直线BC解析式为y＝kx+b，
∵B（3，0），C（0，﹣3），
∴，解得：，
∴直线BC解析式为：y＝x﹣3，
设M点坐标为（m，m2﹣2m﹣3），
∵PM⊥x轴，
∴P（m，m﹣3），
∴PM＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，
∵OB＝OC，∠BOC＝90°，
∴CB＝OB，
∴CP＝m，
∵A（﹣1，0），B（3，0），C（0，﹣3），
∴OB＝OC，AC＝，BC＝3，
∴∠PBA＝∠OCB＝45°＝∠MPC，
若△PCM和△ABC相似，分两种情况：
①当△CPM∽△CBA，
∴，即，
解得：m＝，
∴P（，﹣）；
②当△CPM∽△ABC，
∴，即，
解得：m＝，
∴P（，﹣）；
综上所述，点P的坐标为（，﹣）或（，﹣）；
（3）设M点坐标为（m，m2﹣2m﹣3），
当点P在M的上方时，由（2）知PM＝﹣m2+3m，CP＝m，

∵△PCM沿CM对折，点P的对应点N恰好落在y轴上，
∴∠PCM＝∠NCM，
∵PM∥y轴，
∴∠NCM＝∠PMC，
∴∠PCM＝∠PMC，
∴PC＝PM，
∴m＝﹣m2+3m，
整理得：m2+（﹣3）m＝0，
解得：m1＝0（舍去），m2＝3﹣，
∴当m＝3﹣时，m﹣3＝﹣，
∴P（3﹣，﹣）．
当点P在M点下方时，PM＝m2﹣3m，
同理可得m＝m2﹣3m，
解得m1＝0（舍去），m2＝3+，
∴P（3+，），
综上所述，点P的坐标为（3﹣，﹣）或（3+，）．
9．（2023•济宁二模）已知：m、n是方程x2﹣6x+5＝0的两个实数根，且m＜n，抛物线y＝﹣x2+bx+c的图象经过点A（m，0）、B（0，n）．
（1）求这个抛物线的解析式；
（2）设（1）中抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；（注：抛物线y＝ax2+bx+c（a≠0）的顶点坐标为
（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标．

【答案】见试题解答内容
【解答】解：（1）解方程x2﹣6x+5＝0，
（x﹣1）（x﹣5）＝0，
得x1＝5，x2＝1
由m＜n，有m＝1，n＝5
所以点A、B的坐标分别为A（1，0），B（0，5）．
将A（1，0），B（0，5）的坐标分别代入y＝﹣x2+bx+c．
得，
解这个方程组，得：

所以，抛物线的解析式为y＝﹣x2﹣4x+5

（2）由y＝﹣x2﹣4x+5，令y＝0，得﹣x2﹣4x+5＝0，
解这个方程，得x1＝﹣5，x2＝1，
所以C点的坐标为（﹣5，0）．由顶点坐标公式计算，得点D（﹣2，9）．
过D作x轴的垂线交x轴于M．
则S△DMC＝×9×（5﹣2）＝
S梯形MDBO＝×2×（9+5）＝14，
S△BOC＝×5×5＝，
所以，S△BCD＝S梯形MDBO+S△DMC﹣S△BOC＝14+﹣＝15．

（3）设P点的坐标为（a，0）
因为线段BC过B、C两点，
所以BC所在的直线方程为y＝x+5．
那么，PH与直线BC的交点坐标为E（a，a+5），
PH与抛物线y＝﹣x2﹣4x+5的交点坐标为H（a，﹣a2﹣4a+5）．
由题意，得①EH＝EP，
即（﹣a2﹣4a+5）﹣（a+5）＝（a+5）
解这个方程，得a＝﹣或a＝﹣5（舍去）
②EH＝EP，即（﹣a2﹣4a+5）﹣（a+5）＝（a+5）
解这个方程，得a＝﹣或a＝﹣5（舍去），
P点的坐标为（﹣，0）或（﹣，0）．


六．切线的判定（共1小题）
10．（2023•邹城市二模）如图，AB为⊙O的直径，CO⊥AB于点O，D在⊙O上，连接BD、CD，延长CD与AB的延长线交于E，F在BE上，且FD＝FE．
（1）求证：FD是⊙O的切线；
（2）若AF＝10，tan∠BDF＝，求EF的长．

【答案】见试题解答内容
【解答】（1）证明：连接OD，如图，
∵CO⊥AB，
∴∠E+∠C＝90°，
∵FE＝FD，OD＝OC，
∴∠E＝∠FDE，∠C＝∠ODC，
∴∠FDE+∠ODC＝90°，
∴∠ODF＝90°，
∴OD⊥DF，
∴FD是⊙O的切线；
（2）解：连接AD，如图，
∵AB为⊙O的直径，
∴∠ADB＝90°，
∴∠A+∠ABD＝90°，
∵OB＝OD，
∴∠OBD＝∠ODB，
∴∠A+∠ODB＝90°，
∵∠BDF+∠ODB＝90°，
∴∠A＝∠BDF，
而∠DFB＝∠AFD，
∴△FBD∽△FDA，
∴＝，
在Rt△ABD中，tan∠A＝tan∠BDF＝＝，
∴＝，
∴DF＝2.5，
∴EF＝2.5．

七．切线的判定与性质（共2小题）
11．（2023•梁山县二模）如图，AB是⊙O的直径，C，D都是⊙O上的点，AD平分∠CAB，过点D作AC的垂线交AC的延长线于点E，交AB的延长线于点F．
（1）求证：EF是⊙O的切线；
（2）若AB＝10，AC＝6，求CE的值．

【答案】（1）见解答；
（2）2．
【解答】（1）证明：如图1，连接OD，

∵AD平分∠CAB，
∴∠OAD＝∠EAD，
∵OD＝OA，
∴∠ODA＝∠OAD，
∴∠ODA＝∠EAD，
∴OD∥AE，
∵∠ODF＝∠AEF＝90°且D在⊙O上，
∴EF是⊙O的切线；
（2）连接BC，交OD于H，

∵AB是⊙O的直径，
∴∠ACB＝90°，
∵AB＝10，AC＝6，
∴BC＝＝＝8，
∵∠E＝∠ACB＝90°，
∴BC∥EF，
∴∠OHB＝∠ODF＝90°，
∴OD⊥BC，
∴CH＝BC＝4，
∵CH＝BH，OA＝OB，
∴OH＝AC＝3，
∴DH＝5﹣3＝2，
∵∠E＝∠HCE＝∠EDH＝90°，
∴四边形ECHD是矩形，
∴ED＝CH＝4，CE＝DH＝2．
12．（2023•微山县二模）如图，△ABC中，∠C＝90°，∠ABC的平分线交AC于点D，点O在AB上，以点O为圆心，以OB为半径的圆经过点D，交BC于点E，交AB于点F．

（1）求证：AC与⊙O相切；
（2）若BD＝10，，求AF的长．

【答案】（1）见解析；
（2）．
【解答】（1）证明：连接OD，
∵OD是半径
∴OD＝OB，

∴∠ODB＝∠OBD，
∵∠ABC的平分线交AC于点D，
∴∠ABD＝∠CBD，
∴∠ODB＝∠CBD，
∴OD∥BC，
∴∠ADO＝∠C＝90°，
∴AC是⊙O的切线；
（2）解：连接DF，
∵＝＝，
∴CD＝6，
∴BC＝8，
∵FB为直径，
∴∠BDF＝90°，
∴∠BDF＝∠C，
∵∠CBD＝∠FBD，
∴△CDB∽△DFB，
∴，
∴BF＝，
∴OD＝OE＝OB＝，
∵OD∥BC，
∴△ADO∽△ACB，
∴，即：＝，
解得：AF＝．
八．圆的综合题（共1小题）
13．（2023•微山县二模）

探究问题
探究与的大小关系．
（1）观察猜想
与的大小关系是　≥　．
（2）计算验证
当a＝8，b＝8时，与的大小关系是　＝　；
当a＝2，b＝6时，与的大小关系是　＞　．
（3）推理证明
如图，以AB为直径作半圆O，点C半圆上一动点，过C作CD⊥AB于点D，设AD＝a，BD＝b．先用含a，b的式子表示出线段OC，CD，再写出他们（含a，b的式子）之间存在的大小关系．
实践应用
要制作一个面积为1平方米的矩形，请直接利用探究得出的结论，求矩形周长的最小值．

【答案】（1）≥；（2）＝；＞；（3）OC＝，CD＝，；矩形周长的最小值为4m．
【解答】解：（1）∵≥0，
∴a﹣2+b≥0，
∴a+b≥2，
∴．
故答案为：≥；
（2）∵当a＝8，b＝8时，＝＝8，＝＝8，
∴．
∵当a＝2，b＝6时，＝＝4，＝，
又∵4＞2，
∴．
故答案为：＝；＞；
（3）∵AD＝a，BD＝b，
∴AB＝AD+BD＝a+b，
∵AB为直径，
∴OC＝AB＝．
∵AB为直径，
∴∠ACB＝90°．
∵CD⊥AB，
∴△ACD∽△CBD，
∴，
∴CD2＝AD•BD＝ab，
∴CD＝．
∵OC≥CD（D，O重合时取等号），
∴．
要制作一个面积为1平方米的矩形，设矩形的一边长为xm，则另一边为 m，
∴矩形的周长为矩形周长的最小值2（x+）m，
由（2）知：x+≥2，
∴x+≥2，当x＝时取等号，即当x＝1时，
∴当x＝1时，该矩形的周长取得最小值，
∴矩形周长的最小值2（x+）＝4m．
答：要制作一个面积为1平方米的矩形，矩形周长的最小值为4．
九．相似三角形的判定与性质（共1小题）
14．（2023•兖州区二模）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，点D为的中点，⊙O的切线DE交OC的延长线于点E．
（1）求证：DE∥AC；
（2）连接BD交AC于点P，若AC＝8，cosA＝，求DE和BP的长．

【答案】（1）见解析；
（2）DE＝，BP＝3．
【解答】（1）证明：连接OD，

∵DE与⊙O相切于点D，
∴OD⊥DE，
∵点D为的中点，
∴OD⊥AC，
∴DE∥AC；
（2）解：连接OD与AC交于点H，连接AD，

∵AB是直径，
∴∠ACB＝90°，
∴AB＝，
∴BC＝，
∵点D为的中点，
∴AH＝CH＝4，OD∥BC，
∴OH＝，
∵OD＝AB＝5，
∴DH＝OD﹣OH＝5﹣3＝2，
∴AD＝，
∵AB为直径，
∴∠ADB＝90°，
∴BD＝，
∵OD∥BC，
∴△HPD∽△CBP，
∴，即，
∴BP＝3，
∵HC∥DE，
∴△OHC∽△ODE，
∴，即，
∴DE＝．
一十．解直角三角形的应用（共1小题）
15．（2023•金乡县二模）太阳能光伏发电因其清洁、安全、高效等特点，已成为世界各国重点发展的新能源产业．图①是太阳能电板的实物图，其截面示意图如图②，AB为太阳能电板，其一端A固定在水平面上且夹角∠DAB＝22°，另一端B与支撑钢架BC相连，钢架底座CD和水平面垂直，且∠BCD＝135°．若AD＝3m，CD＝0.5m，求AB的长．（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，结果精确到0.01m．）

【答案】AB的长约为2.70m．
【解答】解：∵∠BCD＝135°，∠FCD＝90°，
∴∠BCF＝45°，
∵∠BFC＝90°，
∴∠FBC＝∠FCB＝45°，
∴FB＝FC，
设FB＝FC＝xm，则DE＝xm，
∵AD＝3m，CD＝0.5m，
∴AE＝（3﹣x）m，BE＝（x+0.5）m，
∵tan∠BAE＝，∠BAE＝22°，tan22°＝0.40，
∴0.40＝，
解得x＝0.5，
∴BE＝1m，
∵sin∠BAE＝，
∴sin22°＝，
解得AB≈2.70m，
即AB的长约为2.70m．

一十一．解直角三角形的应用-方向角问题（共1小题）
16．（2023•济宁二模）酒驾猛于虎，但很多人不以为是，为了加强人们对酒驾危害的认识，交警部门加大了对酒驾的检查力度．某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查，如图，AC是该市解放路的一段，AE，BF，CD都是南北方向的街道，与解放路AC的交叉路口分别是A，B，C．已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上，BD＝2km，∠DBC＝30°．
（1）求A、B的距离；
（2）第一组交警负责路口A，求该组从出警点D到路口A的路程（行驶路线为D﹣﹣C﹣﹣B﹣﹣A）．（结果保留根号）

【答案】见试题解答内容
【解答】解：（1）如图，由题意得，∠EAD＝45°，∠FBD＝30°，∠DBC＝30°，
∴∠FBC＝∠FBD+∠DBC＝30°+30°＝60°．
∵AE∥BF∥CD，
∴∠FBC＝∠EAC＝60°，
∴∠DAB＝15°，
又∵∠DBC＝∠DAB+∠ADB，∠DBC＝30°，
∴∠ADB＝15°，
∴∠DAB＝∠ADB，
∴AB＝BD＝2km．
即A，B之间的距离为2km；

（2）过B作BO⊥DC，交直线DC于点O，
∵BF∥CD，
∴∠FBD＝∠BDC＝30°，
在Rt△DBO中，∵∠BOD＝90°，BD＝2，
∴DO＝2×cos30°＝2×＝，BO＝2×sin30°＝1．
在Rt△CBO中，∵∠BOC＝90°，∠CBO＝30°，
∴CO＝BOtan30°＝，
∴CD＝DO﹣CO＝﹣＝（km）．
∵∠BDC＝∠DBC＝30°，
∴CD＝BC＝，
∴该组从出警点D到路口A的路程即D﹣C﹣B﹣A的行驶距离为（+2）km．


一十二．频数（率）分布直方图（共1小题）
17．（2023•邹城市二模）初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题．

（1）在这次评价中，一共抽查了 　560　名学生；
（2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为 　54　度；
（3）请将频数分布直方图补充完整；
（4）如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？
【答案】（1）560；
（2）54；
（3）图形见解析过程；
（4）1800人．
【解答】解：（1）在这次评价中，一共抽查了224÷40%＝560名学生，
故答案为：560；
（2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为，
故答案为：54；
（3）讲解题目的学生有：560﹣（84+168+224）＝84（人），
补充完整的频数分布直方图如图所示；

（4）（人），
在试卷评讲课中，“独立思考”的初三学生约有1800人．
一十三．列表法与树状图法（共3小题）
18．（2023•曲阜市二模）2022年3月23日下午，“天宫课堂”第二课在中国空间站开讲，神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课，这是中国空间站的第二次太空授课，被许多中小学生称为“最牛网课”．某中学为了解学生每周参与“航空航天知识”学习的累计时间t（单位：小时），学校采用随机抽样的方法，对部分学生进行了问卷调查，调查结果按0≤t＜3，3≤t＜4，4≤t＜5，t≥5分为四个等级，分别用A、B、C、D表示，如图是受损的调查统计图，请根据图上残存信息解决以下问题：

（1）求参与问卷调查的学生人数n，并将条形统计图补充完整；
（2）全校共有学生2000人，试估计学校每周参与“航空航天知识”学习累计时间不少于4小时的学生人数；
（3）某小组有4名同学，A、D等级各2人，从中任选2人向老师汇报学习情况，请用画树状图法或列表法求这2人均属D等级的概率．
【答案】（1）100，补全图形见解答；
（2）900人；
（3）．
【解答】解：（1）参与问卷调查的学生人数n＝40÷40%＝100（人），
D等级人数为100﹣（40+15+10）＝35（人），
补全图形如下：

（2）2000×＝900（人），
答：估计学校每周参与“航空航天知识”学习累计时间不少于4小时的学生有900人；
（3）随机选出2人向老师汇报学习情况的表格如下：

A
A
D
D
A

（A，A）
（D，A）
（D，A）
A
（A，A）

（D，A）
（D，A）
D
（A，D）
（A，D）

（D，D）
D
（A，D
（A，D）
（D，D）

∴共有12种等可能结果，而选出2人中2人均属D等级有2种，
∴所求概率为＝．
19．（2023•微山县二模）某校九年级一班综合实践活动小组的同学以“知道乱扔垃圾的危害吗？”为主题，随机调查了某社区部分居民，并对调查结果进行了整理，绘制了如下不完整的统计表及统计图，观察并解答下列问题：
类别
乱扔垃圾的危害
百分比
A
非常了解
45%
B
了解
m
C
一般
15%
D
不了解
n
（1）求本次被调查居民的人数及m，n的值，并补全条形统计图；
（2）若该社区有1600人口，估计B，C两类居民共有多少人？
（3）小明同学在四个质地、大小、形状都完全相同的小球标记上A，B，C，D（代表乱扔垃圾的危害知道情况），并放在一个不透明的盒子中，他先随机抽取一个小球，放回去，再随机抽取一个小球，请用画树状图或列表的方法，求小明同学刚好抽到B和D的概率．

【答案】（1）m＝30%，n＝10%；补全条形统计图见解析；
（2）估计B，C两类居民共有720人；
（3）小明同学刚好抽到B和D的概率为．
【解答】解：（1）本次被调查居民的总人数为：90÷45%＝200（人）；
m＝60÷200＝30%，
n＝20÷200＝10%；
C类人数为：200×15%＝30（人），
补全条形统计图为：

（2）1600×（30%+15%）＝720（人），
所以估计B，C两类居民共有720人；
（3）画树状图为：

共有16种等可能的结果数，其中小明同学刚好抽到B和D的结果数为2，
所以小明同学刚好抽到B和D的概率＝．
20．（2023•金乡县二模）为落实德州市关于开展中小学课后服务工作的要求，某学校开展了四门校本课程供学生选择：A．趣味数学；B．博乐阅读；C．快乐英语；D．硬笔书法．全校共有100名学生选择了A课程，为了解选A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试．将他们的成绩（百分制）绘制成频数分布直方图．
（1）其中70≤x＜80这一组的数据为74，73，72，75，76，76，79，则这组数据的中位数是 　75　，众数是 　76　．
（2）根据题中信息，估计该校共有 　500　人，选A课程学生成绩在80≤x＜90的有 　30　人．
（3）课程D在扇形统计图中所对应的圆心角的度数为 　108°　．
（4）如果学校规定每名学生要选两门不同的课程，小张和小王在选课程中，若第一次都选了课程C，那么他俩第二次同时选课程A或B的概率是多少？请用列表法或画树状图的方法加以说明．

【答案】（1）75 76；
（2）500，30；
（3）108°；
（4）．
【解答】解：（1）把70≤x＜80这组的数据排序为：72，73，74，75，76，76，79，
则这组数据的中位数是75，众数是76，
故答案为：75 76；
（2）估计该校共有：100÷20%＝500（人），
选A课程学生成绩在80≤x＜90的有：100×＝30（人），
故答案为：500，30；
（3）课程D在扇形统计图中所对应的圆心角的度数为：360°×（1﹣20%﹣35%﹣15%）＝108°，
故答案为：108°；
（4）画树状图如下：

共有9种等可能的结果，小张和小王他俩第二次同时选课程A或B的结果有2种，
∴小张和小王他俩第二次同时选课程A或B的概率为．