山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-02填空题

这是一份山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-02填空题，共26页。试卷主要包含了因式分解等内容，欢迎下载使用。
山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-02填空题
一．规律型：数字的变化类（共1小题）
1．（2023•嘉祥县一模）a是不为2的有理数，我们把称为a的“哈利数”．如：3的哈利数”是＝﹣2，﹣2的“哈利数”是＝，已知a1＝3，a2是a1的“哈利数”，a3是a2的“哈利数”，a4是a3的“哈利数”，…，依此类推，则a2023＝　 　．
二．提公因式法与公式法的综合运用（共1小题）
2．（2023•济宁一模）因式分解：4a2b﹣b＝　 　．
三．根与系数的关系（共1小题）
3．（2023•济宁一模）若一元二次方程x2﹣3x﹣2＝0的两个实数根为a，b，则a﹣ab+b的值为 　 　．
四．由实际问题抽象出分式方程（共1小题）
4．（2023•梁山县一模）某商店以定进价一次性购进一种商品，3月份按一定售价销售，销售额为2400元，为扩大销售，减少库存，4月份在3月份售价基础上打9折销售，结果销售量增加30件，销售额增加840元．设该商店3月份这种商品的售价是x元，则根据题意所列方程为　 　．
五．解一元一次不等式（共1小题）
5．（2023•嘉祥县一模）关于x，y的方程组的解中x与y的和不小于5，则k的取值范围为 　 　．
六．函数自变量的取值范围（共1小题）
6．（2023•邹城市一模）函数y＝中自变量x的取值范围是 　 　．
七．一次函数与二元一次方程（组）（共1小题）
7．（2023•泗水县一模）已知关于x，y的方程组的解是，则直线y＝﹣x+b与y＝﹣3x+2的交点坐标为 　 　．
八．反比例函数系数k的几何意义（共1小题）
8．（2023•微山县一模）如图，A是双曲线上的一点，点C是AO的中点，过点C作y轴的垂线，垂足为D，交双曲线于点B，则△ABD的面积是 　 　．

九．反比例函数图象上点的坐标特征（共1小题）
9．（2023•金乡县一模）已知点A（1，y1），B（3，y2）在反比例函数y＝的图象上，且y1＜y2，则m的取值范围是 　 　．
一十．抛物线与x轴的交点（共1小题）
10．（2023•金乡县一模）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（1，0）、点B与y轴相交于点C（0，3），下列结论：①b＝﹣2；②B点坐标为（﹣3，0）；③抛物线的顶点坐标为（﹣1，3）；④直线y＝h与抛物线交于点D、E，若DE＜2，则h的取值范围是3＜h＜4；⑤在抛物线的对称轴上存在一点Q，使△QAC的周长最小，则Q点坐标为（﹣1，2）．其中正确的有 　 　．

一十一．平行线的性质（共1小题）
11．（2023•邹城市一模）如图，一条公路修到湖边时，需拐弯绕道而过，如果第一次拐的∠A＝120°，第二次拐的∠B＝150°，第三次拐的∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C＝　 　．

一十二．矩形的性质（共1小题）
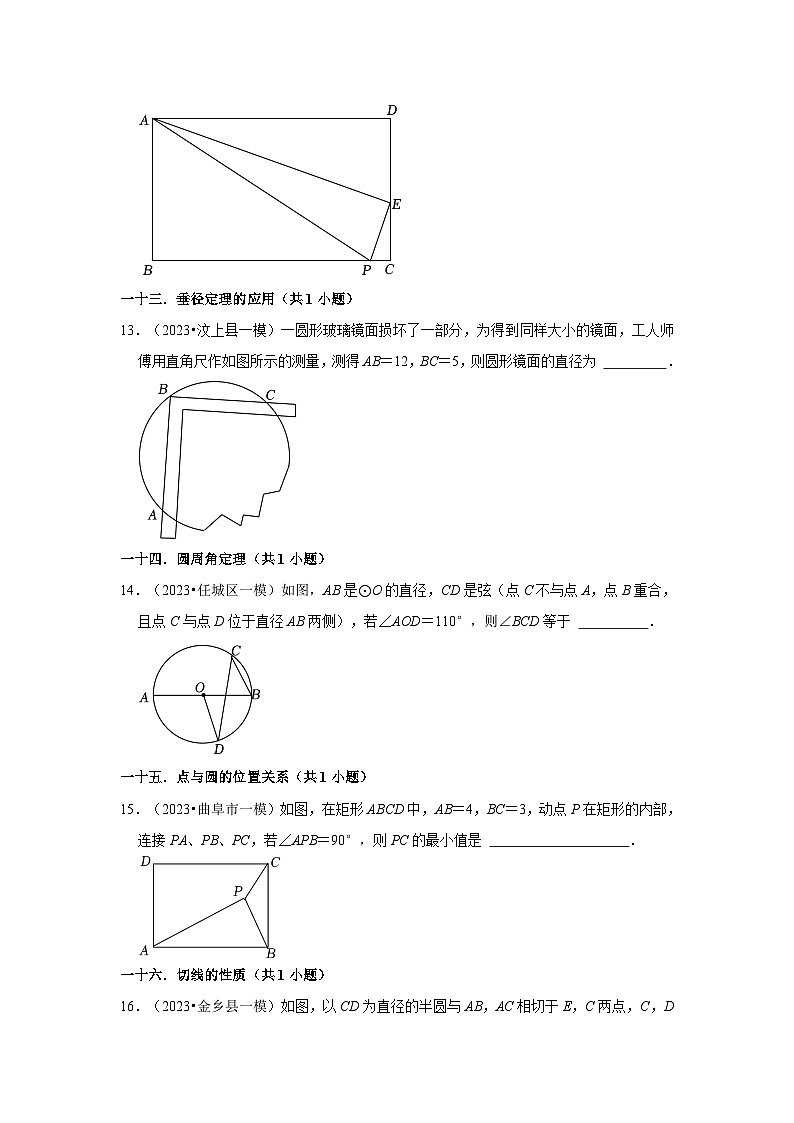
12．（2023•汶上县一模）如图，在矩形ABCD中，AB＝9，AD＝12，点E在边CD上，且CE＝4，点P是直线BC上的一个动点．若△APE是直角三角形，则CP的长为 　 　．

一十三．垂径定理的应用（共1小题）
13．（2023•汶上县一模）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12，BC＝5，则圆形镜面的直径为 　 　．

一十四．圆周角定理（共1小题）
14．（2023•任城区一模）如图，AB是⊙O的直径，CD是弦（点C不与点A，点B重合，且点C与点D位于直径AB两侧），若∠AOD＝110°，则∠BCD等于 　 　．

一十五．点与圆的位置关系（共1小题）
15．（2023•曲阜市一模）如图，在矩形ABCD中，AB＝4，BC＝3，动点P在矩形的内部，连接PA、PB、PC，若∠APB＝90°，则PC的最小值是 　 　．

一十六．切线的性质（共1小题）
16．（2023•金乡县一模）如图，以CD为直径的半圆与AB，AC相切于E，C两点，C，D，B三点共线，若弧DE的长为，CD＝2，则阴影部分的面积为 　 　．

一十七．扇形面积的计算（共2小题）
17．（2023•邹城市一模）如图，在△ABC，∠C＝90°，AC＝BC，斜边AB＝2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形ODE，点C在弧DE上，则图中阴影部分的面积为 　 　．

18．（2023•曲阜市一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AC＝6，以点A为圆心，AC为半径画弧交AB于点D，以点B为圆心，BC为半径画弧交AB于点E，则图中阴影部分的面积是 　 　（结果保留π）．

一十八．圆锥的计算（共1小题）
19．（2023•微山县一模）如图所示，矩形纸片ABCD中，AD＝3，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作一个圆锥的侧面和底面，则AB的长为 　 　．

一十九．作图—基本作图（共1小题）
20．（2023•泗水县一模）如图，在△ABC中，∠A＝30°，∠ABC＝100°，观察尺规作图的痕迹，则∠BFC的度数为 　 　．

二十．轴对称-最短路线问题（共1小题）
21．（2023•济宁一模）如图，在菱形ABCD中，AB＝4，∠ABC＝60°，点P是BD上一点，点M、N分别是BC、CD上任意一点，且PM⊥BC，垂足为M，连接PM、PN，则PM+PN的最小值为 　 　．

二十一．相似三角形的应用（共1小题）
22．（2023•任城区一模）将一张以AB为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形（剪掉的两个直角三角形相似），剩下的是如图所示的四边形纸片ABCD，其中∠A＝90°，AB＝9，BC＝7，CD＝6，AD＝2，则剪掉的两个直角三角形的斜边长可能是①；②；③10；④，其中正确的序号是 　 　．

二十二．解直角三角形的应用（共1小题）
23．（2023•微山县一模）为出行方便，近日来越来越多的市民使用起了共享单车，图1为单车实物图，图2为单车示意图，AB与地面平行，点A，B，D在同一条直线上，点D，F，G在同一条直线上，坐垫C可沿射线BE方向调节．已知，∠ABE＝70°，∠EAB＝45°，车轮半径为30cm，BE＝40cm．小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适，此时CE的长约为 　 　．（结果精确到1cm，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈1.41）

二十三．解直角三角形的应用-方向角问题（共1小题）
24．（2023•梁山县一模）一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西65°方向向海岛C靠近．同时，从A处出发的救援船沿南偏西10°方向匀速航行．20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为　 　．

二十四．众数（共1小题）
25．（2023•汶上县一模）为落实“双减”政策，济宁市某初中学校对学生的课外作业的时长进行了问卷调查．其中将抽查到的15名同学的作业时长统计如表，则这组数据的众数是 　 　．
作业时长（单位：分钟
50
60
70
80
90
人数（单位：人）
1
4
6
2
2
二十五．概率公式（共1小题）
26．（2023•微山县一模）一个不透明的盒子中装有3个黑球和2个白球，它们除颜色不同外，其余均相同，从盒子中随机摸出一个球是黑球的概率为 　 　．
二十六．列表法与树状图法（共1小题）
27．（2023•邹城市一模）“红灯停，绿灯行”是我们在日常生活中必须遵守的交通规则，这样才能保障交通顺畅和行人安全．小刚每天从家骑自行车上学都经过三个路口，且每个路口只安装了红灯和绿灯，假如每个路口红灯和绿灯亮的时间相同，那么小刚从家随时出发去学校，他遇到两次红灯的概率是 　 　．

山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-02填空题
参考答案与试题解析
一．规律型：数字的变化类（共1小题）
1．（2023•嘉祥县一模）a是不为2的有理数，我们把称为a的“哈利数”．如：3的哈利数”是＝﹣2，﹣2的“哈利数”是＝，已知a1＝3，a2是a1的“哈利数”，a3是a2的“哈利数”，a4是a3的“哈利数”，…，依此类推，则a2023＝　　．
【答案】．
【解答】解：∵a1＝3，
∴a2＝，
a3＝，
a4＝，
a5＝，
∴该数列每4个数为1周期循环，
∵2023÷4＝505……3，
∴a2023＝a3＝．
故答案为：．
二．提公因式法与公式法的综合运用（共1小题）
2．（2023•济宁一模）因式分解：4a2b﹣b＝　b（2a+1）（2a﹣1）　．
【答案】见试题解答内容
【解答】解：4a2b﹣b
＝b（4a2﹣1）
＝b（2a+1）（2a﹣1），
故答案为：b（2a+1）（2a﹣1）．
三．根与系数的关系（共1小题）
3．（2023•济宁一模）若一元二次方程x2﹣3x﹣2＝0的两个实数根为a，b，则a﹣ab+b的值为 　5　．
【答案】5．
【解答】解：∵一元二次方程x2﹣3x﹣2＝0的两个实数根为a，b，
∴a+b＝3，ab＝﹣2，
则原式＝（a+b）﹣ab＝3﹣（﹣2）＝3+2＝5．
故答案为：5．
四．由实际问题抽象出分式方程（共1小题）
4．（2023•梁山县一模）某商店以定进价一次性购进一种商品，3月份按一定售价销售，销售额为2400元，为扩大销售，减少库存，4月份在3月份售价基础上打9折销售，结果销售量增加30件，销售额增加840元．设该商店3月份这种商品的售价是x元，则根据题意所列方程为　＝﹣30　．
【答案】见试题解答内容
【解答】解：设该商店3月份这种商品的售价是x元，由题意得：
＝﹣30，
故答案为：＝﹣30．
五．解一元一次不等式（共1小题）
5．（2023•嘉祥县一模）关于x，y的方程组的解中x与y的和不小于5，则k的取值范围为 　k≥8　．
【答案】k≥8．
【解答】解：，
①﹣②，得x+y＝k﹣3，
根据题意得：k﹣3≥5，
解得k≥8．
所以k的取值范围是k≥8．
故答案为：k≥8．
六．函数自变量的取值范围（共1小题）
6．（2023•邹城市一模）函数y＝中自变量x的取值范围是 　x＞3　．
【答案】x＞3．
【解答】解：由题意得：
x﹣3＞0，
解得：x＞3，
故答案为：x＞3．
七．一次函数与二元一次方程（组）（共1小题）
7．（2023•泗水县一模）已知关于x，y的方程组的解是，则直线y＝﹣x+b与y＝﹣3x+2的交点坐标为 　（2，﹣4）　．
【答案】（﹣1，﹣1）．
【解答】解：把代入得：m＝3×（﹣1）+2＝﹣1，
∴关于x，y的方程组的解是，
即：﹣1＝﹣（﹣1）+b，解得：b＝﹣2，
则有直线y＝﹣x+b为：y＝﹣x﹣2；
联立，解得：，
∴直线y＝﹣x+b与y＝﹣3x+2的交点坐标为（﹣1，﹣1），
故答案为：（﹣1，﹣1）．
八．反比例函数系数k的几何意义（共1小题）
8．（2023•微山县一模）如图，A是双曲线上的一点，点C是AO的中点，过点C作y轴的垂线，垂足为D，交双曲线于点B，则△ABD的面积是 　3　．

【答案】3．
【解答】解：∵点C是AO的中点，
∴S△ACD＝S△OCD，S△ACB＝S△OCB，
∴S△ABD＝S△ACD+S△ACB＝S△OCD+S△OCB＝S△OBD，
∵点B是双曲线上一点，BD⊥OD，
∴，
∴△ABD的面积是3，
故答案为：3．
九．反比例函数图象上点的坐标特征（共1小题）
9．（2023•金乡县一模）已知点A（1，y1），B（3，y2）在反比例函数y＝的图象上，且y1＜y2，则m的取值范围是 　m＜2　．
【答案】m＜2．
【解答】解：∵1＜3时，y1＜y2，
∴在同一象限内，y随着x增大而增大，
∴m﹣2＜0，
∴m＜2，
故答案为：m＜2．
一十．抛物线与x轴的交点（共1小题）
10．（2023•金乡县一模）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（1，0）、点B与y轴相交于点C（0，3），下列结论：①b＝﹣2；②B点坐标为（﹣3，0）；③抛物线的顶点坐标为（﹣1，3）；④直线y＝h与抛物线交于点D、E，若DE＜2，则h的取值范围是3＜h＜4；⑤在抛物线的对称轴上存在一点Q，使△QAC的周长最小，则Q点坐标为（﹣1，2）．其中正确的有 　①②④⑤　．

【答案】①②④⑤．
【解答】解：①将A（1，0）、C（0，3）代入y＝﹣x2+bx+c中，
，
解得：，
∴结论①正确；
②∵y＝﹣x2﹣2x+3＝﹣（x+3）（x﹣1），
∴点B的坐标为（﹣3，0），结论②正确；
③∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴抛物线的顶点坐标为（﹣1，4），结论③不正确；
④∵抛物线的对称轴为x＝﹣1，
∴﹣1+1＝0．
当x＝0时，y＝﹣x2﹣2x+3＝3．
∵抛物线的顶点坐标为（﹣1，4），
∴直线y＝h与抛物线交于点D、E，若DE＜2，则h的取值范围是3＜h＜4，结论④正确；
⑤连接BC，交抛物线的对称轴于点Q，此时△QAC的周长最小，如图所示．
设直线BC的解析式为y＝mx+n，
将B（﹣3，0）、C（0，3）代入y＝mx+n中，
，
解得，
∴直线BC的解析式为y＝x+3．
当x＝﹣1时，y＝x+3＝2，
∴当△QAC的周长最小时，Q点坐标为（﹣1，2），结论⑤正确．
综上所述，正确的结论有：①②④⑤．
故答案为：①②④⑤．

一十一．平行线的性质（共1小题）
11．（2023•邹城市一模）如图，一条公路修到湖边时，需拐弯绕道而过，如果第一次拐的∠A＝120°，第二次拐的∠B＝150°，第三次拐的∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C＝　150°　．

【答案】150°．
【解答】解：过点B作BD∥AE，
由已知可得：AE∥CF，
∴AE∥BD∥CF，
∴∠ABD＝∠A＝120°，∠CBD+∠C＝180°，
∴∠CBD＝∠ABC﹣∠ABD＝150°﹣120°＝30°，
∴∠C＝180°﹣∠CBD＝180°﹣30°＝150°．
故答案为：150°．

一十二．矩形的性质（共1小题）
12．（2023•汶上县一模）如图，在矩形ABCD中，AB＝9，AD＝12，点E在边CD上，且CE＝4，点P是直线BC上的一个动点．若△APE是直角三角形，则CP的长为 　或或6　．

【答案】或或6．
【解答】解：若△APE是直角三角形，有以下三种情况：
①如图1，∠AEP＝90°，

∴∠AED+∠CEP＝90°，
∵四边形ABCD是矩形，
∴∠C＝∠D＝90°，
∴∠CEP+∠CPE＝90°，
∴∠AED＝∠CPE，
∴△ADE∽△ECP，
∴＝，即＝，
∴CP＝；
②如图2，∠PAE＝90°，

∵∠DAE+∠BAE＝∠BAE+∠BAP＝90°，
∴∠DAE＝∠BAP，
∵∠D＝∠ABP＝90°，
∴△ADE∽△ABP，
∴＝，即＝，
∴BP＝，
CP＝BP+BC＝；
③如图3，∠APE＝90°，设BP＝x，则PC＝12﹣x，

同理得：△ABP∽△PCE，
∴＝，即＝，
∴x1＝x2＝6，
∴BP＝6，
∴CP＝BC﹣BP＝6；
综上，BP的长是或或6．
故答案为：或或6．
一十三．垂径定理的应用（共1小题）
13．（2023•汶上县一模）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB＝12，BC＝5，则圆形镜面的直径为 　13　．

【答案】13．
【解答】解：连接AC，

∵∠ABC＝90°，且∠ABC是圆周角，
∴AC是圆形镜面的直径，
由勾股定理得：AC＝＝＝13，
故答案为：13．
一十四．圆周角定理（共1小题）
14．（2023•任城区一模）如图，AB是⊙O的直径，CD是弦（点C不与点A，点B重合，且点C与点D位于直径AB两侧），若∠AOD＝110°，则∠BCD等于 　35°　．

【答案】35°．
【解答】解：∵∠AOD＝110°，
∴∠BOD＝180°﹣∠AOD＝180°﹣110°＝70°，
∴，
故答案为：35°．
一十五．点与圆的位置关系（共1小题）
15．（2023•曲阜市一模）如图，在矩形ABCD中，AB＝4，BC＝3，动点P在矩形的内部，连接PA、PB、PC，若∠APB＝90°，则PC的最小值是 　﹣2　．

【答案】．
【解答】解：∵∠APB＝90°，
∴P在以AB为直径的⊙O上运动，如图，

∴当O、P、C三点共线时，PC最小，
∵，OP'＝2，
∴，
故答案为：．
一十六．切线的性质（共1小题）
16．（2023•金乡县一模）如图，以CD为直径的半圆与AB，AC相切于E，C两点，C，D，B三点共线，若弧DE的长为，CD＝2，则阴影部分的面积为 　﹣　．

【答案】﹣．
【解答】解：连接OE，
设∠DOE的度数为n°，
由题意得：＝π，
解得：n＝60，即∠DOE＝60°，
∴∠COE＝120°，
∵以CD为直径的半圆与AB，AC相切于E，C两点，
∴OC⊥AC，OE⊥AB，
∴∠B＝30°，
∴OB＝2OE＝2，BE＝＝＝，
∴BC＝3，
则AC＝BCtanB＝3×＝，
∴阴影部分的面积＝×3×﹣﹣×1×＝﹣，
故答案为：﹣．

一十七．扇形面积的计算（共2小题）
17．（2023•邹城市一模）如图，在△ABC，∠C＝90°，AC＝BC，斜边AB＝2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形ODE，点C在弧DE上，则图中阴影部分的面积为 　　．

【答案】．
【解答】解：连接OC，作OM⊥BC，ON⊥AC．

∵CA＝CB，∠ACB＝90°，点O为AB的中点，AB＝2，
∴OC＝AB＝1，四边形OMCN是正方形，OM＝，
则扇形FOE的面积是：＝，
∵OA＝OB，∠AOB＝90°，点D为AB的中点，
∴OC平分∠BCA，
∵OM⊥BC，ON⊥AC，
∴OM＝ON，
∵∠GOH＝∠MON＝90°，
∴∠GOM＝∠HON，
则在△OMG和△ONH中，
，
∴△OMG≌△ONH（AAS），
∴S四边形OGCH＝S四边形OMCN＝（）2＝．
则阴影部分的面积是：，
故答案为：．
18．（2023•曲阜市一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AC＝6，以点A为圆心，AC为半径画弧交AB于点D，以点B为圆心，BC为半径画弧交AB于点E，则图中阴影部分的面积是 　5π﹣6　（结果保留π）．

【答案】5π﹣6．
【解答】解：∵在Rt△ABC，∠C＝90°，∠A＝30°，AC＝6，
∴∠B＝60°，BC＝tan30°×AC＝2，
∴阴影部分的面积S＝S扇形BCE+S扇形ACD﹣S△ACB＝+﹣×6×2＝5π﹣6．
故答案为：5π﹣6．
一十八．圆锥的计算（共1小题）
19．（2023•微山县一模）如图所示，矩形纸片ABCD中，AD＝3，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作一个圆锥的侧面和底面，则AB的长为 　2　．

【答案】2．
【解答】解：∵矩形ABCD，AD＝3，正方形ABFE和矩形EFCD，分别裁出扇形ABF和半径最大的圆，恰好能作一个圆锥的侧面和底面，
∴AB＝BF＝FE＝EA，
设AB＝x，则DE＝AD﹣AE＝3﹣x，
根据题意，得，
解得x＝2．
故答案为：2．
一十九．作图—基本作图（共1小题）
20．（2023•泗水县一模）如图，在△ABC中，∠A＝30°，∠ABC＝100°，观察尺规作图的痕迹，则∠BFC的度数为 　110°　．

【答案】110°．
【解答】解：∵DE是线段AC的垂直平分线，∠A＝30°，
∴∠A＝∠ACD＝30°∵BF是∠ABC的角平分线，∠ABC＝100°，
∴，
∵∠ACB＝180°﹣∠ABC﹣∠A，
∴∠ACB＝180°﹣100°﹣30°＝50°，
∵∠BCF＝∠ACB﹣∠DCA＝50°﹣30°＝20°，
∴∠BFC＝180°﹣∠FBC﹣∠BCF＝180°﹣50°﹣20°＝110°．
故答案为：110°．
二十．轴对称-最短路线问题（共1小题）
21．（2023•济宁一模）如图，在菱形ABCD中，AB＝4，∠ABC＝60°，点P是BD上一点，点M、N分别是BC、CD上任意一点，且PM⊥BC，垂足为M，连接PM、PN，则PM+PN的最小值为 　6　．

【答案】6．
【解答】解：如图，

作EN⊥BD，交AD于E，连接PE，EM，作EF⊥BC于F，作AG⊥BC于G，
∵菱形ABCD关于BD对称，
∴点E和N关于BD对称，
∴PE＝PN，
∴PN+PM＝PE+PM≥EM≥EF，
∴当点P是EF与BD的交点时，PN+PM最小，最小值是EF的长，
在Rt△ABG中，AB＝4，∠ABC＝60°，
∴AG＝4°＝4＝6，
∴EF＝AG＝6，
∴PM+PN的最小值为：6，
故答案为：6．
二十一．相似三角形的应用（共1小题）
22．（2023•任城区一模）将一张以AB为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形（剪掉的两个直角三角形相似），剩下的是如图所示的四边形纸片ABCD，其中∠A＝90°，AB＝9，BC＝7，CD＝6，AD＝2，则剪掉的两个直角三角形的斜边长可能是①；②；③10；④，其中正确的序号是 　②③④　．

【答案】②③④．
【解答】解：∵AB2+AD2＝85＝CD2+BC2，
∴∠BCD＝90°，
由题意知，分两种情况求解，
①如图1，△DEF∽△FCB，四边形ABEF是矩形，所求两斜边为DF，BF，

∴，即，
∴，
解得，
②如图2，△DEC∽△EBF，四边形ABEF是矩形，所求两斜边为DE，BE，

∴，即，
∴，
解得，
∴剪掉的两个直角三角形的斜边长可能是，，10，15，
故答案为：②③④．
二十二．解直角三角形的应用（共1小题）
23．（2023•微山县一模）为出行方便，近日来越来越多的市民使用起了共享单车，图1为单车实物图，图2为单车示意图，AB与地面平行，点A，B，D在同一条直线上，点D，F，G在同一条直线上，坐垫C可沿射线BE方向调节．已知，∠ABE＝70°，∠EAB＝45°，车轮半径为30cm，BE＝40cm．小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适，此时CE的长约为 　24cm　．（结果精确到1cm，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈1.41）

【答案】24cm．
【解答】解：过点C作CN⊥AB，交AB于M，交地面于N，

由题意可知MN＝30cm，当CN＝90cm时，CM＝60cm，
∴在Rt△BCM中，∠ABE＝70°，
∴sin∠ABE＝sin70°＝≈0.94，
∴BC≈64cm，
∴CE＝BC﹣BE＝64﹣40＝24（cm），
故答案为：24cm．
二十三．解直角三角形的应用-方向角问题（共1小题）
24．（2023•梁山县一模）一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西65°方向向海岛C靠近．同时，从A处出发的救援船沿南偏西10°方向匀速航行．20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为　2海里/分　．

【答案】见试题解答内容
【解答】解：作CD⊥AB，
∵∠CAB＝10°+20°＝30°，∠CBA＝65°﹣20°＝45°，
∴BD＝CD＝x海里，则AD＝[20﹣x]海里，
在Rt△ACD中，＝tan30°，
则＝，
解得x＝20，
在Rt△ACD中，AC＝2×20＝40海里，
40÷20＝2海里/分．
故答案为：2海里/分．

二十四．众数（共1小题）
25．（2023•汶上县一模）为落实“双减”政策，济宁市某初中学校对学生的课外作业的时长进行了问卷调查．其中将抽查到的15名同学的作业时长统计如表，则这组数据的众数是 　70　．
作业时长（单位：分钟
50
60
70
80
90
人数（单位：人）
1
4
6
2
2
【答案】70．
【解答】解：这15名同学的作业时长中70分钟出现的次数最多，故众数是70．
故答案为：70．
二十五．概率公式（共1小题）
26．（2023•微山县一模）一个不透明的盒子中装有3个黑球和2个白球，它们除颜色不同外，其余均相同，从盒子中随机摸出一个球是黑球的概率为 　　．
【答案】．
【解答】解：根据题意，得随机摸出一个球是黑球的概率为．
故答案为：．
二十六．列表法与树状图法（共1小题）
27．（2023•邹城市一模）“红灯停，绿灯行”是我们在日常生活中必须遵守的交通规则，这样才能保障交通顺畅和行人安全．小刚每天从家骑自行车上学都经过三个路口，且每个路口只安装了红灯和绿灯，假如每个路口红灯和绿灯亮的时间相同，那么小刚从家随时出发去学校，他遇到两次红灯的概率是 　　．
【答案】．
【解答】解：画树状图如下：

由树状图可知一共有8种等可能性的结果数，其中他遇到两次红灯的结果数有3种，
∴他遇到两次红灯的概率是，
故答案为：．