山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）

这是一份山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题），共40页。试卷主要包含了两点，，点B、C在第二象限内，，交x轴于点B，，与y轴交于点C，顶点为点D等内容，欢迎下载使用。
山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）
一．反比例函数与一次函数的交点问题（共1小题）
1．（2023•济宁一模）如图，一次函数y＝ax+b的图象与反比例函数y＝的图象交于M（﹣3，1），N（1，n）两点．
（1）求这两个函数的表达式．
（2）过动点C（m，0）且垂直于x轴的直线与一次函数及反比例函数的图象分别交于D、E两点，当点E位于点D上方时，直接写出m的取值范围．

二．反比例函数综合题（共1小题）
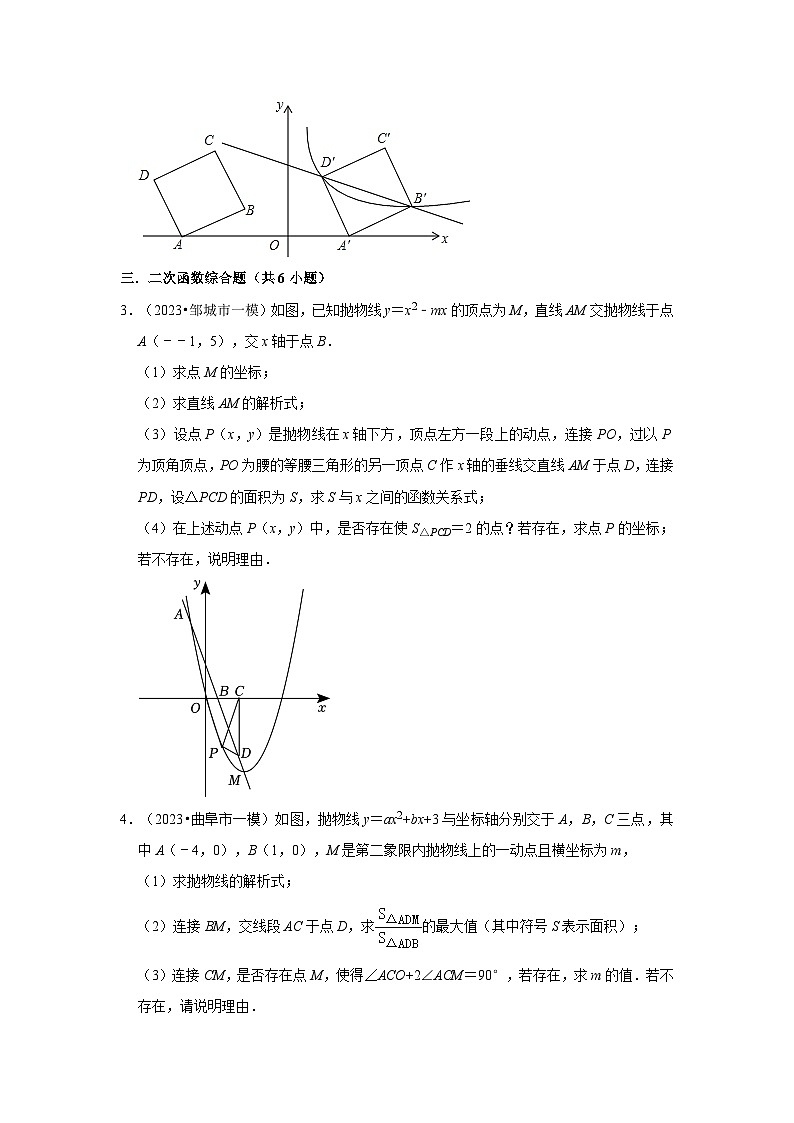
2．（2023•嘉祥县一模）如图，在平面直角坐标系中，四边形ABCD为正方形，已知点A（﹣6，0），D（﹣7，3），点B、C在第二象限内．
（1）求点B的坐标．
（2）将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒，若存在某一时刻t，使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；
（3）在（2）的情况下，问是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、B′、D′四个点为顶点的四边形是以B′D′为边的平行四边形？若存在，请直接写出符合题意的点Q的坐标；若不存在，请说明理由．

三．二次函数综合题（共6小题）
3．（2023•邹城市一模）如图，已知抛物线y＝x2﹣mx的顶点为M，直线AM交抛物线于点A（﹣﹣1，5），交x轴于点B．
（1）求点M的坐标；
（2）求直线AM的解析式；
（3）设点P（x，y）是抛物线在x轴下方，顶点左方一段上的动点，连接PO，过以P为顶角顶点，PO为腰的等腰三角形的另一顶点C作x轴的垂线交直线AM于点D，连接PD，设△PCD的面积为S，求S与x之间的函数关系式；
（4）在上述动点P（x，y）中，是否存在使S△PCD＝2的点？若存在，求点P的坐标；若不存在，说明理由．

4．（2023•曲阜市一模）如图，抛物线y＝ax2+bx+3与坐标轴分别交于A，B，C三点，其中A（﹣4，0），B（1，0），M是第二象限内抛物线上的一动点且横坐标为m，
（1）求抛物线的解析式；
（2）连接BM，交线段AC于点D，求的最大值（其中符号S表示面积）；
（3）连接CM，是否存在点M，使得∠ACO+2∠ACM＝90°，若存在，求m的值．若不存在，请说明理由．

5．（2023•任城区一模）在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．
（1）求点C的坐标和过A，B，C三点的抛物线的解析式；
（2）求点D的坐标：
（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．

6．（2023•汶上县一模）如图1，在平面直角坐标系中，抛物线与x轴交于A，B（4，0）两点，点C在y轴上，且OC＝OB，D，E分别是线段AC，AB上的动点（点D，E不与点A，B，C重合）：
（1）求此抛物线的表达式及点A的坐标；
（2）连接DE并延长交抛物线于点P，当DE⊥x轴，且AE＝1时，求DP的长；
（3）如图2，连接BD，将△BCD沿x轴翻折得到△BFG，当点G在抛物线上时，求点G的坐标．

7．（2023•金乡县一模）如图1，直线y＝﹣x+5与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴的另一交点坐标为A（﹣1，0）．

（1）求B、C两点的坐标及该抛物线所对应的函数关系式；
（2）P在线段BC上的一个动点（与B、C不重合），过点P作直线a∥y轴，交抛物线于点E，交x轴于点F，设点P的横坐标为m．
①若点P的横坐标为m，请用m表示线段PE的长度并写出m的取值范围；
②有人认为：当直线a与抛物线的对称轴重合时，线段PE的值最大，你同意他的观点吗？请说明理由；
③过点P作直线b∥x轴（图2），交AC于点Q，那么在x轴上是否存在点R，使得△PQR与△BOC相似？若存在，请求出点R的坐标；若不存在，请说明理由．

8．（2023•微山县一模）在平面直角坐标系中，抛物线y＝mx2﹣4mx+4m+6（m＜0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．

（1）当m＝﹣6时，直接写出点A，C，D的坐标；
（2）如图1，直线DC交x轴于点E，若，求m的值及直线DE的解析式；
（3）如图2，在（2）的条件下，若点Q为OC的中点，连接BQ，动点P在第一象限的抛物线上运动，过点P作x轴的垂线．垂足为H，交BQ于点M，交直线ED于点J，过点M作MN⊥DE，垂足为N．是否存在PM与MN和的最大值？若存在，求出PM与MN和的最大值；若不存在，请说明理由．
四．三角形综合题（共1小题）
9．（2023•泗水县一模）数学课上，李老师出示了如下框中的题目．
如图1，边长为6的等边三角形ABC中，点D沿线段AB方向由A向B运动，点F同时从C出发，以相同的速度沿射线BC方向运动，过点D作DE⊥AC，连接DF交射线AC于点G．求线段AC与EG的数量关系，并说明理由．

小敏与同桌小聪讨论后，进行了如下解答，：
（1）特殊情况•探索结论
当点D恰好在点B处时，易知线段AC与EG的关系是：　 　（直接写出结论）
（2）特例启发•解答题目
猜想：线段AC与EG是（1）中的关系，进行证明：
辅助线为“过点D作DH∥BC交AC于点H”，
请你利用全等三角形的相关知识完成解答；
（3）拓展结论•设计新题
如果点D运动到了线段AB的延长线上（如图2），刚才的结论是否仍成立？请你说明理由．
五．四边形综合题（共2小题）
10．（2023•曲阜市一模）（1）【证明体验】如图1，正方形ABCD中，E、F分别是边AB和对角线AC上的点，∠EDF＝45°．
①求证：△DBE∼△DCF；
②＝　 　；
（2）【思考探究】如图2，矩形ABCD中，AB＝6，BC＝8，E、F分别是边AB和对角线AC上的点，tan∠EDF＝，BE＝5，求CF的长；
（3）【拓展延伸】如图3，菱形ABCD中，BC＝5，对角线AC＝6，BH⊥AD交DA的延长线于点H，E、F分别是线段HB和AC上的点，tan∠EDF＝，HE＝，求CF的长．


11．（2023•邹城市一模）阅读与理解：如图1，是一张长2m宽1m的矩形桌球台ABCD，并且球面的摩擦力很小，现有一小球从点M（点M在边BC上）出发沿MN射向边CD的N点，然后分别反弹到AD，AB和BC上．设∠NMC＝α，如果∠1＝∠2＝3＝a，则小球仍能回到M点．
画图与计算：如果小球分别处于图2，图3中的M点，从M点射向边CD的N点，分别反弹到AD边上的P点和AB边上的Q点，然后回到M点停止．

（1）试利用正方形网格在图2，图3中分别画出小球所经过的路线图；
（2）如果图2，图3中的矩形长与宽分别为8和4，计算图2，图3中小球经过的路线长度；
探索与发现：
（3）如果点M是BC的中点，且小球经过反弹后回到出发点M，请判断小球运动路线构成什么图形？为什么？
（4）不论小球处于BC边的什么位置（顶点除外），如果小球仍能经过反弹回到出发点，小球所经过的路线长度是否为定值？如果为定值，请给予证明．
六．圆的综合题（共1小题）
12．（2023•任城区一模）对于平面直角坐标系xOy中的点M和图形G1，G2给出如下定义：点P为图形G1上一点，点Q为图形G2上一点，当点M是线段PQ的中点时，称点M是图形G1，G2的“中立点”．如果点P（x1，y1），Q（x2，y2），那么“中立点”M的坐标为（，）．已知，点A（﹣3，0），B（4，4），C（4，0）．
（1）连接BC，在点D（，0），E（0，1），F（，）中，可以成为点A和线段BC的“中立点”的是　 　；
（2）已知点G（3，0），⊙G的半径为2．如果直线y＝x﹣1上存在点K可以成为点A和⊙G的“中立点”，求点K的坐标；
（3）以点C为圆心，半径为2作圆．点N为直线y＝2x+4上的一点，如果存在点N，使得y轴上的一点可以成为点N与⊙C的“中立点”．直接写出点N的横坐标n的取值范围．

七．相似形综合题（共1小题）
13．（2023•汶上县一模）【问题呈现】
（1）如图1，△ABC和△ADE都是等边三角形，连接BD，CE，求证：BD＝CE；
【类比探究】
（2）如图2，△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°，连接BD，CE，求的值；
【拓展提升】
（3）如图3，△ABC和△ADE都是直角三角形，∠ABC＝∠ADE＝90°，且，连接BD，CE，直接写出的值．



山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）
参考答案与试题解析
一．反比例函数与一次函数的交点问题（共1小题）
1．（2023•济宁一模）如图，一次函数y＝ax+b的图象与反比例函数y＝的图象交于M（﹣3，1），N（1，n）两点．
（1）求这两个函数的表达式．
（2）过动点C（m，0）且垂直于x轴的直线与一次函数及反比例函数的图象分别交于D、E两点，当点E位于点D上方时，直接写出m的取值范围．

【答案】（1）y＝﹣；y＝﹣x﹣2；
（2）m＞1或﹣3＜m＜0．
【解答】解；（1）反比例函数y＝的图象过点M（﹣3，1），
∴k＝﹣3，
反比例函数的解析式为y＝﹣，
反比例函数y＝﹣的图象过点N（1，n），
∴n＝﹣＝﹣3，
∴N（1，﹣3），
一次函数y＝ax+b的图象过点M（﹣3，1）、N（1，﹣3），
，
解得，
故一次函数的解析式为y＝﹣x﹣2；

（2）由图象可知，m的取值范围是m＞1或﹣3＜m＜0．
二．反比例函数综合题（共1小题）
2．（2023•嘉祥县一模）如图，在平面直角坐标系中，四边形ABCD为正方形，已知点A（﹣6，0），D（﹣7，3），点B、C在第二象限内．
（1）求点B的坐标．
（2）将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒，若存在某一时刻t，使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上，请求出此时t的值以及这个反比例函数的解析式；
（3）在（2）的情况下，问是否存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、B′、D′四个点为顶点的四边形是以B′D′为边的平行四边形？若存在，请直接写出符合题意的点Q的坐标；若不存在，请说明理由．

【答案】（1）点B的坐标为（﹣3，1）；
（2）t＝9，反比例函数解析式为y＝；
（3）存在，Q的坐标为（3，2）或（﹣3，﹣2）．
【解答】解：（1）过点D作DE⊥x轴于点E，过点B作BF⊥x轴于点F，如图1所示．

∵四边形ABCD为正方形，
∴AD＝AB，∠BAD＝90°，
∵∠EAD+∠ADE＝90°，∠EAD+∠BAF＝90°，
∴∠ADE＝∠BAF．
在△ADE和△BAF中，
，
∴△ADE≌△BAF（AAS），
∴DE＝AF，AE＝BF．
∵点A（﹣6，0），D（﹣7，3），
∴DE＝3，AE＝1，
∴点B的坐标为（﹣6+3，0+1），即（﹣3，1）．
∴点B的坐标为（﹣3，1）；
（2）设反比例函数为y＝，
由题意得：点B′坐标为（﹣3+t，1），点D′坐标为（﹣7+t，3），
∵点B′和D′在该比例函数图象上，
∴，
解得：t＝9，k＝6，
∴反比例函数解析式为y＝；
（3）假设存在，设点P的坐标为（m，0），点Q的坐标为（n，）．
当B′D′为边时．
∵四边形PQB′D′为平行四边形，
∴，
解得：，
∴P（7，0），Q（3，2）；
∵四边形B′QPD′为平行四边形，
∴，
解得：，
∴P（﹣7，0），Q（﹣3，﹣2）；
综上可知：存在x轴上的点P和反比例函数图象上的点Q，使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形，符合题意的Q的坐标为（3，2）或（﹣3，﹣2）．
三．二次函数综合题（共6小题）
3．（2023•邹城市一模）如图，已知抛物线y＝x2﹣mx的顶点为M，直线AM交抛物线于点A（﹣﹣1，5），交x轴于点B．
（1）求点M的坐标；
（2）求直线AM的解析式；
（3）设点P（x，y）是抛物线在x轴下方，顶点左方一段上的动点，连接PO，过以P为顶角顶点，PO为腰的等腰三角形的另一顶点C作x轴的垂线交直线AM于点D，连接PD，设△PCD的面积为S，求S与x之间的函数关系式；
（4）在上述动点P（x，y）中，是否存在使S△PCD＝2的点？若存在，求点P的坐标；若不存在，说明理由．

【答案】（1）（2，﹣4）；
（2）y＝﹣3x+2；
（3）；
（4）存在动点P，使S△PCD＝2，此时P点坐标为（1，﹣3）．
【解答】解：（1）把A（﹣﹣1，5）代入y＝x2﹣mx中得y＝1+m＝5，
∴m＝4，
∴抛物线解析式为y＝x2﹣4x＝（x﹣2）2﹣4，
∴顶点M的坐标为（2，﹣4）；
（2）设直线AM的解析式为y＝kx+b（k≠0），
把A（﹣﹣1，5），M（2，﹣4）两点代入y＝kx+b（k≠0）得：，
解得，
∴直线AM的解析式为y＝﹣3x+2；
（3）在y＝﹣3x+2中，令y＝0，解得，
∴B点坐标为；
设P（x，x2﹣4x），
∵以PO、PC为腰的等腰三角形的另一顶点C在x轴上，
∴C的坐标是（2x，0），
∵CD⊥x轴，
∴D（2x，﹣6x+2），
∴CD＝|﹣6x+2|，
∴．
∴；
（4）当S＝2，时，则﹣3m2+m＝2，
∴3m2﹣m+2＝0，此时Δ＝1﹣4×2×3＝﹣23＜0，即方程无解，
∴此种情形不成立；
当S＝2，时，则3m2﹣m＝2，
∴3m2﹣m﹣2＝0，即（m﹣1）（3m+2）＝0，
解得m＝1或（舍去），
∴P（1，﹣3）
∴存在动点P，使S△PCD＝2，此时P点坐标为（1，﹣3）．
4．（2023•曲阜市一模）如图，抛物线y＝ax2+bx+3与坐标轴分别交于A，B，C三点，其中A（﹣4，0），B（1，0），M是第二象限内抛物线上的一动点且横坐标为m，
（1）求抛物线的解析式；
（2）连接BM，交线段AC于点D，求的最大值（其中符号S表示面积）；
（3）连接CM，是否存在点M，使得∠ACO+2∠ACM＝90°，若存在，求m的值．若不存在，请说明理由．

【答案】（1）y＝﹣x+3；（2）有最大值为；（3）存在点M，使得∠ACO+2∠ACM＝90°，此时m的值为﹣．
【解答】解：（1）∵抛物线y＝ax2+bx+3经过点A（﹣4，0），B（1，0），
∴，
解得：，
∴抛物线的解析式为y＝﹣x+3；
（2）令x＝0，则y＝3，
∴C（0，3），
设直线AC的解析式为y＝kx+c，
∴，
解得：，
∴直线AC的解析式为y＝x+3．
过点M作ME∥x轴，交直线AC于点E，如图，
∵M是第二象限内抛物线上的一动点且横坐标为m，
∴M（m，﹣﹣m+3），
∵ME∥x轴，交直线AC于点E，
∴E（﹣m2﹣3m，﹣﹣m+3），
∴ME＝（﹣m2﹣3m）﹣m＝﹣m2﹣4m，
∵A（﹣4，0），B（1，0），
∴AB＝5．
∴＝﹣．
∴＝．
∵ME∥x，
∴△MED∽△BAD，
∴＝﹣．
∵，
∴，
∵＜0，
∴当m＝﹣1时，有最大值为；
（3）存在点M，使得∠ACO+2∠ACM＝90°，此时m的值为﹣，理由：
连接CM并延长交x轴于点N，如图，
∵CO⊥OA，
∴∠N+∠NCO＝90°，
∴∠N+∠ACO+∠ACM＝90°，
∵∠ACO+2∠ACM＝90°，
∴∠ACM＝∠N，
∴AN＝AC．
∵AC＝＝＝5，
∴AN＝5，
∴ON＝OA+AN＝9，
∴N（﹣9，0）．
设直线CN的解析式为y＝nx+d，
∴，
解得：，
∴直线CN的解析式为y＝x+3．
联立：，
解得：（舍去），．
∴m＝﹣．


5．（2023•任城区一模）在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C，过点C作圆的切线交x轴于点D．
（1）求点C的坐标和过A，B，C三点的抛物线的解析式；
（2）求点D的坐标：
（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．

【答案】（1）点C的坐标为（0，2）；；
（2）点D的坐标为；
（3）存在，该圆的半径为或．
【解答】解：（1）设以AB为直径的圆的圆心为O'，连结O'C，如图．

∵A（﹣4，0），B（1，0），
∴AB＝5，
∴，
∴，
在Rt△CO'O中，，
∴点C的坐标为（0，2），
由题意，可设所求抛物线的解析式为y＝a（x﹣1）（x+4），把C（0，2）代入，
得2＝a（0﹣1）（0+4），
解得，
∴所求抛物线的解析式为，
即；
（2）∵CD为圆O'的切线，
∴O'C⊥CD，
∴∠O'CO+∠DCO＝90°．
又∵∠O'CO+∠CO'O＝90°，
∴∠DCO＝∠CO'O
∴Rt△COD∽Rt△O'OC，
∴．
即，
∴．
∴点D的坐标为．

（3）存在．
抛物线的对称轴为，
设满足条件的圆的半径为r，则点E的坐标为或，
∵点E在抛物线上，
∴，
整理得4r2+8r﹣25＝0，
解得（负值，舍去），，
或，
整理得4r2﹣8r﹣25＝0，
解得（负值，舍去），，
∴存在以线段EF为直径的圆，恰好与x轴相切，该圆的半径为或．
6．（2023•汶上县一模）如图1，在平面直角坐标系中，抛物线与x轴交于A，B（4，0）两点，点C在y轴上，且OC＝OB，D，E分别是线段AC，AB上的动点（点D，E不与点A，B，C重合）：
（1）求此抛物线的表达式及点A的坐标；
（2）连接DE并延长交抛物线于点P，当DE⊥x轴，且AE＝1时，求DP的长；
（3）如图2，连接BD，将△BCD沿x轴翻折得到△BFG，当点G在抛物线上时，求点G的坐标．

【答案】（1）y＝x2﹣x﹣3；A（﹣3，0）；
（2）DP＝；
（3）G（﹣，﹣）．
【解答】解：（1）∵抛物线y＝（x+3）（x﹣a）与x轴交于A，B（4，0）两点，
∴（4+3）（4﹣a）＝0，
解得a＝4，
∴y＝（x+3）（x﹣4）＝x2﹣x﹣3，
即抛物线的表达式为y＝x2﹣x﹣3；
当y＝0时，x＝4或﹣3；
∵A点在x轴左半轴，
∴A（﹣3，0）；
（2）在y＝（x+3）（x﹣4）中，令y＝0，得x＝﹣3或4，
∴A（﹣3，0），OA＝3，
∵OC＝OB＝4，
∴C（0，4），
∵AE＝1，
∴DE＝AE•tan∠CAO＝AE＝，OE＝OA﹣AE＝3﹣1＝2，
∴E（﹣2，0），
∵DE⊥x轴，
∴xP＝xD＝xE＝﹣2，
∴yP＝（﹣2+3）（﹣2﹣4）＝﹣，
∴PE＝，
∴DP＝DE+PE＝+＝；
（3）①如图2，连接DG交AB于点M，

∵△BCD与△BFG关于x轴对称，
∴DG⊥AB，DM＝GM，
设OM＝b（b＞0），则AM＝OA﹣OM＝3﹣b，
MG＝MD＝AM•tan∠CAO＝（3﹣b），
∴G（﹣b，（b﹣3）），
∵点G（﹣b，（b﹣3））在抛物线y＝（x+3）（x﹣4）上，
∴（﹣b+3）（﹣b﹣4）＝（b﹣3），
解得b＝或3（舍去），
∴G（﹣，﹣）．
7．（2023•金乡县一模）如图1，直线y＝﹣x+5与x轴、y轴分别交于B、C两点，经过B、C两点的抛物线与x轴的另一交点坐标为A（﹣1，0）．

（1）求B、C两点的坐标及该抛物线所对应的函数关系式；
（2）P在线段BC上的一个动点（与B、C不重合），过点P作直线a∥y轴，交抛物线于点E，交x轴于点F，设点P的横坐标为m．
①若点P的横坐标为m，请用m表示线段PE的长度并写出m的取值范围；
②有人认为：当直线a与抛物线的对称轴重合时，线段PE的值最大，你同意他的观点吗？请说明理由；
③过点P作直线b∥x轴（图2），交AC于点Q，那么在x轴上是否存在点R，使得△PQR与△BOC相似？若存在，请求出点R的坐标；若不存在，请说明理由．

【答案】（1）B（5，0）、C（0，5），y＝﹣x2+4x+5；
（2）①PE＝﹣m2+5m（0＜m＜5）；
②不同意他的观点，理由见解析；
③x轴上存在点R（﹣，0）或（，0）或（，0），使得△PQR与△BOC相似．
【解答】解：（1）在y＝﹣x+5中，令y＝0，得﹣x+5＝0，解得x＝5，
令x＝0，得y＝5，
∴B（5，0），C（0，5），
设抛物线y＝ax2+bx+c（a≠0），
∵抛物线经过点A（﹣1，0）、B（5，0）、C（0，5），
∴，
解得，
∴抛物线解析式为y＝﹣x2+4x+5；

（2）①∵点P的横坐标为m，过点P作直线a∥y轴，
∴P（m，﹣m+5），E（m，﹣m2+4m+5），
∴PE＝﹣m2+4m+5﹣（﹣m+5）＝﹣m2+4m+5+m﹣5＝﹣m2+5m，
∵P在线段BC上的一个动点（与B、C不重合），
∴0＜m＜5，
∴线段PE的长度为：PE＝﹣m2+5m（0＜m＜5）；
②不同意他的观点，理由如下：
∵PE＝﹣m2+5m＝﹣（m﹣）2+，
∴当m＝时，线段PE的值最大，
∵y＝﹣x2+4x+5的对称轴为直线x＝﹣＝2，
∴当直线a与抛物线的对称轴重合时，线段PE的值不是最大；
③∵B（5，0）、C（0，5），
∴△BOC是等腰直角三角形，
∵△PQR与△BOC相似，
∴△PQR是等腰直角三角形，
设直线AC的解析式为y＝px+t，
∵A（﹣1，0），C（0，5），

∴，解得，
直线AC的解析式为y＝5x+5，
∵点P的横坐标为m，
∴点P的纵坐标为﹣m+5，
∴点Q的纵坐标为﹣m+5，
代入直线AC得，5x+5＝﹣m+5，
解得x＝﹣，
∴PQ＝m﹣（﹣）＝m，
Ⅰ当PQ是等腰直角三角形△PQR的直角边时，

m＝﹣m+5，
解得m＝，
∴QR是直角边时，点R（﹣，0），
PR是直角边时，点R′（，0），
ⅡPQ是等腰直角三角形△PQR的斜边时，过点R作RT⊥PQ于T，

∴RT＝PT＝QT＝PQ，
∴×m＝﹣m+5，
解得m＝，
∴PQ＝m＝×＝，
OR＝m﹣PT＝﹣××＝，
∴点R（，0），
综上所述，x轴上存在点R（﹣，0）或（，0）或（，0），使得△PQR与△BOC相似．
8．（2023•微山县一模）在平面直角坐标系中，抛物线y＝mx2﹣4mx+4m+6（m＜0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．

（1）当m＝﹣6时，直接写出点A，C，D的坐标；
（2）如图1，直线DC交x轴于点E，若，求m的值及直线DE的解析式；
（3）如图2，在（2）的条件下，若点Q为OC的中点，连接BQ，动点P在第一象限的抛物线上运动，过点P作x轴的垂线．垂足为H，交BQ于点M，交直线ED于点J，过点M作MN⊥DE，垂足为N．是否存在PM与MN和的最大值？若存在，求出PM与MN和的最大值；若不存在，请说明理由．
【答案】（1）A（1，0），C（0，﹣18），D（2，6）；
（2），直线DE的解析式为；
（3）存在，PM与MN和的最大值为，理由见详解．
【解答】解：（1）把m＝﹣6代入抛物线y＝mx2﹣4mx+4m+6得y＝﹣6x2+24x﹣18，
令y＝0时，则﹣6x2+24x﹣18＝0，
则x1＝1，x2＝3，
∵点A在点B的左侧，
∴A（1，0），
令x＝0时，则y＝﹣18，即C（0，﹣18），
当时，
则y＝﹣6×4+24×2﹣18＝﹣24+48﹣18＝6，
∴D（2，6），
∴综上，点A（1，0），C（0，﹣18），D（2，6）；
（2）过点D作DF⊥BE于点F，过点C作CG⊥DF于点G，如图所示：

∴CG∥BE，
∴∠BED＝∠DCG，
∵，
∴，
由y＝mx2﹣4mx+4m+6＝m（x﹣2）2+6可知顶点D（2，6），
令x＝0时，则y＝4m+6，即C（0，4m+6），
∴DF＝6，FG＝4m+6，
∴DG＝DF﹣FG＝﹣4m，CG＝2，
∴，
解得：，
∴，
设直线DE的解析式为y＝kx+b，
则有：，
解得：，
∴直线DE的解析式为；
（3）存在，理由如下：
由（2）可知：直线DE的解析式为，，，
∴，，
令y＝0时，则，
解得：x1＝﹣1，x2＝5，
∴B（5，0），
∵点Q为OC的中点，
∴，
设直线BQ的解析式为y＝k1x+b1，
则有：，
解得：，
∴直线BQ的解析式为，
∵，JH⊥BE，
∴，即，
∴，
∴，
设，即0＜a＜5，则有，
∴，，
∴MN＝MJ•sin∠EJH＝a+1，
∴，
∵，且0＜a＜5，
综上所述，存在，当a＝3时，PM+MN有最大值，最大值即为．
四．三角形综合题（共1小题）
9．（2023•泗水县一模）数学课上，李老师出示了如下框中的题目．
如图1，边长为6的等边三角形ABC中，点D沿线段AB方向由A向B运动，点F同时从C出发，以相同的速度沿射线BC方向运动，过点D作DE⊥AC，连接DF交射线AC于点G．求线段AC与EG的数量关系，并说明理由．

小敏与同桌小聪讨论后，进行了如下解答，：
（1）特殊情况•探索结论
当点D恰好在点B处时，易知线段AC与EG的关系是：　AC＝2EG　（直接写出结论）
（2）特例启发•解答题目
猜想：线段AC与EG是（1）中的关系，进行证明：
辅助线为“过点D作DH∥BC交AC于点H”，
请你利用全等三角形的相关知识完成解答；
（3）拓展结论•设计新题
如果点D运动到了线段AB的延长线上（如图2），刚才的结论是否仍成立？请你说明理由．
【答案】见试题解答内容
【解答】解：（1）AC与EG的关系是：AC＝2EG．
理由：如图所示，当点D恰好在点B处时，点G与点C重合，

∵△ABC为等边三角形，DE⊥AH，
∴AE＝EG＝AC，
∴AC＝2EG，
故答案为：AC＝2EG；

（2）如图所示，过点D作DH∥BC，交AC于点H，则∠HDG＝∠F，

∵△ABC是等边三角形，
∴∠ADH＝∠AHD＝∠A＝60°，
∴△ADH是等边三角形，
∴AD＝DH，
又∵点D与F的运动速度相同，
∴AD＝CF，
∴DH＝FC，
在△DHG和△FCG中，
，
∴△DHG≌△FCG（AAS），
∴HG＝CG，
∵△ADH为等边三角形，DE⊥AH，
∴AE＝EH，
∴AC＝AH+CH＝2EH+2HG＝2EG；

（3）AC＝2EG仍成立，
理由：如图所示，过点D作DH∥BC，交AC的延长线于点H，则∠HDG＝∠F，

∵△ABC是等边三角形，
∴∠ADH＝∠AHD＝∠A＝60°，
∴△ADH是等边三角形，
∴AD＝DH，
又∵点D与F的运动速度相同，
∴AD＝CF，
∴DH＝FC，
在△DHG和△FCG中，
，
∴△DHG≌△FCG（AAS），
∴HG＝CG，
∵△ADH为等边三角形，DE⊥AH，
∴AE＝EH，
∴AC＝AH﹣CH＝2EH﹣2HG＝2（EH﹣HG）＝2EG．
五．四边形综合题（共2小题）
10．（2023•曲阜市一模）（1）【证明体验】如图1，正方形ABCD中，E、F分别是边AB和对角线AC上的点，∠EDF＝45°．
①求证：△DBE∼△DCF；
②＝　　；
（2）【思考探究】如图2，矩形ABCD中，AB＝6，BC＝8，E、F分别是边AB和对角线AC上的点，tan∠EDF＝，BE＝5，求CF的长；
（3）【拓展延伸】如图3，菱形ABCD中，BC＝5，对角线AC＝6，BH⊥AD交DA的延长线于点H，E、F分别是线段HB和AC上的点，tan∠EDF＝，HE＝，求CF的长．


【答案】（1）①见解析；
②；
（2）CF＝3；
（3）2．
【解答】（1）①证明：∵∠EDF＝45°，
∴∠EDB+∠BDF＝45°，
∵∠CDF+∠BDF＝45°，
∴∠EDB＝∠CDF，
∵四边形ABCD为正方形，BD，AC为对角线，
∴∠EBD＝∠FCD＝45°，
∴△DBE∼△DCF；
②解：∵四边形ABCD为正方形，BD，AC为对角线，
∴∠BDC＝45°，
∴CD＝BD•cos45°，
∴BD＝CD，
∵△DBE∽△DCF，
∴，
故答案为：；
（2）解：连接BD交AC于点O，

在矩形ABCD中，AC＝BD，
∵AB＝6，BC＝8，
∴AC＝BD＝＝10，
∴OD＝OC，
∴∠ODC＝∠OCD，
∵AB∥CD，
∴∠ABD＝∠ODC，
∴∠ABD＝∠OCD，
∵tan∠BDC＝，tan，
∴∠EDF＝∠BDC，
∵∠EDF＝∠EDB+∠BDF，∠BDC＝∠BDF+∠FDC，
∴∠EDB＝∠FDC，
∴△DBE∽△DCF，
∴，
∵BE＝5，
∴CF＝3；
（3）解：在菱形ABCD中，BC＝AB＝DC＝AD＝5，
连接BD交AC于O点，

∵AC＝BD，且AC与BD互相平分，
∴OC＝，BD＝2OD，
在Rt△ODC中，OD＝，
∴tan，
∵BD为菱形对角线，
∴∠HDB＝∠ODC，
∵BH⊥HD，AC⊥BD，
∴∠DHB＝∠DOC＝90°，
∴△DHB∽△DOC，
∴，
即，
∴BH＝，
∵HE＝，
∴BE＝BH﹣HE＝，
∵tan，
∴∠EDF＝∠ODC＝∠HDB，
∴∠EDB＝∠CDF，
∵BH⊥AD，
∴∠HBD+∠HDB＝90°，∠HDB＝∠ODC，∠ODC+∠OCD＝90°，
∴∠HBD＝∠OCD，
∴△DBE∽△DCF，
∴，
∴CF＝．
11．（2023•邹城市一模）阅读与理解：如图1，是一张长2m宽1m的矩形桌球台ABCD，并且球面的摩擦力很小，现有一小球从点M（点M在边BC上）出发沿MN射向边CD的N点，然后分别反弹到AD，AB和BC上．设∠NMC＝α，如果∠1＝∠2＝3＝a，则小球仍能回到M点．
画图与计算：如果小球分别处于图2，图3中的M点，从M点射向边CD的N点，分别反弹到AD边上的P点和AB边上的Q点，然后回到M点停止．

（1）试利用正方形网格在图2，图3中分别画出小球所经过的路线图；
（2）如果图2，图3中的矩形长与宽分别为8和4，计算图2，图3中小球经过的路线长度；
探索与发现：
（3）如果点M是BC的中点，且小球经过反弹后回到出发点M，请判断小球运动路线构成什么图形？为什么？
（4）不论小球处于BC边的什么位置（顶点除外），如果小球仍能经过反弹回到出发点，小球所经过的路线长度是否为定值？如果为定值，请给予证明．
【答案】（1）见解析；
（2）图2：；图3：；
（3）小球运动路线构成菱形，理由见解析；
（4）小球所经过的路线长度为定值，证明见解析．
【解答】（1）解：如图所示，即为所求；

（2）解：图2：由题意得，，
∴小球经过的路线长为；
图3：由题意得，，
∴小球经过的路线长为；
（3）解：小球运动路线构成菱形，理由如下：
如图1所示，∵M是BC的中点，
∴BM＝CM，
∵四边形ABCD是矩形，
∴∠B＝∠C＝∠A＝∠D＝90°，
又∵∠BMQ＝∠CMN，
∴△BMQ≌△CMN（ASA），
∴QM＝NM，
∵∠A＝∠B，∠3＝∠2，
∴∠AQP＝∠BQM，
∴∠PQM＝180°﹣∠PQA﹣∠BQM＝180°﹣2∠BQM，
同理∠QMN＝180°﹣2∠3，
∴∠PQM+∠QMN＝180°﹣2∠BQM+180°﹣2∠3＝360°﹣2（∠3+∠BQM）＝180°，
∴PQ∥MN，
同理可证PN∥QM，
∴四边形PQMN是平行四边形，
又∵QM＝NM，
∴四边形PQMN是菱形；

（4）解：小球所经过的路线长度为定值，证明如下：
如图1所示，设AB＝a，BC＝b，CM＝y，CN＝x，则BM＝b﹣y，
∵四边形PQMN是平行四边形，
∴PQ＝MN，
又∵∠A＝∠C＝90°，∠2＝∠CMN，
∴△APQ≌△CMN（AAS），
∴AQ＝CN＝x，
∴BQ＝a﹣x，
∵∠B＝∠C＝90°，∠3＝∠CMN，
∴△BMQ∽△CMN，
∴，即，
∴ay﹣xy＝bx﹣xy，
∴ay＝bx，
∴，
设，则b＝ak，y＝xk，
在Rt△CMN中，由勾股定理得，
同理可得，
∴，
∵四边形PQMN是平行四边形，
∴，
∴当矩形固定时，b和k的值都固定，则不论小球处于BC边的什么位置（顶点除外），如果小球仍能经过反弹回到出发点，小球所经过的路线长度是定值．
六．圆的综合题（共1小题）
12．（2023•任城区一模）对于平面直角坐标系xOy中的点M和图形G1，G2给出如下定义：点P为图形G1上一点，点Q为图形G2上一点，当点M是线段PQ的中点时，称点M是图形G1，G2的“中立点”．如果点P（x1，y1），Q（x2，y2），那么“中立点”M的坐标为（，）．已知，点A（﹣3，0），B（4，4），C（4，0）．
（1）连接BC，在点D（，0），E（0，1），F（，）中，可以成为点A和线段BC的“中立点”的是　D，F　；
（2）已知点G（3，0），⊙G的半径为2．如果直线y＝x﹣1上存在点K可以成为点A和⊙G的“中立点”，求点K的坐标；
（3）以点C为圆心，半径为2作圆．点N为直线y＝2x+4上的一点，如果存在点N，使得y轴上的一点可以成为点N与⊙C的“中立点”．直接写出点N的横坐标n的取值范围．

【答案】（1）D，F．
（2）点K坐标为（1，0）或（0，﹣1）．
（3）点N的横坐标的取值范围为﹣6≤xN≤﹣2．
【解答】解：（1）如图1中，

观察图象可知，满足条件的点在△ABC的平行于BC的中位线上，
故成为点A和线段BC的“中立点”的是D、F．
故答案为D、F．

（2）如图2中，点A和⊙G的“中立点”在以O为圆心，1为半径的圆上运动，

因为点K在直线y＝x﹣1上，设K（m，m﹣1），
则有m2+（m﹣1）2＝1，
解得m＝0或1，
∴点K坐标为（1，0）或（0，﹣1）．

（3）如图3中，由题意，当点N确定时，点N与⊙C的“中立点”是以NC的中点P为圆心1为半径的⊙P，
当⊙P与y轴相切时，点N的横坐标分别为﹣2或﹣6，
所以满足条件的点N的横坐标的取值范围为﹣6≤xN≤﹣2．
七．相似形综合题（共1小题）
13．（2023•汶上县一模）【问题呈现】
（1）如图1，△ABC和△ADE都是等边三角形，连接BD，CE，求证：BD＝CE；
【类比探究】
（2）如图2，△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°，连接BD，CE，求的值；
【拓展提升】
（3）如图3，△ABC和△ADE都是直角三角形，∠ABC＝∠ADE＝90°，且，连接BD，CE，直接写出的值．


【答案】（1）证明见解答过程；
（2）；
（3）．
【解答】（1）证明：∵△ABC和△ADE都是等边三角形，
∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，
∴∠BAC﹣∠BAE＝∠DAE﹣∠BAE，
即∠CAE＝∠BAD．
∴△BAD≌△CAE（SAS），
∴BD＝CE；

（2）解：∵△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°，
∴∠BAC＝∠DAE＝45°，
∴△ABC∽△ADE，
∴＝，
∴＝，
∵∠BAC＝∠DAE，
∴∠BAC﹣∠BAE＝∠DAE﹣∠BAE，
即∠CAE＝∠BAD，
∴△ADB∽△AEC，
∴＝，
设AB＝x，则BC＝x，
在Rt△ABC中，由勾股定理得，AC＝x，
∴＝＝＝；

（3）∵＝＝，∠ABC＝∠ADE＝90°，
∴△ABC∽△ADE，
∴∠BAC＝∠DAE，＝＝，
∵∠CAE＝∠BAD，
∴△CAE∽△BAD，
∴＝＝．