山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（提升题）

这是一份山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（提升题），共19页。试卷主要包含了如图，△ABC中，BA＝BC，【材料】等内容，欢迎下载使用。

山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（提升题）
一．反比例函数与一次函数的交点问题（共1小题）
1．（2023•泗水县一模）如图，一次函数y＝kx+b的图象与反比例函数的图象交于A（3，4），B（n，﹣1）．

（1）求反比例函数和一次函数的解析式；
（2）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．
二．二次函数的应用（共2小题）
2．（2023•曲阜市一模）鱼卷是非常著名的小吃之一，小张从事鱼卷批发多年，2020年小张的一位“熟客”向小张采购了500箱鱼卷，2022年这位“熟客”采购了720箱．
（1）求小张的这位“熟客”这两年向小张采购鱼卷的年平均增长率；
（2）2022年小张的这位“熟客”采购鱼卷的数量占小张总销售量的，由于鱼卷受到游客们的青睐，小张决定2023年在网上出售鱼卷，若没有在网上出售鱼卷，则按去年的价格出售，每箱利润为15元，预计总销售量与去年持平；若计划在网上出售鱼卷，则需把每箱售价下调4至5元，且每下调1元销售量可增加100箱，预计小张在2023年能获得的最大利润是多少元？
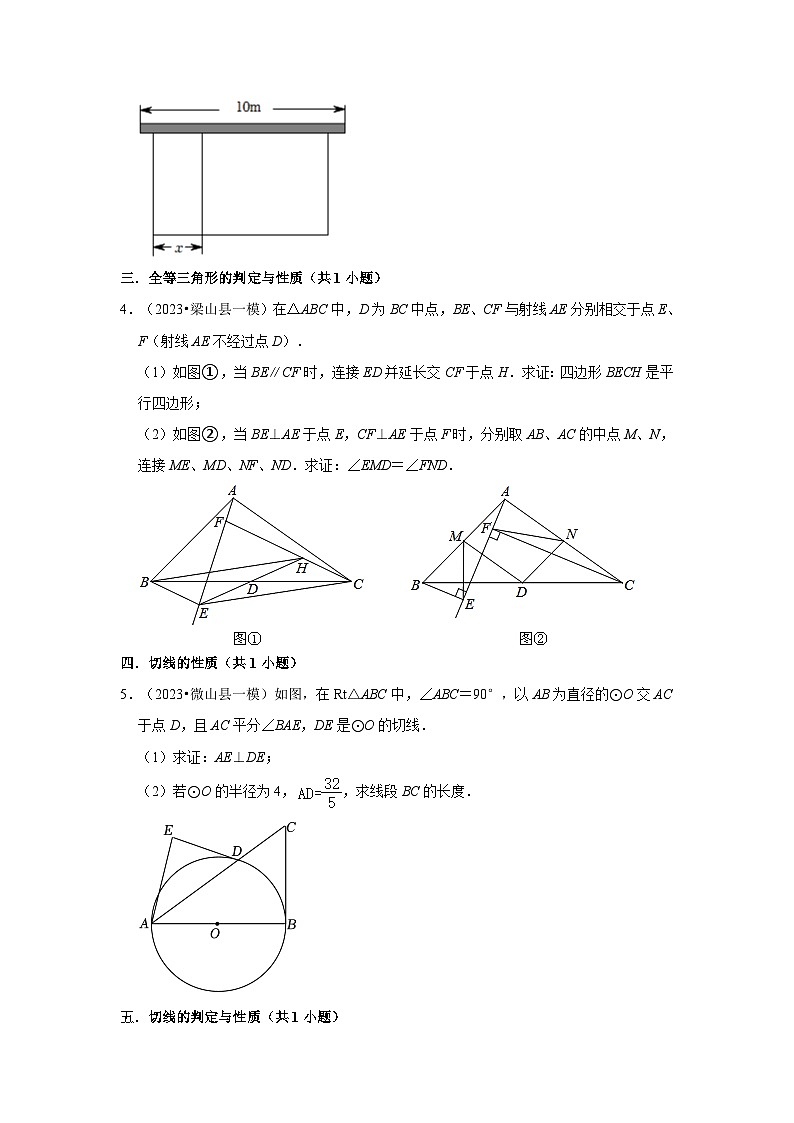
3．（2023•汶上县一模）某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）．
（1）若矩形养殖场的总面积为36m2，求此时x的值；
（2）当x为多少时，矩形养殖场的总面积最大？最大值为多少？

三．全等三角形的判定与性质（共1小题）
4．（2023•梁山县一模）在△ABC中，D为BC中点，BE、CF与射线AE分别相交于点E、F（射线AE不经过点D）．
（1）如图①，当BE∥CF时，连接ED并延长交CF于点H．求证：四边形BECH是平行四边形；
（2）如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND．求证：∠EMD＝∠FND．

四．切线的性质（共1小题）
5．（2023•微山县一模）如图，在Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，且AC平分∠BAE，DE是⊙O的切线．
（1）求证：AE⊥DE；
（2）若⊙O的半径为4，，求线段BC的长度．

五．切线的判定与性质（共1小题）
6．（2023•曲阜市一模）如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D，交CA的
延长线于点E，连接BE，过点D作DF⊥AC，垂足为点F．
（1）求证：DF是⊙O的切线；
（2）如果DF＝6，AE＝5，求⊙O的半径．

六．作图—复杂作图（共2小题）
7．（2023•微山县一模）如图，△ABC中，BA＝BC．
（1）读下列语句，完成作图（要求：尺规作图，保留作图痕迹，不写作法）：
①过点A作AE∥BC；
②在AE上取一点D（点D在点A的右侧），使点D到边BA，BC所在直线的距离相等．
（2）若AB＝13，AC＝10，求点A到BC的距离．

8．（2023•嘉祥县一模）【材料】
《义务教育数学课程标准2022版）》对《切线的性质与判定》的新要求是：切线长定理由“选学”改为“必学”，并新增“能用尺规作图：过圆外的一个点作圆的切线（课标课程内容中的实例76）．根据这一要求转化为作图题为：

已知：如图，⊙O及⊙O外一点P
求作：过点P的⊙O的切线
作法：
①连接OP，作线段OP的垂直平分线MN交OP于点T；
②以点T为圆心，TP的长为半径作圆，交⊙O于点A、点B；
③作直线PA，PB．
则直线PA，PB就是所求作的⊙O的切线．
【问题】
（1）请你按照上述步骤完成作图（尺规作图，保留作图痕迹）；
（2）完成下面的证明．
证明：连接OA．
∵OP是⊙T的直径，
∴∠OAP＝　 　°． 　 　（填推理的依据）．
∴OA⊥AP．
又∵OA为⊙O的半径，
∴直线PA是⊙O的切线 　 　（填推理的依据）．
同理可证，直线PB也是⊙O的切线．
（3）在（2）的条件下，连接AT，若∠APB＝30°，△AOT的面积等于1，求⊙T的半径．
七．解直角三角形的应用-仰角俯角问题（共1小题）
9．（2023•汶上县一模）如图，为测量某大楼CD顶部广告牌DE的高度，在距离大楼30m的A处用测角仪器测得∠DAC＝30°；从A处向大楼方向走10m到达B处，测得∠EBC＝48°．已知测角仪器的高度忽略不计，求广告牌DE的高度．（结果保留小数点后一位）
（参考数据：≈1.732，sin48°≈0.743，cos48°≈0.669，tan48°≈1.111）

八．列表法与树状图法（共1小题）
10．（2023•微山县一模）某市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一外型、型号、颜色等．其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶．为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机调查了部分学生，并根据调查结果，绘制了如图所示的两幅不完整的统计图．

根据图中信息，解答下列问题：
（1）此次共随机调查了 　 　名学生，扇形统计图中“红“所在扇形的圆心角的度数为 　 　度，补全条形统计图（要求在条形图上方注明人数）；
（2）若该校有2000名学生，估计该校学生将用过的餐巾纸投放到灰色收集桶的人数；
（3）李老师计划从A，B，C，D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图或列表法求出恰好抽中C，D两人的概率．

山东省济宁市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（提升题）
参考答案与试题解析
一．反比例函数与一次函数的交点问题（共1小题）
1．（2023•泗水县一模）如图，一次函数y＝kx+b的图象与反比例函数的图象交于A（3，4），B（n，﹣1）．

（1）求反比例函数和一次函数的解析式；
（2）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．
【答案】（1），；
（2）﹣12＜x＜0或x＞3．
【解答】解：（1）∵反比例的图象过点A（3，4），
即，
∴m＝12，
∴反比例函数的解析式为，
∵点B（n，﹣1）在函数的图象上，
∴，n＝﹣12，
∴B（﹣12，﹣1），
∵一次函数y＝kx+b过A（3，4）、B（﹣12，﹣1）两点，
即，
解得，
∴一次函数的解析式为；
（2）由图象可知：当﹣12＜x＜0或x＞3时，一次函数的值大于反比例函数的值．
二．二次函数的应用（共2小题）
2．（2023•曲阜市一模）鱼卷是非常著名的小吃之一，小张从事鱼卷批发多年，2020年小张的一位“熟客”向小张采购了500箱鱼卷，2022年这位“熟客”采购了720箱．
（1）求小张的这位“熟客”这两年向小张采购鱼卷的年平均增长率；
（2）2022年小张的这位“熟客”采购鱼卷的数量占小张总销售量的，由于鱼卷受到游客们的青睐，小张决定2023年在网上出售鱼卷，若没有在网上出售鱼卷，则按去年的价格出售，每箱利润为15元，预计总销售量与去年持平；若计划在网上出售鱼卷，则需把每箱售价下调4至5元，且每下调1元销售量可增加100箱，预计小张在2023年能获得的最大利润是多少元？
【答案】（1）小张的“熟客”这两年向小张采购鱼卷的年平均增长率为20%；
（2）小张在2023年能获得的最大利润是14300元．
【解答】解：（1）设小张的“熟客”这两年向小张采购鱼卷的年平均增长率为a，
则500（1+a）2＝720，
整理得：，
解得（负根不合题意舍去）．
答：小张的“熟客”这两年向小张采购鱼卷的年平均增长率为20%．
（2）由题意，得，
解：2022年小张年总销量为（箱），
设2023年总利润为w元，价格下调x元，
则w＝（15﹣x）（900+100x）＝﹣100x2+600x+13500＝﹣100（x﹣3）2+14400，
∵a＝﹣100＜0，4≤x≤5，
∴x＝4时，w有最大值，最大值为14300．
所以小张在2023年能获得的最大利润是14300元．
3．（2023•汶上县一模）某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）．
（1）若矩形养殖场的总面积为36m2，求此时x的值；
（2）当x为多少时，矩形养殖场的总面积最大？最大值为多少？

【答案】（1）x的值为2m；（2）当时，矩形养殖场的总面积最大，最大值为m2．
【解答】解：（1）如图：

∵BC＝x，矩形CDEF的面积是矩形BCFA面积的2倍，
∴CD＝2x，
∴BD＝3x，AB＝CF＝DE＝（24﹣BD）＝8﹣x，
依题意得：3x（8﹣x）＝36，
解得：x1＝2，x2＝6（不合题意，舍去），
答：此时x的值为2m．
（2）设矩形养殖场的总面积为S，
由（1）得：S＝3x（8﹣x）＝﹣3（x﹣4）2+48，
∵墙的长度为10，
∴0＜3x＜10，
∴0＜x＜，
∵﹣3＜0，
∴x＜4时，S随着x的增大而增大，
∴当x＝时，S有最大值，最大值为（m2）．
答：当时，矩形养殖场的总面积最大，最大值为m2．
三．全等三角形的判定与性质（共1小题）
4．（2023•梁山县一模）在△ABC中，D为BC中点，BE、CF与射线AE分别相交于点E、F（射线AE不经过点D）．
（1）如图①，当BE∥CF时，连接ED并延长交CF于点H．求证：四边形BECH是平行四边形；
（2）如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND．求证：∠EMD＝∠FND．

【答案】见试题解答内容
【解答】证明：（1）如图①，∵D为BC的中点，
∴BD＝CD，
∵BE∥CF，
∴∠DBE＝∠DCH，
在△BDE与△CDH中，
，
∴△BDE≌△CDH（AAS），
∴ED＝HD，
∴四边形BECH是平行四边形；

（2）如图②连接FD、ED，延长ED交CF于点H，
∵BE⊥AE，CF⊥AE，
∴BE∥CF，
由（1）可知ED＝HD，又∵CF⊥AE，
∴ED＝FD（直角三角形斜边的中线等于斜边的一半），
∵在RT△AEB中，M是AB的中点，
∴ME＝AB，
∵在△ABC中，D、N分别是BC、AC的中点，
∴DN＝AB，
∴ME＝DN，
同理，MD＝NF，
在△MED与△NDF中，
，
∴△MED≌△NDF（SSS），
∴∠EMD＝∠FND．


四．切线的性质（共1小题）
5．（2023•微山县一模）如图，在Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，且AC平分∠BAE，DE是⊙O的切线．
（1）求证：AE⊥DE；
（2）若⊙O的半径为4，，求线段BC的长度．

【答案】（1）见详解；
（2）6．
【解答】（1）证明：连接OD，如图所示：

∵DE是⊙O的切线，
∴∠ODE＝90°，
∵OA＝OD，
∴∠OAD＝∠ADO，
∵AC平分∠BAE，
∴∠OAD＝∠DAE，
∴∠DAE＝∠ADO，
∴AE∥OD，
∴∠E+∠ODE＝180°，
∴∠E＝90°，即AE⊥DE；

（2）解：连接BD，如图所示，
∵AB为⊙O的直径，
∴∠ADB＝90°，
∵⊙O的半径为4，，即AB＝8，
∴，
∴，
在Rt△ABC中，BC＝AB•tan∠BAC＝6．
五．切线的判定与性质（共1小题）
6．（2023•曲阜市一模）如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D，交CA的
延长线于点E，连接BE，过点D作DF⊥AC，垂足为点F．
（1）求证：DF是⊙O的切线；
（2）如果DF＝6，AE＝5，求⊙O的半径．

【答案】（1）见解析；
（2）⊙O的半径为．
【解答】（1）证明：连接OD，
∵AB＝AC，
∴∠B＝∠C，
∵OB＝OD，
∴∠B＝∠ODB，
∴∠C＝∠ODB，
∴OD∥AC，
∵DF⊥AC，
∴DF⊥OD，
∵OD是⊙O的半径，
∴DF是⊙O的切线；
（2）解：连接AD，
∵AB为⊙O直径，
∴∠BEA＝∠ADB＝90°，
∴∠BEA＝∠DFC，
∴BE∥DF，
∵AB＝AC，
∴BD＝CD，
∴CF＝EF，
∴DF是△BCE的中位线，
∴BE＝2DF＝12，
∵AE＝5，
∴AB＝＝13，
∴⊙O的半径为．

六．作图—复杂作图（共2小题）
7．（2023•微山县一模）如图，△ABC中，BA＝BC．
（1）读下列语句，完成作图（要求：尺规作图，保留作图痕迹，不写作法）：
①过点A作AE∥BC；
②在AE上取一点D（点D在点A的右侧），使点D到边BA，BC所在直线的距离相等．
（2）若AB＝13，AC＝10，求点A到BC的距离．

【答案】（1）①见解析；②见解析；
（2）．
【解答】解：（1）①根据尺规作图画图如下：则AE即为所求．

②过点A作AG⊥BC于点G，在①中的作图上，作AM＝BG，AD＝BA，

在△AMD和△BGA中，
，
∴△AMD≌△BGA（SAS），
∴DM＝AG，∠DMA＝∠AGB＝90°，画图如下，
则点D即为所求．

（2）如图，过点B作BF⊥AC于点F，过点A作AG⊥BC于点G，

∵AB＝13＝BC，AC＝10，
∴，
∴，
∵，
∴12×10＝13AG，
解得．
故点A到BC的距离是．
8．（2023•嘉祥县一模）【材料】
《义务教育数学课程标准2022版）》对《切线的性质与判定》的新要求是：切线长定理由“选学”改为“必学”，并新增“能用尺规作图：过圆外的一个点作圆的切线（课标课程内容中的实例76）．根据这一要求转化为作图题为：

已知：如图，⊙O及⊙O外一点P
求作：过点P的⊙O的切线
作法：
①连接OP，作线段OP的垂直平分线MN交OP于点T；
②以点T为圆心，TP的长为半径作圆，交⊙O于点A、点B；
③作直线PA，PB．
则直线PA，PB就是所求作的⊙O的切线．
【问题】
（1）请你按照上述步骤完成作图（尺规作图，保留作图痕迹）；
（2）完成下面的证明．
证明：连接OA．
∵OP是⊙T的直径，
∴∠OAP＝　90　°． 　直径所对的圆周角是直角　（填推理的依据）．
∴OA⊥AP．
又∵OA为⊙O的半径，
∴直线PA是⊙O的切线 　过半径的外端且垂直于这条半径的直线是圆的切线　（填推理的依据）．
同理可证，直线PB也是⊙O的切线．
（3）在（2）的条件下，连接AT，若∠APB＝30°，△AOT的面积等于1，求⊙T的半径．
【答案】（1）详见解答；
（2）直径所对的圆周角是直角；过半径的外端且垂直于这条半径的直线是圆的切线；
（3）2．
【解答】（1）解：作法：①连接OP，作线段OP的垂直平分线MN交OP于点T；
②以点T为圆心，TP的长为半径作圆，交⊙O于点A、点B；
③作直线PA，PB，
则直线PA，PB就是所求作的⊙O的切线；
（2）证明：连接OA．
∵OP是⊙T的直径，
∴∠OAP＝90°（直径所对的圆周角是直角）．
∴OA⊥AP，
又∵OA为⊙O的半径，
∴直线PA是⊙O的切线 （过半径的外端且垂直于这条半径的直线是圆的切线）．
同理可证，直线PB也是⊙O的切线；
故答案为：直径所对的圆周角是直角；过半径的外端且垂直于这条半径的直线是圆的切线；
（3）解：过点A作AC⊥OP，垂足为C，
∵PA、PB是⊙T的切线，点A、点B是切点，
∴∠APO＝∠BPO＝∠APB＝15°，
又∵TA＝TP，
∴∠TAP＝∠TPA＝15°，
∴∠ATO＝2∠TAP＝30°，
在Rt△ACT中，AC＝TA，
由三角形面积公式可得，
S△AOT＝OT•AC＝1，
即OT2＝1，
∴OT＝2，
即⊙T的半径为2．

七．解直角三角形的应用-仰角俯角问题（共1小题）
9．（2023•汶上县一模）如图，为测量某大楼CD顶部广告牌DE的高度，在距离大楼30m的A处用测角仪器测得∠DAC＝30°；从A处向大楼方向走10m到达B处，测得∠EBC＝48°．已知测角仪器的高度忽略不计，求广告牌DE的高度．（结果保留小数点后一位）
（参考数据：≈1.732，sin48°≈0.743，cos48°≈0.669，tan48°≈1.111）

【答案】4.9米．
【解答】解：在Rt△ADC中，∠DAC＝30°，AC＝30米，
∴CD＝AC•tan30°＝30×＝10（米），
∵AB＝10米，
∴BC＝AC﹣AB＝20（米），
在Rt△BCE中，∠EBC＝48°，
∴EC＝BC•tan48°≈20×1.111＝22.22（米），
∴DE＝EC﹣DC＝22.22﹣10≈4.9（米），
∴广告牌ED的高度约为4.9米．
八．列表法与树状图法（共1小题）
10．（2023•微山县一模）某市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一外型、型号、颜色等．其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶．为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机调查了部分学生，并根据调查结果，绘制了如图所示的两幅不完整的统计图．

根据图中信息，解答下列问题：
（1）此次共随机调查了 　200　名学生，扇形统计图中“红“所在扇形的圆心角的度数为 　28.8　度，补全条形统计图（要求在条形图上方注明人数）；
（2）若该校有2000名学生，估计该校学生将用过的餐巾纸投放到灰色收集桶的人数；
（3）李老师计划从A，B，C，D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图或列表法求出恰好抽中C，D两人的概率．
【答案】（1）200，28.8°，见解析；
（2）1100；
（3）．
【解答】解：（1）∵44÷22%＝200（人），
∴，
故答案为：200，28.8．
∴绿色的人数为：200﹣110﹣44﹣16＝30（人），补图如下：
．
（2）该校学生将用过的餐巾纸投放到灰色收集桶的人数：（人）．
（3）画树状图如下：

∴抽中C，D两人的概率是．