山东省青岛市2021-2023三年中考数学真题分类汇编-02填空题知识点分类

这是一份山东省青岛市2021-2023三年中考数学真题分类汇编-02填空题知识点分类，共18页。试卷主要包含了2＝　 　，×＝　 　，之间的反比例函数关系如图所示等内容，欢迎下载使用。
山东省青岛市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
一．绝对值（共1小题）
1．（2022•青岛）﹣的绝对值是 　 　．
二．整式的除法（共1小题）
2．（2023•青岛）计算：8x3y÷（2x）2＝　 　．
三．二次根式的混合运算（共1小题）
3．（2021•青岛）计算：（+）×＝　 　．
四．由实际问题抽象出分式方程（共2小题）
4．（2023•青岛）某校组织学生进行劳动实践活动，用1000元购进甲种劳动工具，用2400元购进乙种劳动工具，乙种劳动工具购买数量是甲种的2倍，但单价贵了4元．设甲种劳动工具单价为x元，则x满足的分式方程为 　 　．
5．（2022•青岛）为落实青岛市中小学生“十个一”行动计划，学校举办以“强体质，炼意志”为主题的体育节，小亮报名参加3000米比赛项目，经过一段时间训练后，比赛时小亮的平均速度比训练前提高了25%，少用3分钟跑完全程，设小亮训练前的平均速度为x米/分，那么x满足的分式方程为 　 　．
五．待定系数法求反比例函数解析式（共1小题）
6．（2023•青岛）反比例函数y＝的图象经过点A（m，），则反比例函数的表达式为 　 　．
六．反比例函数的应用（共1小题）
7．（2021•青岛）车从甲地驶往乙地，行完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的反比例函数关系如图所示．若列车要在2.5h内到达，则速度至少需要提高到 　 　km/h．

七．二次函数图象与系数的关系（共1小题）
8．（2023•青岛）如图，二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，已知点A的横坐标为﹣3，点B的横坐标为2，二次函数图象的对称轴是直线x＝﹣1．下列结论：①abc＜0；②3b+2c＞0；③关于x的方程ax2+bx+c＝kx的两根为x1＝﹣3，x2＝2；④k＝a．其中正确的是 　 　.（只填写序号）

八．菱形的性质（共1小题）
9．（2022•青岛）图①是艺术家埃舍尔的作品，他将数学与绘画完美结合，在平面上创造出立体效果．图②是一个菱形，将图②截去一个边长为原来一半的菱形得到图③，用图③镶嵌得到图④，将图④着色后，再次镶嵌便得到图①，则图④中∠ABC的度数是 　 　°．

九．切线的性质（共2小题）
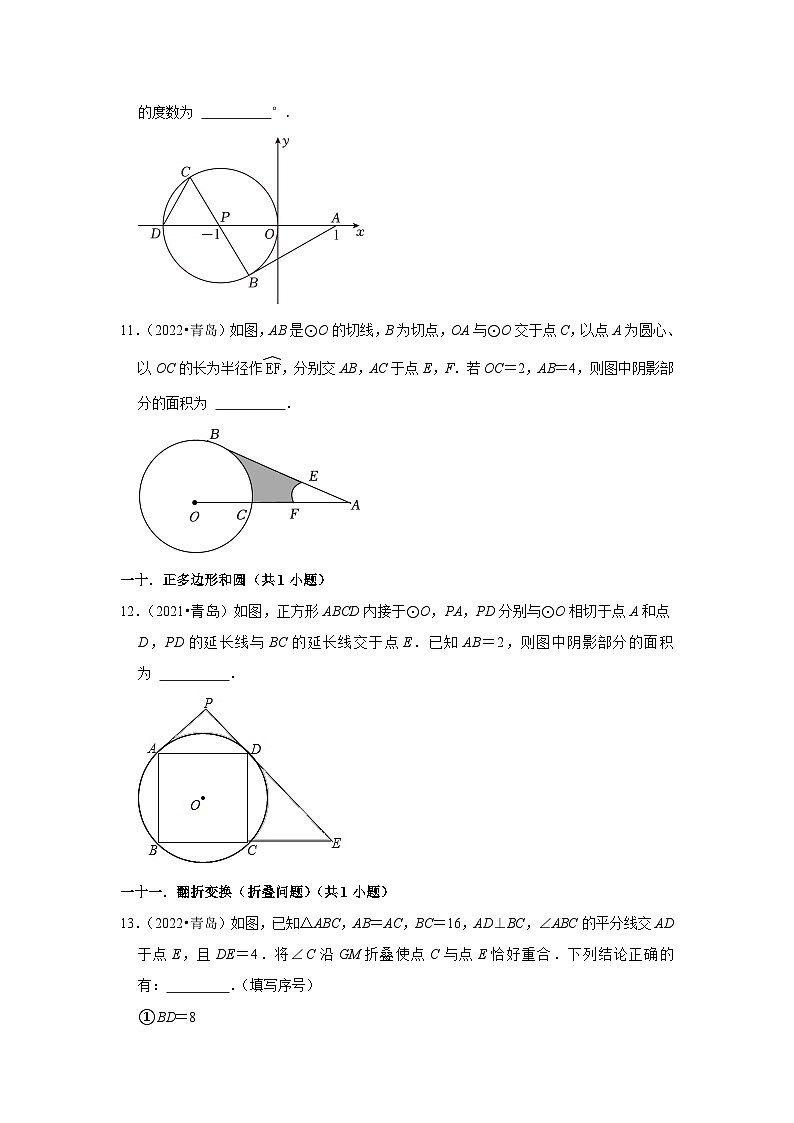
10．（2023•青岛）如图，在平面直角坐标系中，已知点A（1，0），P（﹣1，0），⊙P过原点O，且与x轴交于另一点D，AB为⊙P的切线，B为切点，BC是⊙P的直径，则∠BCD的度数为 　 　°．

11．（2022•青岛）如图，AB是⊙O的切线，B为切点，OA与⊙O交于点C，以点A为圆心、以OC的长为半径作，分别交AB，AC于点E，F．若OC＝2，AB＝4，则图中阴影部分的面积为 　 　．

一十．正多边形和圆（共1小题）
12．（2021•青岛）如图，正方形ABCD内接于⊙O，PA，PD分别与⊙O相切于点A和点D，PD的延长线与BC的延长线交于点E．已知AB＝2，则图中阴影部分的面积为 　 　．

一十一．翻折变换（折叠问题）（共1小题）
13．（2022•青岛）如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4．将∠C沿GM折叠使点C与点E恰好重合．下列结论正确的有：　 　．（填写序号）
①BD＝8
②点E到AC的距离为3
③EM＝
④EM∥AC

一十二．相似三角形的判定与性质（共1小题）
14．（2021•青岛）已知正方形ABCD的边长为3，E为CD上一点，连接AE并延长，交BC的延长线于点F，过点D作DG⊥AF，交AF于点H，交BF于点G，N为EF的中点，M为BD上一动点，分别连接MC，MN．若，则MN+MC的最小值为 　 　．

一十三．用样本估计总体（共1小题）
15．（2021•青岛）在一个不透明的袋中装有若干个红球和4个黑球，每个球除颜色外完全相同，摇匀后从中摸出一个球，记下颜色后再放回袋中，不断重复这一过程，共摸球100次，其中有40次摸到黑球，估计袋中红球的个数是 　 　．
一十四．条形统计图（共1小题）
16．（2021•青岛）已知甲、乙两队员射击的成绩如图，设甲、乙两队员射击成绩的方差分别为S甲2、S乙2，则S甲2　 　S乙2（填“＞”、“＝”、“＜”）．

一十五．加权平均数（共1小题）
17．（2022•青岛）小明参加“建团百年，我为团旗添光彩”主题演讲比赛，其演讲形象、内容、效果三项分别是9分、8分、8分．若将三项得分依次按3：4：3的比例确定最终成绩，则小明的最终比赛成绩为 　 　分．
一十六．极差（共1小题）
18．（2023•青岛）小颖参加“歌唱祖国”歌咏比赛，六位评委对小颖的打分（单位：分）如下：7，8，7，9，8，10．这六个分数的极差是 　 　分．

山东省青岛市2021-2023三年中考数学真题分类汇编-02填空题知识点分类
参考答案与试题解析
一．绝对值（共1小题）
1．（2022•青岛）﹣的绝对值是 　　．
【答案】见试题解答内容
【解答】解：|﹣|＝．
故本题的答案是．
二．整式的除法（共1小题）
2．（2023•青岛）计算：8x3y÷（2x）2＝　2xy　．
【答案】2xy．
【解答】解：原式＝8x3y÷4x2
＝2xy，
故答案为：2xy．
三．二次根式的混合运算（共1小题）
3．（2021•青岛）计算：（+）×＝　5　．
【答案】5．
【解答】解：原式＝+
＝4+1
＝5．
故答案为5．
四．由实际问题抽象出分式方程（共2小题）
4．（2023•青岛）某校组织学生进行劳动实践活动，用1000元购进甲种劳动工具，用2400元购进乙种劳动工具，乙种劳动工具购买数量是甲种的2倍，但单价贵了4元．设甲种劳动工具单价为x元，则x满足的分式方程为 　＝2×　．
【答案】＝2×．
【解答】解：∵乙种劳动工具的单价比甲种劳动工具的单价贵了4元，且甲种劳动工具单价为x元，
∴乙种劳动工具单价为（x+4）元．
根据题意得：＝2×．
故答案为：＝2×．
5．（2022•青岛）为落实青岛市中小学生“十个一”行动计划，学校举办以“强体质，炼意志”为主题的体育节，小亮报名参加3000米比赛项目，经过一段时间训练后，比赛时小亮的平均速度比训练前提高了25%，少用3分钟跑完全程，设小亮训练前的平均速度为x米/分，那么x满足的分式方程为 　﹣＝3　．
【答案】﹣＝3．
【解答】解：依题意有：﹣＝3．
故答案为：﹣＝3．
五．待定系数法求反比例函数解析式（共1小题）
6．（2023•青岛）反比例函数y＝的图象经过点A（m，），则反比例函数的表达式为 　y＝　．
【答案】y＝．
【解答】解：∵反比例函数y＝的图象经过点A（m，），
∴＝m．
∴m＝8，
∴反比例函数解析式为：y＝．
六．反比例函数的应用（共1小题）
7．（2021•青岛）车从甲地驶往乙地，行完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的反比例函数关系如图所示．若列车要在2.5h内到达，则速度至少需要提高到 　240　km/h．

【答案】240．
【解答】解：∵从甲地驶往乙地的路程为200×3＝600（km），
∴汽车行驶完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的关系式为t＝，
当t＝2.5h时，即2.5＝，
∴v＝240，
答：列车要在2.5h内到达，则速度至少需要提高到240km/h．
故答案为：240．
七．二次函数图象与系数的关系（共1小题）
8．（2023•青岛）如图，二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，已知点A的横坐标为﹣3，点B的横坐标为2，二次函数图象的对称轴是直线x＝﹣1．下列结论：①abc＜0；②3b+2c＞0；③关于x的方程ax2+bx+c＝kx的两根为x1＝﹣3，x2＝2；④k＝a．其中正确的是 　①③　.（只填写序号）

【答案】①③．
【解答】解：由图象可得，a＞0，c＜0，又﹣＝﹣1，
∴b＞0．
∴abc＜0．
∴①正确．
由题意，令ax2+bx+c＝kx，
∴ax2+（b﹣k）x+c＝0．
又二次函数y＝ax2+bx+c的图象与正比例函数y＝kx的图象相交于A，B两点，已知点A的横坐标为﹣3，点B的横坐标为2，
∴ax2+（b﹣k）x+c＝0的两根之和为﹣3+2＝﹣1，两根之积为﹣3×2＝﹣6．
∴﹣＝﹣1，＝﹣6．
∴6a+c＝0．
又b＝2a，
∴3b+c＝0．
∴3b+2c＝c＜0．
∴②错误，③正确．
∵﹣＝﹣1，b＝2a，
∴k＝a．
∴④错误．
故答案为：①③．
八．菱形的性质（共1小题）
9．（2022•青岛）图①是艺术家埃舍尔的作品，他将数学与绘画完美结合，在平面上创造出立体效果．图②是一个菱形，将图②截去一个边长为原来一半的菱形得到图③，用图③镶嵌得到图④，将图④着色后，再次镶嵌便得到图①，则图④中∠ABC的度数是 　60　°．

【答案】见试题解答内容
【解答】解：如图，

∵∠BAD＝∠BAE＝∠DAE，∠BAD+∠BAE+∠DAE＝360°，
∴∠BAD＝∠BAE＝∠DAE＝120°，
∵BC∥AD，
∴∠ABC＝180°﹣120°＝60°，
故答案为：60．
九．切线的性质（共2小题）
10．（2023•青岛）如图，在平面直角坐标系中，已知点A（1，0），P（﹣1，0），⊙P过原点O，且与x轴交于另一点D，AB为⊙P的切线，B为切点，BC是⊙P的直径，则∠BCD的度数为 　60°　°．

【答案】60°．
【解答】解：∵点A（1，0），P（﹣1，0），
∴OP＝OA＝1，
∴AP＝OP+OA＝2
∵⊙P过原点O，
∴OP为⊙P的半径，
∵AB为⊙P的切线，
∴PB⊥AB，PB＝OP＝1，
在Rt△ABP中，BP＝1，AP＝2，sinA＝PB/AP＝1/2，
∴∠BAP＝30°，
∴∠BPA＝60°，
∴∠CPD＝60°，
又∵PC＝PD，
∴三角形CPD为等边三角形，
∴∠PCD＝60°，
即∠BCD的度数为60°．
故答案为：60°．
11．（2022•青岛）如图，AB是⊙O的切线，B为切点，OA与⊙O交于点C，以点A为圆心、以OC的长为半径作，分别交AB，AC于点E，F．若OC＝2，AB＝4，则图中阴影部分的面积为 　4﹣π　．

【答案】见试题解答内容
【解答】解：连接OB，

∵AB是⊙O的切线，B为切点，
∴∠OBA＝90°，
∴∠BOA+∠A＝90°，
由题意得：
OB＝OC＝AE＝AF＝2，
∴阴影部分的面积＝△AOB的面积﹣（扇形BOC的面积+扇形EAF的面积）
＝AB•OB﹣
＝×4×2﹣π
＝4﹣π，
故答案为：4﹣π．
一十．正多边形和圆（共1小题）
12．（2021•青岛）如图，正方形ABCD内接于⊙O，PA，PD分别与⊙O相切于点A和点D，PD的延长线与BC的延长线交于点E．已知AB＝2，则图中阴影部分的面积为 　5﹣π　．

【答案】5﹣π．
【解答】解：连接AC，OD，
∵四边形BCD是正方形，
∴∠B＝90°，
∴AC是⊙O的直径，∠AOD＝90°，
∵PA，PD分别与⊙O相切于点A和点D，
∴∠PAO＝∠PDO＝90°，
∴四边形AODP是矩形，
∵OA＝OD，
∴矩形AODP是正方形，
∴∠P＝90°，AP＝AO，AC∥PE，
∴∠E＝∠ACB＝45°，
∴△CDE是等腰直角三角形，
∵AB＝2，
∴AC＝2AO＝2，DE＝CD＝2，
∴AP＝PD＝AO＝，
∴PE＝3，
∴图中阴影部分的面积＝（AC+PE）•AP﹣AO2•π＝（2+3）×﹣（）2•π＝5﹣π，
故答案为：5﹣π．

一十一．翻折变换（折叠问题）（共1小题）
13．（2022•青岛）如图，已知△ABC，AB＝AC，BC＝16，AD⊥BC，∠ABC的平分线交AD于点E，且DE＝4．将∠C沿GM折叠使点C与点E恰好重合．下列结论正确的有：　①④　．（填写序号）
①BD＝8
②点E到AC的距离为3
③EM＝
④EM∥AC

【答案】见试题解答内容
【解答】解：在△ABC中，AB＝AC，BC＝16，AD⊥BC，
∴BD＝DC＝BC＝8，故①正确；
如图，过点E作EF⊥AB于点F，EH⊥AC于点H，

∵AD⊥BC，AB＝AC，
∴AE平分∠BAC，
∴EH＝EF，
∵BE是∠ABD的角平分线，
∵ED⊥BC，EF⊥AB，
∴EF＝ED，
∴EH＝ED＝4，故②错误；
由折叠性质可得：EM＝MC，DM+MC＝DM+EM＝CD＝8，
设DM＝x，则EM＝8﹣x，
Rt△EDM中，EM2＝DM2+DE2，
∴（8﹣x）2＝42+x2，
解得：x＝3，
∴EM＝MC＝5，故③错误；
设AE＝a，则AD＝AE+ED＝4+a，BD＝8，
∴AB2＝（4+a）2+82，
∵＝，
∴，
∴，
∴AB＝2a，
∴（4+a）2+82＝（2a）2，
解得：a＝或a＝﹣4（舍去），
∴tanC＝＝，
又∵tan∠EMD＝，
∴∠C＝∠EMD，
∴EM∥AC，故④正确，
解法二：连接CE，由内心可知CE平分∠ACD，

∴∠GCE＝∠ECD，
由折叠可知CM＝EM，
∴∠MEC＝∠ECM，
∴∠MEC＝∠GCE，
∴EM∥AC，故④正确，
故答案为：①④．
一十二．相似三角形的判定与性质（共1小题）
14．（2021•青岛）已知正方形ABCD的边长为3，E为CD上一点，连接AE并延长，交BC的延长线于点F，过点D作DG⊥AF，交AF于点H，交BF于点G，N为EF的中点，M为BD上一动点，分别连接MC，MN．若，则MN+MC的最小值为 　2　．

【答案】2．
【解答】解：∵四边形ABCD是正方形，
∴A点与C点关于BD对称，
∴CM＝AM，
∴MN+CM＝MN+AM≥AN，
∴当A、M、N三点共线时，MN+CM的值最小，
∵AD∥CF，
∴∠DAE＝∠F，
∵∠DAE+∠DEH＝90°，
∵DG⊥AF，
∴∠CDG+∠DEH＝90°，
∴∠DAE＝∠CDG，
∴∠CDG＝∠F，
∴△DCG∽△FCE，
∵，
∴＝，
∵正方形边长为3，
∴CF＝6，
∵AD∥CF，
∴＝＝，
∴DE＝1，CE＝2，
在Rt△CEF中，EF2＝CE2+CF2，
∴EF＝＝2，
∵N是EF的中点，
∴EN＝，
在Rt△ADE中，EA2＝AD2+DE2，
∴AE＝＝，
∴AN＝2，
∴MN+MC的最小值为2，
故答案为：2．
一十三．用样本估计总体（共1小题）
15．（2021•青岛）在一个不透明的袋中装有若干个红球和4个黑球，每个球除颜色外完全相同，摇匀后从中摸出一个球，记下颜色后再放回袋中，不断重复这一过程，共摸球100次，其中有40次摸到黑球，估计袋中红球的个数是 　6　．
【答案】6．
【解答】解：设袋中红球的个数是x个，根据题意得：
＝，
解得：x＝6，
经检验：x＝6是分式方程的解，
即估计袋中红球的个数是6个，
故答案为6．
一十四．条形统计图（共1小题）
16．（2021•青岛）已知甲、乙两队员射击的成绩如图，设甲、乙两队员射击成绩的方差分别为S甲2、S乙2，则S甲2　＞　S乙2（填“＞”、“＝”、“＜”）．

【答案】＞．
【解答】解：甲射击的成绩为：6，7，7，7，8，8，9，9，9，10，
乙射击的成绩为：6，7，7，8，8，8，8，9，9，10，
则甲＝×（6+7×3+8×2+9×3+10）＝8，
乙＝×（6+7×2+8×4+9×2+10）＝8，
∴S甲2＝×[（6﹣8）2+3×（7﹣8）2+2×（8﹣8）2+3×（9﹣8）2+（10﹣8）2]
＝×[4+3+3+4]
＝1.4；
S乙2＝×[（6﹣8）2+2×（7﹣8）2+4×（8﹣8）2+2×（9﹣8）2+（10﹣8）2]
＝×[4+2+2+4]
＝1.2；
∵1.4＞1.2，
∴S甲2＞S乙2，
故答案为：＞．
一十五．加权平均数（共1小题）
17．（2022•青岛）小明参加“建团百年，我为团旗添光彩”主题演讲比赛，其演讲形象、内容、效果三项分别是9分、8分、8分．若将三项得分依次按3：4：3的比例确定最终成绩，则小明的最终比赛成绩为 　8.3　分．
【答案】8.3．
【解答】解：根据题意得：
＝8.3（分）．
故小明的最终比赛成绩为8.3分．
故答案为：8.3．
一十六．极差（共1小题）
18．（2023•青岛）小颖参加“歌唱祖国”歌咏比赛，六位评委对小颖的打分（单位：分）如下：7，8，7，9，8，10．这六个分数的极差是 　3　分．
【答案】3．
【解答】解：∵这组数据的最大值是10，最小值是7，
∴这六个分数的极差是：10﹣7＝3（分），
故答案为：3．