

山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(提升题)
展开山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(提升题)
一.规律型:点的坐标(共1小题)
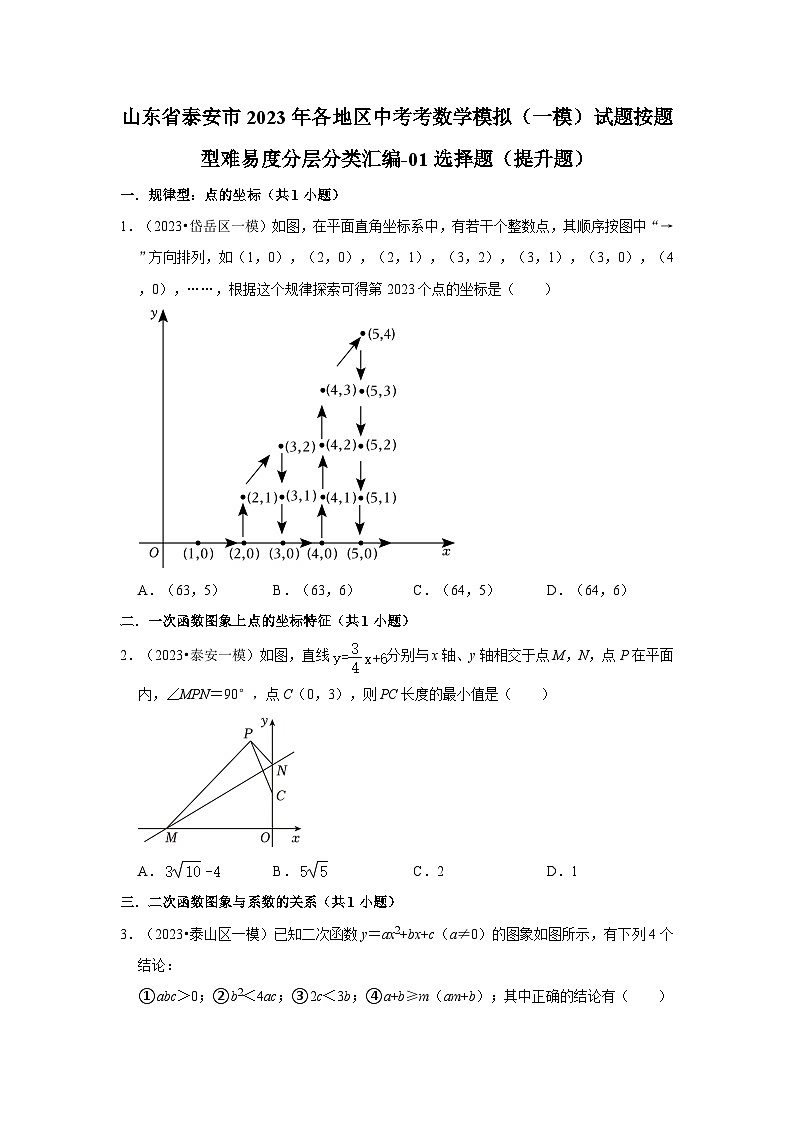
1.(2023•岱岳区一模)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),……,根据这个规律探索可得第2023个点的坐标是( )
A.(63,5) B.(63,6) C.(64,5) D.(64,6)
二.一次函数图象上点的坐标特征(共1小题)
2.(2023•泰安一模)如图,直线分别与x轴、y轴相交于点M,N,点P在平面内,∠MPN=90°,点C(0,3),则PC长度的最小值是( )
A. B. C.2 D.1
三.二次函数图象与系数的关系(共1小题)
3.(2023•泰山区一模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b2<4ac;③2c<3b;④a+b≥m(am+b);其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
四.全等三角形的判定与性质(共1小题)
4.(2023•新泰市一模)如图,在平面直角坐标系中,点O的坐标为(0,0),点M的坐标为(3,0),N为y轴上一动点,连接MN,将线段MN绕点M逆时针旋转60°得到线段MK,连接NK,OK,求线段OK长度的最小值( )
A. B. C.2 D.2
五.等腰三角形的性质(共1小题)
5.(2023•泰安一模)如图,m∥n,△ABC的顶点C在直线m上,若AB=AC,∠A=40°,∠1=20°,则∠2的度数为( )
A.50° B.40° C.45° D.60°
六.平行四边形的判定与性质(共1小题)
6.(2023•泰安一模)如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连接GD、BH,则下列结论:①AG=CH;②DE+CF=4;③S四边形ABFE=3;④四边形BGDH为平行四边形.其中正确的有( )
A.①②③④ B.①③④ C.①②④ D.①②③
七.正方形的性质(共1小题)
7.(2023•岱岳区一模)如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF.其中正确结论的序号为( )
A.①②③④ B.①②④ C.②④ D.①②③
八.四边形综合题(共1小题)
8.(2023•宁阳县一模)如图,Rt△ABE中,∠B=90°,AB=BE,将△ABE绕点A逆时针旋转45°,得到△AHD,过D作DC⊥BE交BE的延长线于点C,连接BH并延长交DC于点F,连接DE交BF于点O.下列结论:
①DE平分∠HDC;②DO=OE;③H是BF的中点;④BC﹣CF=2CE;
⑤CD=HF,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
九.旋转的性质(共2小题)
9.(2023•宁阳县一模)已知如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是边BC的中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转(点E不与A,B重合)时,给出以下5个结论:①AE=PF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP;⑤∠ABP=∠APF.上述结论始终正确的有( )
A.2个 B.3个 C.4个 D.5个
10.(2023•新泰市一模)如图,Rt△ABC中,∠A=30°,∠ABC=90°,将Rt△ABC绕点B逆时针方向旋转得到△A′BC′,此时恰好点C在A′C′上,A′B交AC于点E,则△ABE与△ABC的面积之比为( )
A. B. C. D.
一十.相似三角形的判定(共1小题)
11.(2023•东平县一模)如图,在平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=3,则下列结论:①=;②S△BCE=27;③S△ABE=12;④△AEF∽△ACD.其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②
一十一.解直角三角形的应用-方向角问题(共1小题)
12.(2023•泰安一模)某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲侦测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m,请求出点O到BC的距离( )m.(参考数据sin73.7°≈,cos73.7°≈,tan73.7°≈)
A.140m B.340m C.360m D.480m
一十二.方差(共1小题)
13.(2023•泰山区一模)为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据,如表:
甲
4
8
9
9
10
乙
4
5
6
10
10
关于以上数据,说法正确的是( )
A.甲、乙的中位数相同
B.甲、乙的众数相同
C.甲的平均数小于乙的平均数
D.甲的方差小于乙的方差
山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(提升题)
参考答案与试题解析
一.规律型:点的坐标(共1小题)
1.(2023•岱岳区一模)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),……,根据这个规律探索可得第2023个点的坐标是( )
A.(63,5) B.(63,6) C.(64,5) D.(64,6)
【答案】D
【解答】解:把第一个点(1,0)作为第一列,(2,0)和(2,1)作为第二列,
依此类推,则第一列有1个点,第二列有2个点,⋯,
第n列有n个点,则n列共有个点,并且在奇数列点的顺序是由上到下,偶数列点的顺序由下到上,
∵1+2+3+⋯⋯+63=2016,
∴第2023个点一定在第64列,由下到上是第7个点,
因而第2023个点的坐标是(64,6),
故选:D.
二.一次函数图象上点的坐标特征(共1小题)
2.(2023•泰安一模)如图,直线分别与x轴、y轴相交于点M,N,点P在平面内,∠MPN=90°,点C(0,3),则PC长度的最小值是( )
A. B. C.2 D.1
【答案】D
【解答】解:如图,以MN为直径作⊙E,连接EC并延长交⊙E于点P′,此时P′C的长度最小,
当x=0时,y=0+6=6,
∴点N的坐标为(0,6);
当y=0时,x+6=0,
解得:x=﹣8,
∴点M的坐标为(﹣8,0).
∴MN===10,点E的坐标为(﹣4,3).
又∵点C的坐标为(0,3),
∴CE=4,
∴CP′=EP′﹣CE=MN﹣CE=×10﹣4=1.
故选:D.
三.二次函数图象与系数的关系(共1小题)
3.(2023•泰山区一模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b2<4ac;③2c<3b;④a+b≥m(am+b);其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=1,
∴﹣=1,
∴b=﹣2a>0,
∵抛物线与y轴交点在x轴上方,
∴c>0,
∴abc<0,①错误.
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
∴b2>4ac,②错误.
∵b=﹣2a,
∴a=﹣,
由图象可得x=﹣1时,y<0,
∴a﹣b+c=﹣b+c<0,
∴2c<3b,③正确.
∵x=1时,函数取最大值,
∴a+b+c≥am2+bm+c,
∴a+b≥m(am+b),④正确.
故选:B.
四.全等三角形的判定与性质(共1小题)
4.(2023•新泰市一模)如图,在平面直角坐标系中,点O的坐标为(0,0),点M的坐标为(3,0),N为y轴上一动点,连接MN,将线段MN绕点M逆时针旋转60°得到线段MK,连接NK,OK,求线段OK长度的最小值( )
A. B. C.2 D.2
【答案】A
【解答】解:∵将线段MN绕点M逆时针旋转60°得到线段MK,
∴MN=MK,∠NMK=60°,
∴△MNK是等边三角形,
∴MK=MN=NK,∠NMK=∠NKM=∠KNM=60°,
如图将△MOK绕点M顺时针旋转60°,得到△MQN,连接OQ,
∴△MOK≌△MQN,∠OMQ=60°,
∴OK=NQ,MO=MQ,
∴△MOQ是等边三角形,
∴∠QOM=60°,
∴∠NOQ=30°,
∵OK=NQ,
∴当NQ为最小值时,OK有最小值,
由垂线段最短可得:当QN⊥y轴时,NQ有最小值,
此时,QN⊥y轴,∠NOQ=30°,
∴NQ=OQ=,
∴线段OK长度的最小值为.
故选:A.
五.等腰三角形的性质(共1小题)
5.(2023•泰安一模)如图,m∥n,△ABC的顶点C在直线m上,若AB=AC,∠A=40°,∠1=20°,则∠2的度数为( )
A.50° B.40° C.45° D.60°
【答案】A
【解答】解:作BD∥m,如图,
∴∠DBC=∠1=20°,
∵m∥n,
∴BD∥n,
∵△CAB为等腰三角形,∠A=40°,
∴∠ABC=70°,
∴∠ABD=50°,
∴∠2=∠ABD=50°.
故选:A.
六.平行四边形的判定与性质(共1小题)
6.(2023•泰安一模)如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连接GD、BH,则下列结论:①AG=CH;②DE+CF=4;③S四边形ABFE=3;④四边形BGDH为平行四边形.其中正确的有( )
A.①②③④ B.①③④ C.①②④ D.①②③
【答案】A
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BGO=∠DHO,∠OBG=∠ODH,
∵O是平行四边形ABCD的对角线的交点,
∴OB=OD,
在△BOG和△DOH中,
,
∴△BOG≌△DOH(AAS),
∴BG=DH,
∴AG=CH,所以①正确;
∵BG=DH,BG∥DH,
∴四边形BGDH为平行四边形,所以④正确;
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠∠AEG=∠BFG,
∵∠BFG=∠CFH,
∴∠AEG=∠CFH,
在△AEG和△CFH中,
,
∴△AEG≌△CFH,
∴AE=CF,
∴DE+CF=DE+AE=AD=BC=4,所以②正确;
过点A作AM⊥BC于M,在Rt△ABM中,∠ABC=60°,AB=3,
∴AM=ABsin∠ABC=3×sin60°=,
∴S平行四边形ABCD=BC×AM=4×=6,
∵△BOG≌△DOH,△AEG≌△CFH,
∴S四边形ABOE=S四边形CDOF,
根据题意△BOF≌△DOE,
∴S△BOF=S△DOE,
∴S四边形ABFE=S四边形CDEF=S平行四边形ABCD=×6=3,所以③正确;
即:正确的有①②③④,
故选:A.
七.正方形的性质(共1小题)
7.(2023•岱岳区一模)如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF.其中正确结论的序号为( )
A.①②③④ B.①②④ C.②④ D.①②③
【答案】B
【解答】解:∵PE⊥BC于点E,PF⊥CD于点F,CD⊥BC,
∴PF∥BC,
∴∠DPF=∠DBC,
∵四边形ABCD是正方形,
∴∠DBC=45°,
∴∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC=DF,
在Rt△DPF中,DP2=DF2+PF2=DF2+DF2=2DF2,
∴,
故①正确;
②∵PE⊥BC,PF⊥CD,∠BCD=90°,
∴四边形PECF为矩形,
∴四边形PECF的周长=2CE+2PE=2CE+2BE=2BC=8,
故②正确;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°或90°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,
故③错误;
④连接PC,
∵四边形PECF为矩形,
∴PC=EF,∠PFE=∠ECP,
∵正方形为轴对称图形,
∴AP=PC,
∴AP=EF,
故④正确;
故选:B.
八.四边形综合题(共1小题)
8.(2023•宁阳县一模)如图,Rt△ABE中,∠B=90°,AB=BE,将△ABE绕点A逆时针旋转45°,得到△AHD,过D作DC⊥BE交BE的延长线于点C,连接BH并延长交DC于点F,连接DE交BF于点O.下列结论:
①DE平分∠HDC;②DO=OE;③H是BF的中点;④BC﹣CF=2CE;
⑤CD=HF,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
【答案】B
【解答】解:∵∠ABE=90°,AB=BE,
∴∠AEB=∠BAE=45°,AE=BE,
∵将△ABE绕点A逆时针旋转45°,
∴∠DAE=∠AEB=45°,AD=AE=BE,DH=BE,AH=AB,∠ABE=∠AHD=90°,
∴∠DAB=∠ABE=90°,AH=DH=AB=BE,
又∵DC⊥BE,
∴四边形ABCD是矩形,
∴AB=CD=DH,AD=BC=BE,∠BCD=∠DHE=90°,
∵DH=DC,DE=DE,
∴Rt△DEC≌Rt△DEH(HL),
∴HE=EC,∠AED=∠DEC=67.5°,∠CDE=∠HDE=22.5°,
∴DE平分∠HDC,故①正确;
∵AB=AH,∠BAE=45°,
∴∠ABH=∠AHB=67.5°,
∴∠OHE=∠OEH=67.5°,
∴OH=OE,∠DHO=22.5°=∠HDO,
∴DO=HO,
∴OE=OD,故②正确;
如图,连接CH,
∵∠ABH=67.5°,
∴∠CBH=22.5°,
∴∠BFC=67.5°,
∵HE=EC,∠AEB=45°,
∴∠ECH=∠EHC=22.5°,
∴∠HBC=∠HCE,∠FCH=67.5°,
∴BH=CH,∠FCH=∠BFC,
∴HC=HF,
∴BH=HF,
∴点H是BF的中点,故③正确,
如图,过点H作HN⊥BC于N,
∴HN∥CD,
∴△BHN∽△BFC,
∴=,
∴FC=2HN,
∵AE=BE,AH=BE,
∴HE=(﹣1)BE=CE,
∵HN⊥BC,∠AEB=45°,
∴HN=HE=(﹣1)BE,
∴CF=2HN=(2﹣)BE,
∵BC﹣CF=BE+CE﹣CF=BE+(﹣1)BE﹣(2﹣)BE=2(﹣1)BE,
∴BC﹣CF=2CE,故④正确;
∵∠HFD=180°﹣67.5=112.5°,∠HDF=45°,
∴∠HFD≠∠HDF,
∴HF≠DH,
∴HF≠CD,故⑤不合题意,
故选:B.
九.旋转的性质(共2小题)
9.(2023•宁阳县一模)已知如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是边BC的中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转(点E不与A,B重合)时,给出以下5个结论:①AE=PF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP;⑤∠ABP=∠APF.上述结论始终正确的有( )
A.2个 B.3个 C.4个 D.5个
【答案】A
【解答】解:①∵AB=AC,∠BAC=90°,
∴△ABC是等腰直角三角形,
∵点P为BC的中点,
∴∠BAP=∠C=45°,AP=CP,
∵∠EPF是直角,
∴∠APE+∠APF=∠CPF+∠APF=90°,
∴∠APE=∠CPF,
在△AEP和△CPF中,
,
∴△AEP≌△CPF(ASA),
∴PE=PF,
当点E不是AB的中点时,PE≠AE,
此时AE≠PF,
故①错误;
②∵PE=PF,∠EPF=90°,
∴△PEF为等腰直角三角形,
故②正确;
③∵△AEP≌△CPF,
∴S△APE=S△CPF,
∴S四边形AEPF=S△APC,
∴S四边形AEPF=S△ABC,
故③正确;
④根据等腰直角三角形的性质,EF=PE,
所以,EF随着点E的变化而变化,只有当点E为AB的中点时,EF=PE=AP,
故④错误;
⑤∵∠BAC=90°,AB=AC,
∴∠B=45°,
当PF不是∠APC的平分线时,∠APF≠45°,
此时∠ABP≠∠APF,
故∠⑤错误;
故②③正确,
故选:A.
10.(2023•新泰市一模)如图,Rt△ABC中,∠A=30°,∠ABC=90°,将Rt△ABC绕点B逆时针方向旋转得到△A′BC′,此时恰好点C在A′C′上,A′B交AC于点E,则△ABE与△ABC的面积之比为( )
A. B. C. D.
【答案】D
【解答】解:∵∠A=30°,∠ABC=90°,
∴∠ACB=60°,
∵将Rt△ABC绕点B逆时针方向旋转得到△A'BC',
∴BC=BC',∠ACB=∠A'C'B=60°,
∴△BCC'是等边三角形,
∴∠CBC'=60°,
∴∠ABA'=60°,
∴∠BEA=90°,
设CE=a,
在Rt△CBE中,∠ABE=30°,
∴BC=2CE=2a,
在Rt△ABE中,
∴∠A=30°,
∴AC=2BC=4a,
∴AE=AC﹣BE=3a,
∴,
∴,
∴△ABE与△ABC的面积之比为.
故选:D.
一十.相似三角形的判定(共1小题)
11.(2023•东平县一模)如图,在平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=3,则下列结论:①=;②S△BCE=27;③S△ABE=12;④△AEF∽△ACD.其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②
【答案】D
【解答】解:∵四边形ABCD是平行四边形,
∴AO=CO=AC,AD∥BC,AD=BC,
∴△AFE∽△CBE,
∴=,
∵点E是OA的中点,
∴AE=CE,
∴=,
∴=,
∴AF=BC,
∴AF=AD,
∴=,故①正确;
∵S△AEF=3,
∴=()2=,
∴S△BCE=27;故②正确;
∵==,
∴=,
∴S△ABE=9,故③错误;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故选:D.
一十一.解直角三角形的应用-方向角问题(共1小题)
12.(2023•泰安一模)某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲侦测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m,请求出点O到BC的距离( )m.(参考数据sin73.7°≈,cos73.7°≈,tan73.7°≈)
A.140m B.340m C.360m D.480m
【答案】D
【解答】解:作OM⊥BC于M,ON⊥AC于N,
则四边形ONCM为矩形,
∴ON=MC,OM=NC,
设OM=xm,则NC=xm,AN=(840﹣x)m,
在Rt△ANO中,∠OAN=45°,
∴ON=AN=(840﹣x)m,则MC=ON=(840﹣x)m,
在Rt△BOM中,BM==x,
由题意得,840﹣x+x=500,
解得,x=480,
答:点O到BC的距离为480m.
故选:D.
一十二.方差(共1小题)
13.(2023•泰山区一模)为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据,如表:
甲
4
8
9
9
10
乙
4
5
6
10
10
关于以上数据,说法正确的是( )
A.甲、乙的中位数相同
B.甲、乙的众数相同
C.甲的平均数小于乙的平均数
D.甲的方差小于乙的方差
【答案】D
【解答】解:A、甲的中位数为9,乙的中位数为6,故本选项不符合题意;
B、甲的众数为9,乙的众数为10,故本选项不符合题意;
C、甲的平均数为×(4+8+9+9+10)=8,乙的平均数为×(4+5+6+10+10)=7,故本选项不符合题意;
D、甲的方差为×[(4﹣8)2+(8﹣8)2+(9﹣8)2+(9﹣8)2+(10﹣8)2]=4.4,
乙的方差为×[(4﹣7)2+(5﹣7)2+(6﹣7)2+(10﹣7)2+(10﹣7)2]=6.4,
甲的方差小于乙的方差,故本选项符合题意;
故选:D.
山东省烟台市2023年各地区中考考数学模拟(一模、二模)试题按题型难易度分层分类汇编-01选择题(提升题): 这是一份山东省烟台市2023年各地区中考考数学模拟(一模、二模)试题按题型难易度分层分类汇编-01选择题(提升题),共11页。
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(提升题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(提升题),共28页。
山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(容易题): 这是一份山东省泰安市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(容易题),共15页。












