山东省威海市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）

这是一份山东省威海市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题），共23页。试卷主要包含了【问题再现】，探索发现等内容，欢迎下载使用。
山东省威海市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）
一．二次函数图象与几何变换（共1小题）
1．（2023•环翠区一模）已知抛物线y＝x2+bx+c经过点（1，0）和点（0，3）．
（1）求此抛物线的解析式；
（2）当自变量x满足﹣1≤x≤3时，求函数值y的取值范围；
（3）将此抛物线沿x轴平移m个单位长度后，当自变量x满足1≤x≤5时，y的最小值为5，求m的值．
二．二次函数综合题（共1小题）
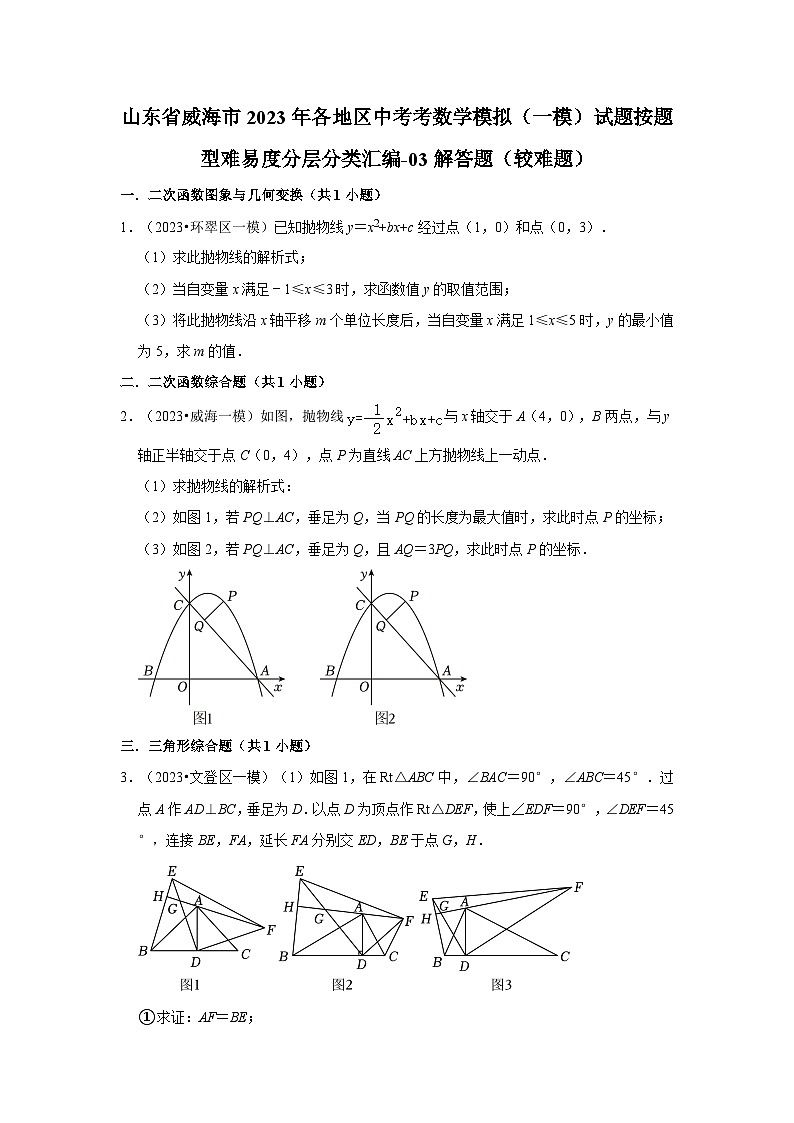
2．（2023•威海一模）如图，抛物线与x轴交于A（4，0），B两点，与y轴正半轴交于点C（0，4），点P为直线AC上方抛物线上一动点．
（1）求抛物线的解析式：
（2）如图1，若PQ⊥AC，垂足为Q，当PQ的长度为最大值时，求此时点P的坐标；
（3）如图2，若PQ⊥AC，垂足为Q，且AQ＝3PQ，求此时点P的坐标．

三．三角形综合题（共1小题）
3．（2023•文登区一模）（1）如图1，在Rt△ABC中，∠BAC＝90°，∠ABC＝45°．过点A作AD⊥BC，垂足为D．以点D为顶点作Rt△DEF，使上∠EDF＝90°，∠DEF＝45°，连接BE，FA，延长FA分别交ED，BE于点G，H．
​
①求证：AF＝BE；
②求证：FH⊥BE．
（2）如图2，在Rt△ABC中，∠BAC＝90°，∠ABC＝30°．过点A作AD⊥BC，垂足为D．以点D为顶点作Rt△DEF，使∠EDF＝90°，∠DEF＝30°，连接BE，FA，延长FA分别交ED，BE于点G，H．
①猜想AF与BE的数量关系并证明；
②猜想FH与BE的位置关系并证明．
中，∠BAC＝90°，∠ABC＝a．过点A作AD⊥BC，垂足为D．
（3）如图3，在​以点D为顶点作Rt△DEF，使∠EDF＝90°，∠DEF＝a．连接BE，FA，延长FA分别交ED，BE于点G，H，则AF与BE的数量关系为 　 　；FH与BE的位置关系为 　 　．
四．四边形综合题（共1小题）
4．（2023•乳山市一模）【问题再现】：
（1）如图1，平行四边形ABCD的对角线交于点O，点E，F在对角线BD上，连接AE，CF．若再增加一个条件，便可证明出AE＝CF．
针对上述问题，小明添加的条件是“DE＝BF”；小强添加的条件是“AE∥CF”．请你替小明或小强完成证明过程；（即任选其中一种方法证明）
【问题探究】：
（2）如图2，平行四边形ABCD的对角线交于点O，过点B的直线与对角线AC交于点P，分别过点A，C作直线BP的垂线，垂足分别为点E，F，连接OE，OF．
①求证：OE＝OF；
②若∠OEF＝30°，探究AE，CF，OE间的等量关系，并证明；
【问题拓广】：
（3）如图3，平行四边形ABCD的对角线交于点O，过点B的直线与对角线CA的延长线交于点P，分别过点A，C作直线BP的垂线，垂足分别为点E，F，连接OE，OF．若∠OEF的度数记为α，请写出AE，CF，OE间的等量关系，并证明．

五．切线的判定与性质（共1小题）
5．（2023•环翠区一模）如图，AB是⊙O的直径，PB⊥AB，过点B作BC⊥OP交⊙O于点C，垂足为D，连接PC并延长与BA的延长线交于点M．
（1）求证：PM是⊙O的切线；
（2）若，求的值．

六．几何变换综合题（共1小题）
6．（2023•环翠区一模）在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点，连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．
（1）猜想观察：如图1，若α＝60°，BD交AC于点M，则的值是 　 　，直线BD与直线CP相交所成的较小角的度数是 　 　．
（2）类比探究：如图2，若α＝90°，BD与AC，PC分别相交于点M，N．求的值及∠CNM的度数．
（3）解决问题：如图3，当α＝90°时，若P，D，C三点在同一直线上，且DA＝DC，BD交AC于点M，DM＝2﹣，求AP的长．

七．相似形综合题（共1小题）
7．（2023•威海一模）（1）探索发现：如图1，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点，F是BC边上一点，∠CDF＝45°，求证：AC•BF＝AD•BD．
（2）尝试应用：如图2，在△ABC中，，∠B＝45°，以A为直角顶点作等腰直角三角形ADE，点D在BC上，点E在AC上，若，求CD的长．
（3）拓展提高：如图3，在等腰△ABC中，AB＝AC＝4，E为AB中点，D为AE中点，过点D作直线DM∥BC交AC于M，在直线DM上取一点F，连接BF交CE于点H；若当∠FHC＝∠ABC时，DF•BC的值为定值，请直接写出该定值为 　 　．


八．列表法与树状图法（共1小题）
8．（2023•环翠区一模）某商场为掌握国庆节期间顾客购买商品时刻的分布情况，统计了10月1日7：00﹣23：00这一时间段内5000名顾客的购买时刻．顾客购买商品时刻的频数分布直方图和扇形统计图如图所示，将7：00﹣23：00这一时间段划分为四个小的时间段：A段为7：00≤t＜11：00，B段为11：00≤t＜15：00，C段为15：00≤t＜19：00，D段为19：00≤t≤23：00，其中t为顾客购买商品的时刻，扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1：3：4：2．

请根据上述信息解答下列问题：
（1）通过计算将频数分布直方图补充完整，并直接写出顾客购买商品时刻的中位数落在哪个时间段？
（2）求10月1日这天顾客购买商品时刻的平均值（同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表，例如，A段的中点值为：＝9）；
（3）为活跃节日气氛，该商场设置购物后抽奖活动，设立了特等奖一个，一等奖两个，二等奖若干，并随机分配到A，B，C，D四个时间段中．
①请直接写出特等奖出现在A时间段的概率；
②请利用画树状图或列表的方法，求两个一等奖出现在不同时间段的概率．

山东省威海市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）
参考答案与试题解析
一．二次函数图象与几何变换（共1小题）
1．（2023•环翠区一模）已知抛物线y＝x2+bx+c经过点（1，0）和点（0，3）．
（1）求此抛物线的解析式；
（2）当自变量x满足﹣1≤x≤3时，求函数值y的取值范围；
（3）将此抛物线沿x轴平移m个单位长度后，当自变量x满足1≤x≤5时，y的最小值为5，求m的值．
【答案】（1）y＝x2﹣4x+3；
（2）﹣1≤y≤8；
（3）m的值为3+或1+．
【解答】解：（1）∵抛物线y＝x2+bx+c经过点（1，0）和点（0，3），
∴，
解得，
∴此抛物线的解析式为y＝x2﹣4x+3；

（2）当x＝﹣1时，y＝1+4+3＝8，
当x＝3时，y＝9﹣12+3＝0，
∵y＝x2﹣4x+3＝（x﹣2）2﹣1，
∴函数图象的顶点坐标为（2，﹣1），
∴当﹣1≤x≤3时，y的取值范围是﹣1≤y≤8；

（3）设此抛物线x轴向右平移m个单位后抛物线解析式为y＝（x﹣2﹣m） 2﹣1，
∵当自变量x满足 1≤x≤5时，y的最小值为 5，
∴2+m＞5，即m＞3，
此时x＝5时，y＝5，即（5﹣2﹣m） 2﹣1＝5，解得m1＝3+，m2＝3﹣ （舍去）；
设此抛物线沿x轴向左平移m个单位后抛物线解析式为y＝（x﹣2+m） 2﹣1，
∵当自变量x满足1≤x≤5时，y的最小值为5，
∴2﹣m＜1，即m＞1，
此时x＝1时，y＝5，即（1﹣2﹣m）2﹣1＝5，解得m1＝﹣1+，m2＝﹣1﹣ （舍去），
综上所述，m的值为3+或1+．
二．二次函数综合题（共1小题）
2．（2023•威海一模）如图，抛物线与x轴交于A（4，0），B两点，与y轴正半轴交于点C（0，4），点P为直线AC上方抛物线上一动点．
（1）求抛物线的解析式：
（2）如图1，若PQ⊥AC，垂足为Q，当PQ的长度为最大值时，求此时点P的坐标；
（3）如图2，若PQ⊥AC，垂足为Q，且AQ＝3PQ，求此时点P的坐标．

【答案】（1）
（2）（2，4）；
（3）（2，4）．
【解答】解：（1）将点A（4，0），C（0，4）代入，
∴，
解得，
∴；
（2）如图1，连接PC，PA，

当PQ的长度最大时，△PAC的面积最大，
作PD∥y轴，交直线AC于点D，
设直线AC的解析式为y＝kx+b′，
代入点A（4，0），C（0，4），
可得：，解得：，
得到直线AC的解析式为y＝﹣x+4，
设点，则D（t，﹣t+4），
∴，
∴，
∴当t＝2时，△PAC面积最大，
∵A（4，0），C（0，4），
∴利用勾股定理可得，
又∵，
∴△PAC面积最大时，PQ也最大，
即t＝2，
此时，点P的坐标为（2，4）；
（3）过点P作PH⊥x轴，垂足为H，交AC于点G，

∵OC＝OA＝4，
∴∠OCA＝∠OAC＝45°，
∵PQ⊥AC，PH⊥x轴，
∴∠HGA＝∠OAC＝45°，
∴∠HGA＝∠PGQ＝45°＝∠QPG，
∴GQ＝PQ，GH＝AH，
∴，，
∵AQ＝3PQ，GQ＝PQ，
∴AG＝2PQ，
∴，即，
∴GH＝PG，
∴G点是PH的中点，
设，G（t，﹣t+4），
∴，
解得t＝2或t＝4（舍），
∴P点坐标为：（2，4）．
三．三角形综合题（共1小题）
3．（2023•文登区一模）（1）如图1，在Rt△ABC中，∠BAC＝90°，∠ABC＝45°．过点A作AD⊥BC，垂足为D．以点D为顶点作Rt△DEF，使上∠EDF＝90°，∠DEF＝45°，连接BE，FA，延长FA分别交ED，BE于点G，H．
​
①求证：AF＝BE；
②求证：FH⊥BE．
（2）如图2，在Rt△ABC中，∠BAC＝90°，∠ABC＝30°．过点A作AD⊥BC，垂足为D．以点D为顶点作Rt△DEF，使∠EDF＝90°，∠DEF＝30°，连接BE，FA，延长FA分别交ED，BE于点G，H．
①猜想AF与BE的数量关系并证明；
②猜想FH与BE的位置关系并证明．
中，∠BAC＝90°，∠ABC＝a．过点A作AD⊥BC，垂足为D．
（3）如图3，在​以点D为顶点作Rt△DEF，使∠EDF＝90°，∠DEF＝a．连接BE，FA，延长FA分别交ED，BE于点G，H，则AF与BE的数量关系为 　AF＝BE•tana　；FH与BE的位置关系为 　FH⊥BE　．
【答案】（1）见详解；（2）见详解；（3）AF＝BE•tana，FH⊥BE．
【解答】（1）证明：①∵∠BAC＝90°，∠ABC＝45°，
∴△ABC是等腰直角三角形，
∵AD⊥BC，
∴∠BDA＝90°，∠BAD＝45°，即BD＝AD，
∵∠EDF＝90°，
∴∠BDA+∠EDA＝∠ADF+∠EDA，即∠BDA＝∠ADF，
∵∠DEF＝45°，
∴∠DFE＝45°，则ED＝DF，
在△BED和△AFD中，
，
∴△BED≌△AFD（SAS），
∴AF＝BE；
②在①中，知道△BED≌△AFD（SAS），则∠BED＝∠AFD，
∵∠HGE＝∠DGF，
∴∠EHF＝180°﹣∠BED﹣∠HGE，∠EDF＝180°﹣∠AFD﹣∠DGF，
即∠EHF＝∠EDF＝90°，
∴FH⊥BE；
（2）解：①，证明如下：
∵AD⊥BC，
∴∠BDA＝∠EDF＝90°，
即∴∠BDA+∠EDA＝∠ADF+∠EDA，即∠BDA＝∠ADF，
在Rt△ABD中，∠ABC＝30°，
∴，
在Rt△EDF中，∠DEF＝30°，
∴，
∴△ADF∽△BDE，
∴，即；
②FH⊥BE，证明如下：
在①中，知道△ADF∽△BDE，
则∠BED＝∠AFD，
∵∠HGE＝∠DGF，
∴∠EHF＝180°﹣∠BED﹣∠HGE，∠EDF＝180°﹣∠AFD﹣∠DGF，
即∠EHF＝∠EDF＝90°，
∴FH⊥BE；
（3）解：AF＝BEtana，证明如下：
∵AD⊥BC，
∴∠BDA＝∠EDF＝90°，
即∠BDA+∠EDA＝∠ADF+∠EDA，即∠BDA＝∠ADF，
在Rt△ABD中，∠ABC＝a，
∴，
在Rt△EDF中，∠DEF＝a，
∴，
∴△ADF∽△BDE，
∴，即AF＝BE•tana，
FH⊥BE，
证明如下：
∵△ADF∽△BDE，
则∠BED＝∠AFD，
∵∠HGE＝∠DGF，
∴∠EHF＝180°﹣∠BED﹣∠HGE，∠EDF＝180°﹣∠AFD﹣∠DGF，
即∠EHF＝∠EDF＝90°，
∴FH⊥BE．
四．四边形综合题（共1小题）
4．（2023•乳山市一模）【问题再现】：
（1）如图1，平行四边形ABCD的对角线交于点O，点E，F在对角线BD上，连接AE，CF．若再增加一个条件，便可证明出AE＝CF．
针对上述问题，小明添加的条件是“DE＝BF”；小强添加的条件是“AE∥CF”．请你替小明或小强完成证明过程；（即任选其中一种方法证明）
【问题探究】：
（2）如图2，平行四边形ABCD的对角线交于点O，过点B的直线与对角线AC交于点P，分别过点A，C作直线BP的垂线，垂足分别为点E，F，连接OE，OF．
①求证：OE＝OF；
②若∠OEF＝30°，探究AE，CF，OE间的等量关系，并证明；
【问题拓广】：
（3）如图3，平行四边形ABCD的对角线交于点O，过点B的直线与对角线CA的延长线交于点P，分别过点A，C作直线BP的垂线，垂足分别为点E，F，连接OE，OF．若∠OEF的度数记为α，请写出AE，CF，OE间的等量关系，并证明．

【答案】（1）证明见解析过程；
（2）①证明见解析过程；
②CF＝OE+AE，证明见解析过程；
（3）CF＝2OE•sinα﹣AE，证明见解析过程．
【解答】（1）解：【小明】∵平行四边形ABCD的对角线交于点O，
∴OD＝OB，OA＝OC，
∵DE＝BF，
∴OD﹣DE＝OB﹣BF，即：OE＝OF，
又∠AOE＝∠COF，
∴△AOE≌△COF（SAS），
∴AE＝CF；
【小强】∵AE∥CF，
∴∠AEO＝∠CFO．
∵平行四边形ABCD的对角线交于点O，
∴OA＝OC，
又∠AOE＝∠COF，
∴△AOE≌△COF（AAS）．
∴AE＝CF．
（2）①证明：如图，延长EO交CF于点M．

∵平行四边形ABCD的对角线交于点O，
∴OA＝OC，
∵AE⊥BP，CF⊥BP，
∴AE∥CM，
∴∠CMO＝∠AEO，
又∠COM＝∠AOE
∴△AOE≌△COM（AAS）．
∴AE＝CM，OE＝OM．
即．
在Rt△MEF中，．
∴OE＝OF．
②解：CF＝OE+AE．
∵∠OEF＝30°，
∴．
∴MF＝OE．
∵CF＝MF+CM，
∴CF＝OE+AE．

（3）解：CF＝2OE•sinα﹣AE．
如图，延长EO交FC的延长线于点M．

同法（2）可得：△AOE≌△COM．
∴．
在Rt△MEF中，．
∴OE＝OF．
在Rt△MEF中，MF＝EM•sin∠MEF．
即MF＝2OE•sinα．
∵CF＝MF﹣CM，
∴CF＝2OE•sinα﹣AE．
五．切线的判定与性质（共1小题）
5．（2023•环翠区一模）如图，AB是⊙O的直径，PB⊥AB，过点B作BC⊥OP交⊙O于点C，垂足为D，连接PC并延长与BA的延长线交于点M．
（1）求证：PM是⊙O的切线；
（2）若，求的值．

【答案】见试题解答内容
【解答】（1）证明：连接OC，
∵OC＝OB，BC⊥OP，
∴∠COP＝∠BOP，
∵OP＝OP，
∴△PBO≌△PCO（SAS），
∴∠OCP＝∠OBP，
∵PB⊥AB，
∴∠ABP＝90°，
∴∠OCP＝90°，
∴PM是⊙O的切线；
（2）解：连接AC，
∵∠OCP＝∠CDO＝90°，
∴∠OCD＝∠CPO，
∴△OCD∽△OPC，
∴＝，
∴OC2＝OD•OP，
∵，
∴设OD＝x，PD＝9x，
∴OP＝10x，
∴OC＝x，
∴BC＝6x，
∴AC＝＝2x，
∵∠ACM+∠ACO＝∠OCD+∠ACO＝90°，
∴∠ACM＝∠OCD，
∴∠ACM＝∠CPO，
∴AC∥OP，
∴△ACM∽△OPM，
∴＝＝，
∴＝．

六．几何变换综合题（共1小题）
6．（2023•环翠区一模）在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点，连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．
（1）猜想观察：如图1，若α＝60°，BD交AC于点M，则的值是 　1　，直线BD与直线CP相交所成的较小角的度数是 　60°　．
（2）类比探究：如图2，若α＝90°，BD与AC，PC分别相交于点M，N．求的值及∠CNM的度数．
（3）解决问题：如图3，当α＝90°时，若P，D，C三点在同一直线上，且DA＝DC，BD交AC于点M，DM＝2﹣，求AP的长．

【答案】（1）1，60°；
（2），45°；
（3）1．
【解答】解：（1）延长BD交PC于Q，

∵α＝60°，
∴AB＝AC，AD＝AP，
∵∠CAB＝60°＝∠PAD，
∴∠CAB+∠DAC＝∠PAD+∠DAC，
即∠DAB＝∠PAC，
∴在△CPA和△BDA中，
，
∴△CPA≌△BDA（SAS），
∴BD＝CP，
即，
在△CMQ和△AMB中，∠PCA＝∠DBA且∠QMC＝∠BMA，
∴∠CQM＝∠CAB＝60°，
故答案为：1，60°；
（2）∵线段AP绕P点逆时针旋转90°得到线段DP，
∴△PAD是等腰直角三角形，
∴∠APD＝90°，∠PAD＝∠PDA＝45°，
∴＝cos∠PAD＝cos45°＝，
∵CA＝CB，∠ACB＝90°，
∴∠CAB＝∠CBA＝45°，
∴＝cos∠CAB＝cos45°＝，
∴，
又∵∠PAD+∠CAD＝∠CAB+∠CAD，
即∠PAC＝∠DAB，
∴△PAC∽△DAB，
∴∠PCA＝∠DBA，，
即＝，
∵∠BMC＝∠CNM+∠PCA＝∠BAC+∠DBA，∠DBA＝∠PCA，
∴∠CNM＝∠BAC＝45°；
（3）设AP＝PD＝x，则AD＝x，
∵DA＝DC，
∴PC＝PD+CD＝（+1）x，
由（2）知，
∴BD＝PC＝（+1）x＝（2+）x，
∵DA＝DC，
∴∠DCA＝∠DAC，
∵∠PCA＝∠DBA，
∴∠DAC＝∠BAD，
又∵∠ADM＝∠BDA，
∴△ADM∽△BDA，
∴＝，
即AD2＝DM•BD，
∴（x）2＝（2﹣）（2+）x，
解得x＝1或x＝0（舍去），
∴AP＝1．
七．相似形综合题（共1小题）
7．（2023•威海一模）（1）探索发现：如图1，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点，F是BC边上一点，∠CDF＝45°，求证：AC•BF＝AD•BD．
（2）尝试应用：如图2，在△ABC中，，∠B＝45°，以A为直角顶点作等腰直角三角形ADE，点D在BC上，点E在AC上，若，求CD的长．
（3）拓展提高：如图3，在等腰△ABC中，AB＝AC＝4，E为AB中点，D为AE中点，过点D作直线DM∥BC交AC于M，在直线DM上取一点F，连接BF交CE于点H；若当∠FHC＝∠ABC时，DF•BC的值为定值，请直接写出该定值为 　12　．


【答案】（1）证明见解析过程；
（2）5；
（3）12．
【解答】（1）证明：∵∠ABC＝90°，AC＝BC，

∴∠A＝∠B＝45°，
∵∠A+∠ACD＝∠CDF+∠BDF，∠A＝∠CDF＝45°，
∴∠ACD＝∠BDF，
∴△ACD∽△BDF，
∴，
∴AC⋅BF＝AD⋅BD；

（2）解：如图，过点E作EF与CD交于点F，使∠EFD＝45°，

∵∠B＝∠ADE＝45°，
∴∠BAD＝∠EDF，
∴△ABD∽△DFE，
∴，
∵，，
∴，
∵∠EFD＝45°，∠ADE＝45°，
∴∠EFC＝∠DEC＝135°，
∴△EFC∽△DEC，
∴
∵，
∴EC2＝FC•CD＝FC×（4+FC），
∴5＝FC×（4+FC），
∴FC＝1，
∴CD＝5；

（3）解：DF•BC＝12，

如图，在DA的延长线上取一点N，使∠DNF＝∠ABC，
由AB＝AC，DM∥BC，
∴∠ADM＝∠AMD＝∠ABC＝∠ACB，∠FMC＝∠DNF，
∴△FDN∽△ABC，
∴，
即NF•BC＝ND•AB，
又由∠ABC＝∠FHC，得∠ABF+∠FBC＝∠FBC+∠ECB，
∴∠ABF＝∠ECB，
∴△NFB∽△BEC，
∴ 即NF•BC＝NB•BE，
∴NB•BE＝ND•AB，
依题意得：AD＝DE＝1，BE＝2，
∴NB•2＝ND•4，
∴NB＝2ND，
∴ND＝BD＝3，
∴NB＝6，
∴NF•BC＝6×2＝12，
即DF•BC＝12．
故答案为：12．
八．列表法与树状图法（共1小题）
8．（2023•环翠区一模）某商场为掌握国庆节期间顾客购买商品时刻的分布情况，统计了10月1日7：00﹣23：00这一时间段内5000名顾客的购买时刻．顾客购买商品时刻的频数分布直方图和扇形统计图如图所示，将7：00﹣23：00这一时间段划分为四个小的时间段：A段为7：00≤t＜11：00，B段为11：00≤t＜15：00，C段为15：00≤t＜19：00，D段为19：00≤t≤23：00，其中t为顾客购买商品的时刻，扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1：3：4：2．

请根据上述信息解答下列问题：
（1）通过计算将频数分布直方图补充完整，并直接写出顾客购买商品时刻的中位数落在哪个时间段？
（2）求10月1日这天顾客购买商品时刻的平均值（同一时间段内顾客购买商品时刻的平均值用该时段的中点值代表，例如，A段的中点值为：＝9）；
（3）为活跃节日气氛，该商场设置购物后抽奖活动，设立了特等奖一个，一等奖两个，二等奖若干，并随机分配到A，B，C，D四个时间段中．
①请直接写出特等奖出现在A时间段的概率；
②请利用画树状图或列表的方法，求两个一等奖出现在不同时间段的概率．
【答案】（1）补全的统计图见解析，中位数落在C段：15：00≤t＜19：00；
（2）10月1日这天顾客购买商品时刻的平均值为15.8；
（3）两个一等奖出现在不同时间段的概率是．
【解答】解：（1）∵扇形统计图中，A，B，C，D四段各部分圆心角的度数比为1：3：4：2，
∴B段的顾客人数为5000×＝1500（人），C段的顾客人数为5000×＝2000（人），
故补全的统计图如下，

∴中位数落在C段：15：00≤t＜19：00；
（2）（500×9+1500×13+2000×17+21×1000）÷5000＝15.8，
所以，10月1日这天顾客购买商品时刻的平均值为15.8；
（3）
①特等奖出现在A时间段的概率为；
②根据题意，树状图如下：

总共有16种等可能的结果，两个一等奖出现在不同时间段的情况有12种，
故两个一等奖出现在不同时间段的概率是＝．