

山东省淄博市2023年各地区中考考数学模拟(二模)试题按题型难易度分层分类汇编-03解答题(提升题)
展开山东省淄博市2023年各地区中考考数学模拟(二模)试题按题型难易度分层分类汇编-03解答题(提升题)
一.分式的化简求值(共2小题)
1.(2023•桓台县二模)(1)计算:;
(2)先化简,再求值:,其中.
2.(2023•淄川区二模)(1)当x=tan45°时,求代数式的值;
(2)解方程组:.
二.解一元二次方程-公式法(共1小题)
3.(2023•博山区二模)请分别用公式法和配方法两种方法解方程:x2+2x﹣1=0.
三.分式方程的应用(共3小题)
4.(2023•临淄区二模)广西“钦蜜九号”黄金百香果以“味甜浓香”深受广大顾客的喜爱,某超市用3600元购进一批黄金百香果,很快就销售一空;超市又用5400元购进了第二批黄金百香果,此时大量水果上市,所购买的重量是第一批的2倍,但是每千克黄金百香果比第一批便宜了5元.
(1)该超市购进第一批和第二批黄金百香果每千克的单价分别是多少元?
(2)如果这两批黄金百香果都以相同的标价出售,要使两批黄金百香果全部售完后的利润率不低于50%(不计其他因素),则超市应该将黄金百香果至少标价每千克多少元出售?
5.(2023•沂源县二模)小明午休时从单位出发,到距离单位2000米的书店去买书,他先步行800米后,换骑公共自行车(自行车投放点固定)到达书店,全程用时15分钟.已知小明骑自行车的平均速度是步行速度的3倍.(转换出行方式时,所需时间忽略不计)
(1)求小明步行的平均速度;
(2)买完书后,小明原路返回,采取先骑公共自行车后步行.此时离上班时间只剩10分钟,为按时上班,他的骑行速度提升到原来的1.5倍.问:小明按原来的步行速度能按时到单位吗?若不行,他的步行速度至少提升到多少(米/分)?
6.(2023•高青县二模)某汽车网站对两款价格相同,续航里程相同的汽车做了一次评测,一款为燃油车,另一款为纯电新能源车.得到相关数据如下:
燃油车
纯电新能源车
油箱容积:48升
电池容量:90千瓦时
油价:8元/升
电价:0.6元/千瓦时
(1)设两款车的续航里程均为a千米,请用含a的代数式表示燃油车和纯电新能源车的每千米行驶费用;
(2)若燃油车每千米行驶费用比纯电新能源车多0.55元.
①请分别求出这两款车的每千米行驶费用;
②若燃油车和纯电新能源车每年的其它费用分别为4800元和8100元.问:每年行驶里程超过多少千米时,新能源车的年费用更低?(年费用=年行驶费用+年其它费用)
四.解一元一次不等式组(共1小题)
7.(2023•临淄区二模)(1);
(2)解不等式组,并将解集在数轴上表示出来.
五.反比例函数系数k的几何意义(共1小题)
8.(2023•桓台县二模)如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点D,函数的图象经过点A(3,4)和点D.
(1)求点D的坐标;
(2)求▱OABC的面积.
六.反比例函数与一次函数的交点问题(共2小题)
9.(2023•临淄区二模)如图,一次函数y=﹣2x+8的图象与反比例函数的图象交于A(m,6),B(3,n)两点.
(1)求反比例函数的表达式;
(2)求△OAB的面积;
(3)根据图象直接写出不等式的解集.
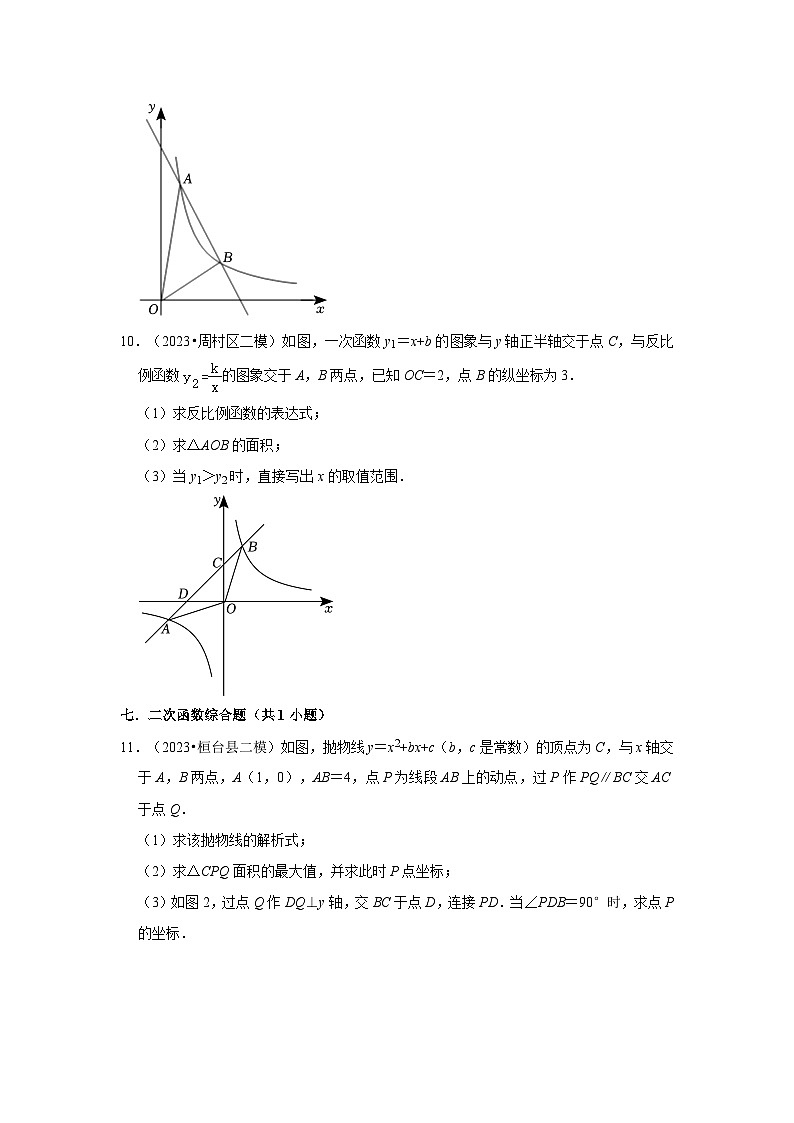
10.(2023•周村区二模)如图,一次函数y1=x+b的图象与y轴正半轴交于点C,与反比例函数的图象交于A,B两点,已知OC=2,点B的纵坐标为3.
(1)求反比例函数的表达式;
(2)求△AOB的面积;
(3)当y1>y2时,直接写出x的取值范围.
七.二次函数综合题(共1小题)
11.(2023•桓台县二模)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC于点Q.
(1)求该抛物线的解析式;
(2)求△CPQ面积的最大值,并求此时P点坐标;
(3)如图2,过点Q作DQ⊥y轴,交BC于点D,连接PD.当∠PDB=90°时,求点P的坐标.
八.全等三角形的判定(共1小题)
12.(2023•高青县二模)如图,在△ABC中,AB=AC,∠B=40°,点D是线段BC上任意一点,连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)若∠BDA=115°,求∠DEC的度数;
(2)若DC=AB,求证:△ABD≌△DCE.
九.全等三角形的判定与性质(共1小题)
13.(2023•周村区二模)如图,已知:AB=DE且AB∥DE,BE=CF.求证:∠A=∠D.
一十.圆周角定理(共1小题)
14.(2023•淄川区二模)如图,AB是⊙O的直径,D,E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE,DE,DF.
(1)求证:∠CFD=∠C;
(2)若∠E=50°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=6,,∠BDE=45°,求EG⋅ED的值.
一十一.切线的性质(共2小题)
15.(2023•桓台县二模)如图,以AB为直径的半圆O中,点D为半圆上不与A,B重合的一个动点,AC平分∠BAD交半圆O于点C,过点C作半圆O的切线EC,交射线AD于点E.
(1)求证:∠E=90°;
(2)若AE=4,AB=6,求AC的长.
16.(2023•周村区二模)如图,AB是⊙O的直径,直线MC与⊙O相切于点C.过点B作BD⊥MC于D,线段BD与⊙O相交于点E.
(1)求证:BC是∠ABD的平分线;
(2)若AB=10,BE=6,求BC的长.
一十二.圆的综合题(共1小题)
17.(2023•临淄区二模)如图,AB为⊙O的直径,弦CD⊥AB于点F,且C为的中点,AE交CD于点G,若AF=2,AE=8,动点M是⊙O上一点,过点D作⊙O的切线,交BA的延长线于点P.
(1)求CF的长;
(2)连接OG,AC,求证:OG⊥AC;
(3)当动点M在⊙O的圆周上运动时,的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.
一十三.作图—基本作图(共1小题)
18.(2023•沂源县二模)如图,已知△ABC,∠BAC=90°.
(1)尺规作图:作△ABC的高AD(保留作图痕迹,不写作法);
(2)若AD=4,tan∠BAD=,求CD的长.
一十四.相似三角形的判定与性质(共1小题)
19.(2023•淄川区二模)如图,在△ABC中,AC=2AB,点E在△ABC的角平分线AD上,且BE=BD.
(1)请利用尺规作图在图中按题意将图形作完整(保留作图痕迹,不写作法):
(2)求证:①△ABE∽△ACD,②E是AD的中点.
山东省淄博市2023年各地区中考考数学模拟(二模)试题按题型难易度分层分类汇编-03解答题(提升题)
参考答案与试题解析
一.分式的化简求值(共2小题)
1.(2023•桓台县二模)(1)计算:;
(2)先化简,再求值:,其中.
【答案】(1)4;
(2);.
【解答】解:(1)
=
=
=4;
(2)
=
=,
当时,
原式=.
2.(2023•淄川区二模)(1)当x=tan45°时,求代数式的值;
(2)解方程组:.
【答案】(1)3;(2).
【解答】解:(1)
=•
=•
=,
当x=tan45°=1时,原式==3;
(2),
将①代入②,得:3(y﹣2)+2y=9,
解得y=3,
将y=3代入①,得x=1,
∴该方程组的解是.
二.解一元二次方程-公式法(共1小题)
3.(2023•博山区二模)请分别用公式法和配方法两种方法解方程:x2+2x﹣1=0.
【答案】,;
【解答】解:配方法,
移项得x2+2x=1,
配方得:x2+2x+1=1+1,即(x+1)2=2,
开方得:,
解得:,;
公式法:
∵a=1,b=2,c=﹣1,
∴b2﹣4ac=22﹣4×1×(﹣1)=8>0,
∴,
∴,.
三.分式方程的应用(共3小题)
4.(2023•临淄区二模)广西“钦蜜九号”黄金百香果以“味甜浓香”深受广大顾客的喜爱,某超市用3600元购进一批黄金百香果,很快就销售一空;超市又用5400元购进了第二批黄金百香果,此时大量水果上市,所购买的重量是第一批的2倍,但是每千克黄金百香果比第一批便宜了5元.
(1)该超市购进第一批和第二批黄金百香果每千克的单价分别是多少元?
(2)如果这两批黄金百香果都以相同的标价出售,要使两批黄金百香果全部售完后的利润率不低于50%(不计其他因素),则超市应该将黄金百香果至少标价每千克多少元出售?
【答案】(1)该超市购进第一批黄金百香果的单价是20元,第二批黄金百香果的单价是15元;
(2)超市应该将每千克黄金百香果至少标价25元出售.
【解答】解:(1)设购进第一批黄金百香果单价为x元,则第二批的单价为(x﹣5)元,
由题意得,,
解得x=20,
检验:当x=20时,x(x﹣5)≠0,
∴x=20是原分式方程的解.
∴x﹣5=20﹣5=15(元),
答:该超市购进第一批黄金百香果的单价是20元,第二批黄金百香果的单价是15元.
(2)由(1)可得,第一批购进(千克),第二批购进180×2=360(千克),
设每千克黄金百香果标价a元,
由题意得,(180+360)a≥(3600+5400)×(1+50%),
解得a≥25,
答:超市应该将每千克黄金百香果至少标价25元出售.
5.(2023•沂源县二模)小明午休时从单位出发,到距离单位2000米的书店去买书,他先步行800米后,换骑公共自行车(自行车投放点固定)到达书店,全程用时15分钟.已知小明骑自行车的平均速度是步行速度的3倍.(转换出行方式时,所需时间忽略不计)
(1)求小明步行的平均速度;
(2)买完书后,小明原路返回,采取先骑公共自行车后步行.此时离上班时间只剩10分钟,为按时上班,他的骑行速度提升到原来的1.5倍.问:小明按原来的步行速度能按时到单位吗?若不行,他的步行速度至少提升到多少(米/分)?
【答案】(1)小明步行的平均速度为80米/分
(2)小明按原来的步行速度不能按时到单位,若想按时到达,他的步行速度至少提升到120米/分.
【解答】解:(1)设小明步行的平均速度为x米/分,则小明骑自行车的平均速度为3x米/分,
依题意得:,
解得:x=80,
经检验,x=80是原方程的解,且符合题意,
∴3x=240.
答:小明步行的平均速度为80米/分.
(2)由(1)得小明原来骑自行车的速度为240米/分,
∵(分钟),,
∴小明按原来的步行速度不能按时到单位.
设他的步行速度应提升到y米/分,
依题意得:,
解得:y≥120,
∴他的步行速度至少提升到120米/分.
答:小明按原来的步行速度不能按时到单位,若想按时到达,他的步行速度至少提升到120米/分.
6.(2023•高青县二模)某汽车网站对两款价格相同,续航里程相同的汽车做了一次评测,一款为燃油车,另一款为纯电新能源车.得到相关数据如下:
燃油车
纯电新能源车
油箱容积:48升
电池容量:90千瓦时
油价:8元/升
电价:0.6元/千瓦时
(1)设两款车的续航里程均为a千米,请用含a的代数式表示燃油车和纯电新能源车的每千米行驶费用;
(2)若燃油车每千米行驶费用比纯电新能源车多0.55元.
①请分别求出这两款车的每千米行驶费用;
②若燃油车和纯电新能源车每年的其它费用分别为4800元和8100元.问:每年行驶里程超过多少千米时,新能源车的年费用更低?(年费用=年行驶费用+年其它费用)
【答案】(1)燃油车每千米行驶费用为元,纯电新能源车每千米行驶费用为元;
(2)①燃油车每千米行驶费用为0.64元,纯电新能源车每千米行驶费用为0.09元;
②当每年行驶里程大于6000千米时,买新能源车的年费用更低.
【解答】解:(1)燃油车每千米行驶费用为=(元),纯电新能源车每千米行驶费用为=(元),
答:燃油车每千米行驶费用为元,纯电新能源车每千米行驶费用为元;
(2)①由题意得:﹣=0.55,
解得:a=600,
经检验,a=600是分式方程的解,且符合题意,
∴=0.64(元),=0.09(元),
答:燃油车每千米行驶费用为0.64元,纯电新能源车每千米行驶费用为0.09元;
②设每年行驶里程为x千米时,买新能源车的年费用更低,
由题意得:0.64x+4800>0.09x+8100,
解得:x>6000,
答:当每年行驶里程大于6000千米时,买新能源车的年费用更低.
四.解一元一次不等式组(共1小题)
7.(2023•临淄区二模)(1);
(2)解不等式组,并将解集在数轴上表示出来.
【答案】(1);
(2)x≥﹣1.
【解答】解:(1)
=
=;
(2),
解①得,x>﹣3;
解②得,x≥﹣1;
∴不等式组的解集是x≥﹣1;
解集在数轴上表示如下:
.
五.反比例函数系数k的几何意义(共1小题)
8.(2023•桓台县二模)如图,平面直角坐标系xOy中,▱OABC的边OC在x轴上,对角线AC,OB交于点D,函数的图象经过点A(3,4)和点D.
(1)求点D的坐标;
(2)求▱OABC的面积.
【答案】(1)D(6,2),(2)36.
【解答】解:(1)∵点A(3,4)在y=上,
∴k=12,
∵四边形OABC是平行四边形,
∴AD=CD,
∴点D的纵坐标为2,
∵点D在y=的图象上,
∴D(6,2).
(2)∵AD=CD,A(3,4),D(6,2)
∴C(9,0);
∴OC=9,
∴平行四边形OABC的周长面积为9×4=36.
六.反比例函数与一次函数的交点问题(共2小题)
9.(2023•临淄区二模)如图,一次函数y=﹣2x+8的图象与反比例函数的图象交于A(m,6),B(3,n)两点.
(1)求反比例函数的表达式;
(2)求△OAB的面积;
(3)根据图象直接写出不等式的解集.
【答案】(1);
(2)8;
(3)0<x<1或x>3.
【解答】解:(1)∵一次函数y=﹣2x+8与反比例函数的图象交于A(m,6),B(3,n)两点.
∴6=﹣2m+8,n=﹣2×3+8,k=6m,
∴m=1,n=2,k=6,
∴点A(1,6),点B(3,2),
反比例函数解析式为:;
(2)∵y=﹣2x+8,
当x=0时,y=8;当y=0时,x=4,
如图所示:C(0,8),D(4,0),
∴OC=8,OD=4,
∴S△OAB=S△COD﹣S△AOC﹣S△BOD===8;
(3)由图象可得当0<x<1或x>3时,反比例函数图象在一次函数的上方.
即不等式的解集为:0<x<1或x>3.
10.(2023•周村区二模)如图,一次函数y1=x+b的图象与y轴正半轴交于点C,与反比例函数的图象交于A,B两点,已知OC=2,点B的纵坐标为3.
(1)求反比例函数的表达式;
(2)求△AOB的面积;
(3)当y1>y2时,直接写出x的取值范围.
【答案】(1)反比例函数的解析式为;
(2)4;
(3)x>1或﹣3<x<0.
【解答】解:(1)∵点C在y轴正半轴,OC=2,
∴b=2,
∴一次函数解析式为y=x+2.
将y=3代入y=x+2,得x=1,
∴B(1,3).
将点B(1,3)代入,得,
∴k=3,
∴反比例函数的解析式为.
(2)将y=0代入y=x+2,得x=﹣2,
∴点D的坐标是(0,﹣2),
∴OD=2.
将y=x+2代入,得,
解得x1=1,x2=﹣3.当x=﹣3时,y=﹣3+2=﹣1,
∴点A的坐标是(﹣3,﹣1),
∵点B的纵坐标为3,
∴.
(3)由图象知:x>1或﹣3<x<0.
七.二次函数综合题(共1小题)
11.(2023•桓台县二模)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC于点Q.
(1)求该抛物线的解析式;
(2)求△CPQ面积的最大值,并求此时P点坐标;
(3)如图2,过点Q作DQ⊥y轴,交BC于点D,连接PD.当∠PDB=90°时,求点P的坐标.
【答案】(1)抛物线的解析式为y=x2+2x﹣3.
(2)△CPQ面积的最大值为2,此时P点坐标为(﹣1,0).
(3)P(﹣,0).
【解答】解:(1)∵抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,
∴B(﹣3,0),
∴将A(1,0),B(﹣3,0)代入y=x2+bx+c得,
,
解得,
∴抛物线的解析式为y=x2+2x﹣3.
答:抛物线的解析式为y=x2+2x﹣3.
(2)过Q作QE⊥x轴于E,过C作CF⊥x轴于F,
设P(m,0),则PA=1﹣m,
∵y=x2+2x﹣3=(x+1)2﹣4,
∴C(﹣1,﹣4),
∴CF=4,
∵PQ∥BC,
∴△PQA∽△BCA,
∴,即,
∴QE=1﹣m,
∴S△CPQ=S△PCA﹣S△PQA
=PA•CF﹣PA•QE
=(1﹣m)×4﹣(1﹣m)(1﹣m)
=﹣(m+1)2+2,
∵﹣3≤m≤1,
∴当m=﹣1时,S△CPQ有最大值为2,
∴△CPQ面积的最大值为2,此时P点坐标为(﹣1,0).
答:△CPQ面积的最大值为2,此时P点坐标为(﹣1,0).
(3)由(1)(2)知,抛物线的解析式为y=x2+2x﹣3,C(﹣1,﹣4),B(﹣3,0),A(1,0),
∴BC:y=﹣2x﹣6,AC:y=2x﹣2,
设P(p,0)(﹣3≤p≤1),
∵PQ∥BC,
∴PQ:y=﹣2x+2p,
∴,解得,
∴Q(,p﹣1),
把y=p﹣1代入y=﹣2x﹣6,得x=﹣,
∴D(﹣,p﹣1),
过点D作DH⊥BP于H,
∴DH=|p﹣1|,PH=,BH=,
∵∠PDB=90°,
∴∠DBP+∠BPD=90°,
∵∠DHB=90°,∠BDH+∠PBD=90°,
∴∠BDH=∠BPD,
∵∠BHD=PHD=90°,
∴△BHD∽△DHP,
∴,
∴DH2=BH•PH,
∴,
∴p=1或p=﹣,
当p=1时,∠PDB不存在,
∴P(﹣,0).
答:P(﹣,0).
八.全等三角形的判定(共1小题)
12.(2023•高青县二模)如图,在△ABC中,AB=AC,∠B=40°,点D是线段BC上任意一点,连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)若∠BDA=115°,求∠DEC的度数;
(2)若DC=AB,求证:△ABD≌△DCE.
【答案】(1)115°;
(2)证明见解析部分.
【解答】(1)解:∵∠B=40°,∠BDA=115°,
∴∠BAD=180°﹣∠B﹣∠BDA=180°﹣40°﹣115°=25°,
∵∠ADE=40°,
∴∠EDC=180°﹣∠BDA﹣∠ADE=180°﹣115°﹣40°=25°,
∵AB=AC,∴∠C=∠B=40°,
∴∠DEC=180°﹣∠EDC﹣∠C=180°﹣25°﹣40°=115°;
(2)证明:∵∠ADC=∠B+∠BAD=40°+∠BAD,∠ADC=∠ADE+∠EDC=40°+∠EDC,
∴∠BAD=∠EDC,
∵AB=AC,
∴∠B=∠C,
∴△ABD≌△DCE(ASA).
九.全等三角形的判定与性质(共1小题)
13.(2023•周村区二模)如图,已知:AB=DE且AB∥DE,BE=CF.求证:∠A=∠D.
【答案】见试题解答内容
【解答】证明:∵AB∥DE,
∴∠B=∠DEF,
∴BE=CF,
∴BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
一十.圆周角定理(共1小题)
14.(2023•淄川区二模)如图,AB是⊙O的直径,D,E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE,DE,DF.
(1)求证:∠CFD=∠C;
(2)若∠E=50°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=6,,∠BDE=45°,求EG⋅ED的值.
【答案】(1)见解析;
(2)100°;
(3).
【解答】(1)证明:如图,连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C,
∵四边形AEDF是⊙O的内接四边形,
∴∠CFD=∠E,
∴∠C=∠CFD;
(2)解:∵∠C=∠CFD=∠E=50°,
∴∠BDF=∠C+∠CFD=100°;
(3)解:如图,连接OE,
∵∠CFD=∠AED=∠C,
∴FD=CD=BD=6,
在Rt△ABD中,,BD=6,
∴AB=9,
∵∠BDE=45°,
∴∠BOE=∠AOE=90°,
∵,
∴,
∵∠AOE=90°,
∴∠ADE=45°,
∵△AEG∽△DEA,
∴,
即.
一十一.切线的性质(共2小题)
15.(2023•桓台县二模)如图,以AB为直径的半圆O中,点D为半圆上不与A,B重合的一个动点,AC平分∠BAD交半圆O于点C,过点C作半圆O的切线EC,交射线AD于点E.
(1)求证:∠E=90°;
(2)若AE=4,AB=6,求AC的长.
【答案】(1)见解析;
(2).
【解答】(1)证明:如图,连接OC.
∵AC平分∠BAD,
∴∠BAC=∠EAC,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠EAC=∠OCA,
∴OC∥AE,
∴∠E+∠OCE=180°,
∵EC是圆O的切线,
∴OC⊥EC,
∴∠OCE=90°,
∴∠E=180°﹣∠OCE=90°;
(2)解:如图,连接BC.
∵AB为半圆O的直径,
∴∠ACB=90°=∠E,
又∵∠BAC=∠EAC,
∴△BAC∽△CAE,
∴,
∵AE=4,AB=6,
∴AC===2.
16.(2023•周村区二模)如图,AB是⊙O的直径,直线MC与⊙O相切于点C.过点B作BD⊥MC于D,线段BD与⊙O相交于点E.
(1)求证:BC是∠ABD的平分线;
(2)若AB=10,BE=6,求BC的长.
【答案】(1)证明见解答;
(2)BC=4.
【解答】(1)证明:连接OC,
∵直线MC与⊙O相切于点C
∴∠OCM=90°,
∵BD⊥CD,
∴∠BDM=90°,
∴∠OCM=∠ADM,
∴OC∥BD,
∴∠DBC=∠BCO,
∵OA=OC,
∴∠BCO=∠CBO,
∴∠DBC=∠CBA,即BC是∠ABD的平分线;
(2)连接AC,连接AE交OC于点F,
∵AB为直径,
∴∠AEB=90°,
∴AE==8,
由(1)知OC∥BD,O为AB的中点,
∴AF=4,
∴OF==3,
∴CF=OC﹣OF=2,
∴AC==2,
∴BC==4.
一十二.圆的综合题(共1小题)
17.(2023•临淄区二模)如图,AB为⊙O的直径,弦CD⊥AB于点F,且C为的中点,AE交CD于点G,若AF=2,AE=8,动点M是⊙O上一点,过点D作⊙O的切线,交BA的延长线于点P.
(1)求CF的长;
(2)连接OG,AC,求证:OG⊥AC;
(3)当动点M在⊙O的圆周上运动时,的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.
【答案】(1)4;
(2)见解答;
(3)的比值不变,比值为.
【解答】(1)解:∵C为的中点,弦CD⊥AB于F,
∴,
∴,
∴AE=DC=8,
∴CF=DF=4,
(2)证明:连接AC,BC,OG,BC交AE于点N,
∵,
∴∠EBC=∠EAC=∠DCA=∠CBA,
∵∠BFE+∠EBC=90°,∠ABC+∠DCB=90°,
∴AG=GC,∠DCB=∠EFB,
∴∠DCB=∠ANC,
∴GN=GC,
∵AO=BO,
∴OG是△OAN的中位线,
∴GO∥BC,
∵AB为⊙O的直径,
∴BC⊥AC,
∴OG⊥AC;
(3)解:的值不变.
理由:如图2,连接DO,则DO⊥PD,DF⊥PO,
∵∠OFD=∠ODP,∠FOD=∠POD,
∴△OFD∽△ODP,
同理△OFD∽△DFP,
则DO2=FO•OP,
DF2=OF•FP,
由(1)知DF=4,
设AO=x,则FO=x﹣2,
故x2=(x﹣2)2+42,
解得:x=5,故FO=3,
即42=3•FP,
∴FP=.
当点M与点A重合时:==,
当点M与点B重合时:=,
当点M不与点A、B重合时:连接FM、PM、MO、DO,
∵DO2=FO•OP,
∴OM2=FO•OP,
∴,
∵∠AOM=∠MOA,
∴△OFM∽△OPM,
∴.
综上所述,的比值不变,比值为.
一十三.作图—基本作图(共1小题)
18.(2023•沂源县二模)如图,已知△ABC,∠BAC=90°.
(1)尺规作图:作△ABC的高AD(保留作图痕迹,不写作法);
(2)若AD=4,tan∠BAD=,求CD的长.
【答案】(1)作图见解析部分.
(2).
【解答】解:(1)如图,线段AD即为所求作.
(2)在Rt△ADB中,tan∠BAD==,
∵AD=4,
∴BD=,
∵∠BAC=∠ADB=∠ADC=90°,
∴∠BAD+∠CAD=90°,∠CAD+∠C=90°,
∴∠BAD=∠C,
∴△ADB∽△CDA,
∴AD2=BD•CD,
∴CD=3.
解法二:此题解法复杂了,∠BAD=∠C,通过tan∠C计算更快.
一十四.相似三角形的判定与性质(共1小题)
19.(2023•淄川区二模)如图,在△ABC中,AC=2AB,点E在△ABC的角平分线AD上,且BE=BD.
(1)请利用尺规作图在图中按题意将图形作完整(保留作图痕迹,不写作法):
(2)求证:①△ABE∽△ACD,②E是AD的中点.
【答案】(1)作法、证明见解答;
(2)①证明见解答;
②证明见解答.
【解答】(1)作法:1.以点A为圆心,适当长为半径作弧交AB于点F,交AC于点G,
2.分别以点F、点G为圆心,大于FG的长为半径弧,两弧在∠BAC内部交于点H,
3.作射线AH交BC于点D,
4.以点B为圆心,BD的长为半径作弧交AD于点E,
5.连接BE,
线段AD和线段BE就是所求的图形.
证明:连接FH、GH,
在△AFH和△AGH中,
,
∴△AFH≌△AGH(SSS),
∴∠FAH=∠GAH,
∴AD是△ABC的角平分线,
由作图得BE=BD,
∴线段AD、线段BE就是所求的图形.
(2)证明:①∵BE=BD,
∴∠BED=∠BDE,
∵AD平分∠BAC,点E在AD上,
∴∠BAE=∠CAD,
∴∠BED﹣∠BAE=∠BDE﹣∠CAD,
∴∠ABE=∠C,
∴△ABE∽△ACD.
②∵△ABE∽△ACD,AC=2AB,
∴==,
∴AE=AD=(AE+DE),
∴AE=DE,
∴E是AD的中点.
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共26页。试卷主要包含了÷÷,其中x为不等式组的整数解,,如图所示,两点,且对称轴为直线x=4等内容,欢迎下载使用。
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(提升题),共26页。试卷主要包含了÷÷,其中x为不等式组的整数解,,如图所示,两点,且对称轴为直线x=4等内容,欢迎下载使用。
山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(基础题): 这是一份山东省淄博市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(基础题),共24页。试卷主要包含了﹣1;,小明解方程﹣=1的过程如下,计算,解不等式组等内容,欢迎下载使用。












