南京12中2022-2023八年级上学期第一次月考数学试卷及答案

这是一份南京12中2022-2023八年级上学期第一次月考数学试卷及答案，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
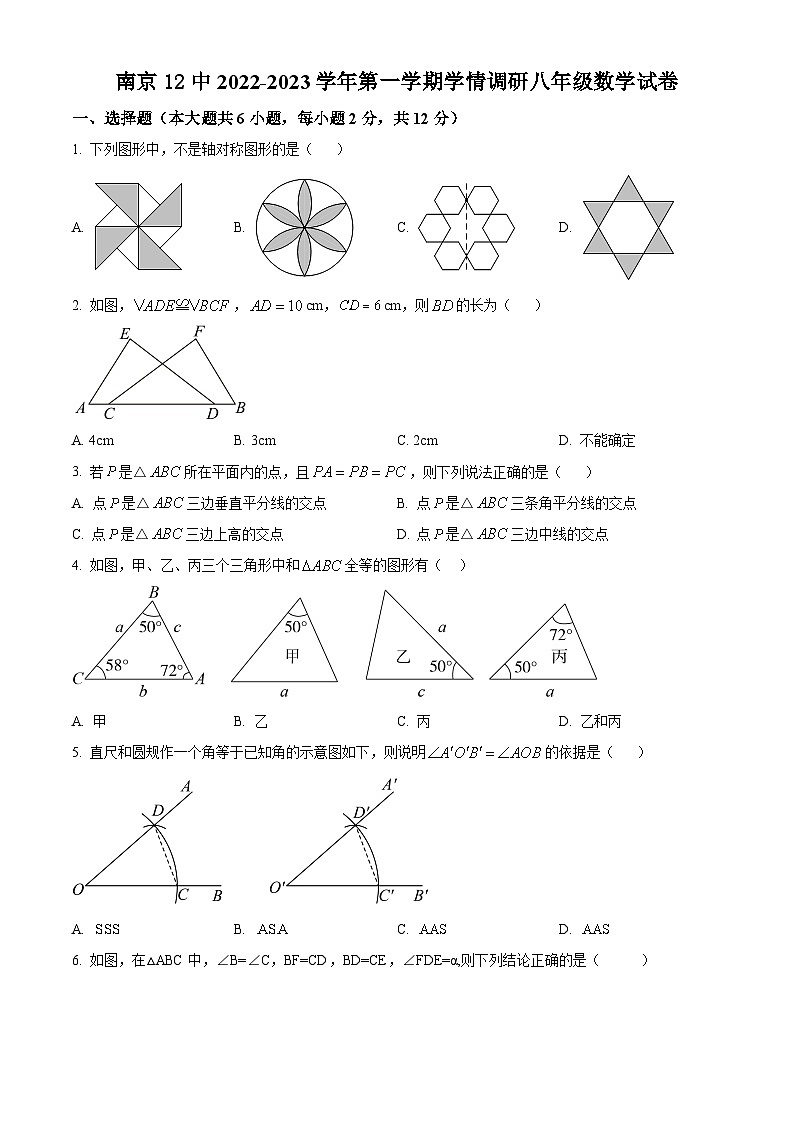
南京12中2022-2023学年第一学期学情调研八年级数学试卷一、选择题（本大题共6小题，每小题2分，共12分）1. 下列图形中，不是轴对称图形的是（    ）A.  B.  C.  D. 2. 如图，，cm，cm，则的长为（    ）A. 4cm B. 3cm C. 2cm D. 不能确定3. 若是△所在平面内的点，且，则下列说法正确的是（    ）A. 点是△三边垂直平分线的交点 B. 点是△三条角平分线的交点C. 点是△三边上高的交点 D. 点是△三边中线的交点4. 如图，甲、乙、丙三个三角形中和全等的图形有（   ）A. 甲 B. 乙 C. 丙 D. 乙和丙5. 直尺和圆规作一个角等于已知角的示意图如下，则说明的依据是（    ）  A.  B.  C.  D. 6. 如图，在△ABC中，∠B=∠C，BF=CD，BD=CE，∠FDE=α,则下列结论正确的是（       ）A. 2α+∠A=180° B. α+∠A=90° C. 2α+∠A=90° D. α+∠A=180°二、填空题（本大题共10小题，每小题2分，共20分）7. 角是轴对称图形，__是它的对称轴．8. 如图，△ABC≌△DEF，请根据图中提供信息，写出x=___．9. 如图，若，，，，，那么_______．10. 如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“HL”判定，还需要加条件_____．
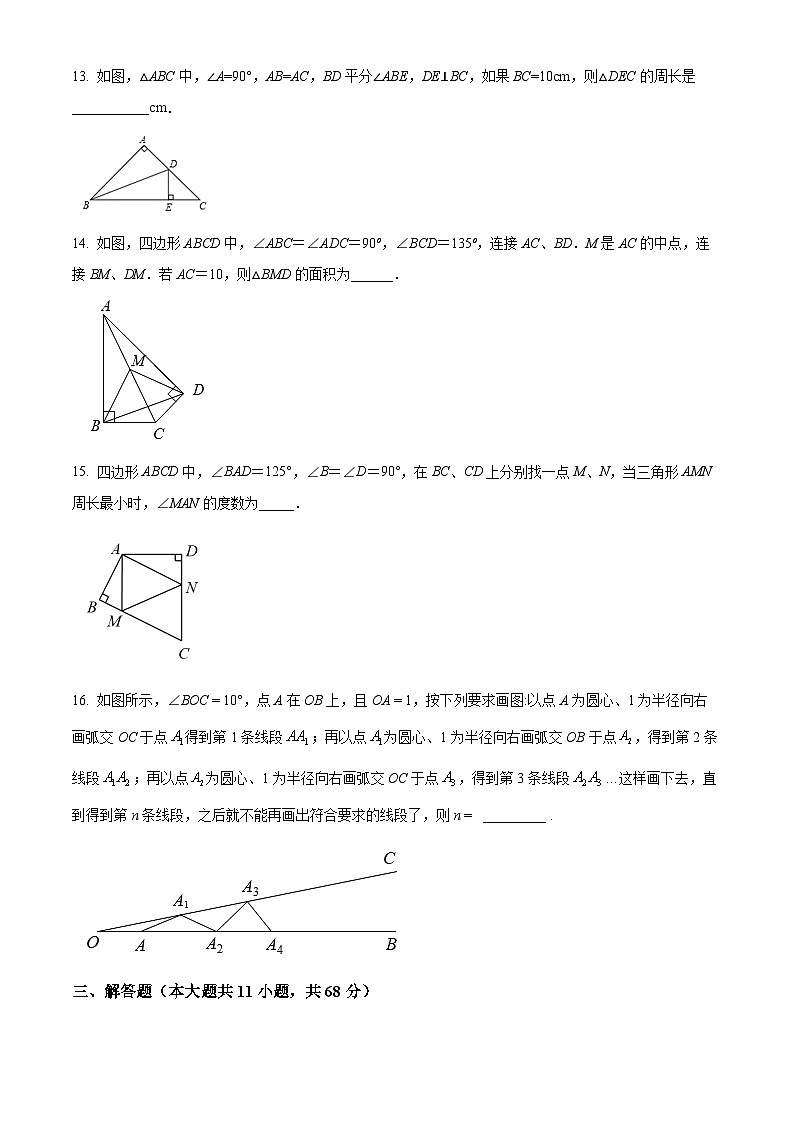
 11. 已知一个等腰三角形，其中一条腰上高与另一条腰的夹角为25°，则该等腰三角形的顶角为________．12. 如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝_____．13. 如图，△ABC中，∠A=90°，AB=AC，BD平分∠ABE，DE⊥BC，如果BC=10cm，则△DEC的周长是___________cm．14. 如图，四边形ABCD中，∠ABC＝∠ADC＝90º，∠BCD＝135º，连接AC、BD．M是AC的中点，连接BM、DM．若AC＝10，则△BMD的面积为______．15. 四边形ABCD中，∠BAD＝125°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，当三角形AMN周长最小时，∠MAN的度数为_____．16. 如图所示，∠BOC = 10°，点A在OB上，且OA = 1，按下列要求画图:以点A为圆心、1为半径向右画弧交OC于点得到第1条线段；再以点为圆心、1为半径向右画弧交OB于点，得到第2条线段；再以点为圆心、1为半径向右画弧交OC于点，得到第3条线段…这样画下去，直到得到第n条线段，之后就不能再画出符合要求的线段了，则n =  _________ .三、解答题（本大题共11小题，共68分）17. 利用网格线用三角尺画图．（1）图中找一点O，使得；（2）在上找一点P，使得P到的距离相等；（3）在射线上找一点Q，使得．    18. 如图，已知线段AB和射线AC，用不带刻度的直尺和圆规完成下列作图．（不写作法，保留作图痕迹）（1）图①中，在射线AC上求作一点D，使得DA＝DB；（2）在图②中，在射线AC上求作一点E，使得∠BAC＝2∠EBA．     19 如图，AB＝DE，AC＝DF，BE＝CF．求证：（1）△ABC≌△DEF；（2）．    20. 如图，AD平分∠BAC，∠BAC+∠ACD=180°，E在AD上，BE的延长线交CD于F，连CE，且∠1=∠2，试说明AB=AC．   21. 如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高．（1）试说明AD垂直平分EF；（2）若AB＝6，AC＝4，S△ABC＝15，求DE的长．   22. 如图，△ABC中，D是BC延长线上一点，满足CD＝AB，过点C作CE∥AB且CE＝BC，连接DE并延长，分别交AC、AB于点F、G．（1）求证：△ABC≌△DCE；（2）若∠B＝50°，∠D＝22°，求∠AFG的度数．   23. 如图，C为线段AB上任意一点（不与A、B重合），在AB的同侧分别作△ACD和△BCE，CA＝CD，CB＝CE，∠ACD与∠BCE都是锐角，且∠ACD＝∠BCE，连接AE交CD于点M，连接BD交CE于点N，AE与BD交于点P，连接PC．试说明：（1）△ACE≌△DCB．（2）PC平分∠APB．         24. 如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．  25. 如图，在中， ，高AD、BE相交于点O，，且．（1）求线段AO的长；（2）动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动，P、Q两点同时出发，当点P到达A点时，P、Q两点同时停止运动．设点P的运动时间为t秒，△POQ的面积为S，请用含t的式子表示S，并直接写出相应的t的取值范围；（3）在（2）的条件下，点F是直线AC上的一点且CF＝BO．是否存在t值，使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等？若存在，请直接写出符合条件的t值；若不存在，请说明理由．
答案1. A2. A3. A4.D5. A6. A7.角平分线所在的直线8. 209. 20度10. AB＝AC11. 65°或115°12. 55°13. 1014.15. 70°16. 817.（1） （2）（3）18.（1）（2）19. （1）证明：∵BE＝CF，BE+CE＝CF+EC∴BC＝EF在△ABC和△DEF中∴△ABC≌△DEF（SSS）（2）证明：∵△ABC≌△DEF∴∠B＝∠DEF∴20.∵∠BAC+∠ACD=180°∴AB∥CD∴∠1=∠又∵∠1=∠2∴∠B=∠2又∵AD平分∠BAC∴∠CAE=∠BAE∵AE=AE∴△ABE≌△ACE∴AB=AC21.（1）∵平分在和中 ∴≌又∴≌是线段的垂直平分线（2）22.（1）证明：∵CE∥AB∴∠B＝∠DCE在△ABC与△DCE中∴△ABC≌△DCE（SAS）（2）解：∵△ABC≌△DCE，∠B＝50°，∠D＝22°∴∠ECD＝∠B＝50°，∠A＝∠D＝22°∵CE∥AB∴∠ACE＝∠A＝22°∵∠CED＝180°﹣∠D﹣∠ECD＝180°﹣22°﹣50°＝108°∴∠AFG＝∠DFC＝∠CED﹣∠ACE＝108°﹣22°＝86°23. （1）∵∠ACD＝∠BCE∴∠ACD+∠DCE＝∠DCE+∠BCE∴∠ACE＝∠DCB在△ACE和△DCB中∴△ACE≌△DCB（SAS）（2）如图，过点C作CH⊥AE于H，CG⊥BD于G由（1）可知，△ACE≌△DCB∴AE＝BD，∴AE和BD边上的高相等，即CH＝CG∴∠APC＝∠BPC∴PC平分∠APB24.证明：如图，在上截取 平分 平分 25.（1） 、是的高，在和中 （2），，设，①如图1，当点在线段上时，的取值范围是②如图2，当点射线上时，的取值范围是（3）存在①如图3中，当时， 解得：②如图4中，当时，解得：综上所述，或时，