

新高考数学一轮复习讲练测专题8.2空间几何体的表面积和体积(练)(含解析)
展开专题8.2 空间几何体的表面积和体积
1.(2021·湖南高一期末)已知圆柱及其展开图如图所示,则其体积为( )
A. B. C. D.
【答案】D
【解析】
结合展开图求出圆柱的底面半径与高,进而结合体积公式即可求出结果.
【详解】
设底面半径为,高为,根据展开图得,则,所以圆柱的体积为,
故选:D.
2.(2021·宁夏大学附属中学高一月考)已知圆柱的上、下底面的中心分别为,过直线的平面截该圆柱所得的面是面积为8的正方形,则该圆柱的表面积为( )
A. B. C. D.
【答案】B
【解析】
根据圆柱的轴截面面积求出圆柱的底面半径和母线长,利用圆柱的表面积公式,即可求解.
【详解】
设圆柱的轴截面的边长为,
因为过直线的平面截该圆柱所得的面是面积为8的正方形,所以,解得,
即圆柱的底面半径为,母线长,
所以圆柱的表面积为.
故选:B.
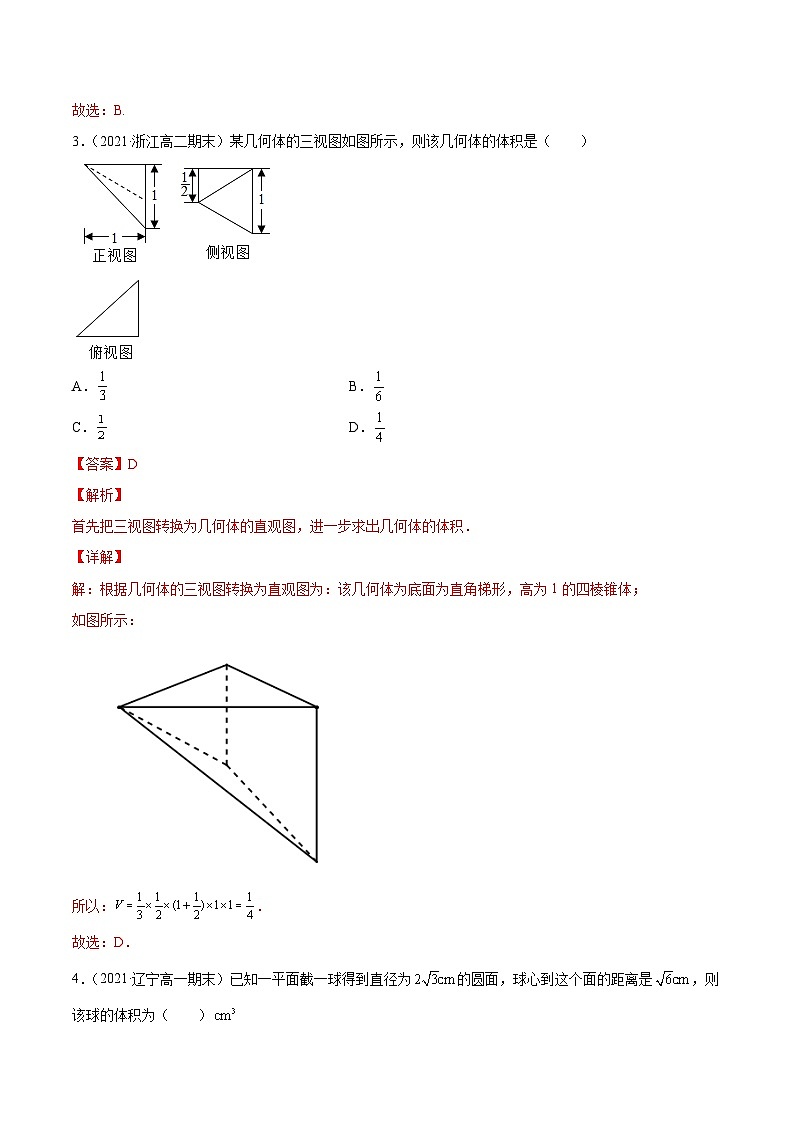
3.(2021·浙江高二期末)某几何体的三视图如图所示,则该几何体的体积是( )
A. B.
C. D.
【答案】D
【解析】
首先把三视图转换为几何体的直观图,进一步求出几何体的体积.
【详解】
解:根据几何体的三视图转换为直观图为:该几何体为底面为直角梯形,高为1的四棱锥体;
如图所示:
所以:.
故选:D.
4.(2021·辽宁高一期末)已知一平面截一球得到直径为的圆面,球心到这个面的距离是,则该球的体积为( )
A. B. C. D.
【答案】B
【解析】
由球的截面性质求得球半径后可得体积.
【详解】
由题意截面圆半径为,所以球半径为,
体积为.
故选:B.
5.(2020·浙江省高考真题)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A. B. C.3 D.6
【答案】A
【解析】
由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,
且三棱锥的一个侧面垂直于底面,且棱锥的高为1,
棱柱的底面为等腰直角三角形,棱柱的高为2,
所以几何体的体积为:
.
故选:A
6.(2018·全国高考真题(文))已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A. B. C. D.
【答案】B
【解析】
根据题意,可得截面是边长为的正方形,
结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,
所以其表面积为,故选B.
7.(2020·江苏省高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半轻为0.5 cm,则此六角螺帽毛坯的体积是____cm.
【答案】
【解析】
正六棱柱体积为
圆柱体积为
所求几何体体积为
故答案为:
9.(2019·北京高考真题(文))某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.
【答案】40.
【解析】
如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱之后余下的几何体,
几何体的体积.
10.(2019·全国高考真题(理))中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.
【答案】共26个面. 棱长为.
【解析】
由图可知第一层与第三层各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有个面.
如图,设该半正多面体的棱长为,则,延长与交于点,延长交正方体棱于,由半正多面体对称性可知,为等腰直角三角形,
,
,即该半正多面体棱长为.
1.(2021·浙江高一期末)我国古代数学名著《九章算术》中记载“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺.问积几何?”这里的“羡除”,是指由三个等腰梯形和两个全等的三角形围成的五面体.在图1所示羡除中,,,,,等腰梯形和等腰梯形的高分别为和,且这两个等腰梯形所在的平面互相垂直.按如图2的分割方式进行体积计算,得该“羡除”的体积为( )
A. B. C. D.
【答案】A
【解析】
由图可知,中间部分为棱柱,两侧为两个全等的四棱锥,再由柱体和锥体的体积公式可求得结果.
【详解】
按照图中的分割方式,中间为直三棱柱,直三棱柱的底面为直角三角形,
两条直角边长分别为、,直三棱柱的高为,
所以,直三棱柱的体积为.
两侧为两个全等的四棱锥,四棱锥的底面为直角梯形,
直角梯形的面积为,四棱锥的高为,
所以,两个四棱锥的体积之和为,
因此,该“羡除”的体积为.
故选:A.
2.(2021·河北巨鹿中学高一月考)蹴鞠(如图所示),又名蹴球、蹴圆、筑球、踢圆等,蹴有用脚蹴、踢的含义,鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴、塌、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗传名录.已知某蹴鞠(近似看作球体)的表面上有四个点、、、,满足为正三棱锥,是的中点,且,侧棱,则该蹴鞠的表面积为( )
A. B. C. D.
【答案】A
【解析】
若,为中点易得,再应用余弦定理、勾股定理求得,即为直三棱锥,即可求外接球半径,进而求表面积.
【详解】
如下图,若为中点,则,又,
∴,又为正三棱锥且侧棱,
∴,若,则,,
在中,,即,可得,,
∴,即为直三棱锥,易得外接球半径,
∴该蹴鞠的表面积为.
故选:A
3.【多选题】(2021·江苏高一期末)已知圆台上、下底面的圆心分别为,,半径为,,圆台的母线与下地面所成角的正切值为,为上一点,则( )
A.圆台的母线长为
B.当圆锥的圆锥的体积相等时,
C.圆台的体积为
D.当圆台上、下底面的圆周都在同一球面上,该球的表面积为
【答案】BCD
【解析】
转化求解圆台的母线长判断Q;利用比例关系判断B;求解体积判断C;取得球的表面积判断D.
【详解】
解:圆台上、下底面的圆心分别为,,半径为2,4,圆台的母线与下底面所成角的正切值为3,为上一点,
,
母线,与圆台的母线长为6矛盾,所以A错误;
,,B正确;
,C正确;
设球心到上底面的距离为,则,解得,,,D正确;
故选:BCD.
4.(2020·全国高考真题(文))已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.
【答案】
【解析】
易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,
其中,且点M为BC边上的中点,
设内切圆的圆心为,
由于,故,
设内切圆半径为,则:
,
解得:,其体积:.
故答案为:.
5.(2020届浙江省杭州市高三3月模拟)在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称为“阳马”.现有一“阳马”,底面,,,则该“阳马”的最长棱长等于______;外接球表面积等于______.
【答案】3
【解析】
如图,底面,底面为长方形,且,,
所以.
最长棱为:3.
该几何体可以通过补体得长方体,所以其外接球的半径为.
则其外接球的表面积为,故答案为:3;.
6.(2020·山东省仿真联考3)在三棱锥中,平面,,,,是上的一动点,且直线与平面所成角的最大值为,则________,三棱锥的外接球的表面积为________.
【答案】6
【解析】
设直线与平面所成的角为,三棱锥外接球的球心为,半径为,
如图所示,则,
所以,则的最小值为,的最小值是,即点到的距离为,所以.
因为,
所以,
所以,
所以,
所以.
取的外接圆的圆心为,则圆的半径.
连接,作于点,
则点为的中点,所以,
故三棱锥的外接球的表面积.
故答案为:6;.
7.(广东省汕尾市2020-2021学年高一下学期期末数学试题)已知某圆柱的轴截面是一个正方形,且该圆柱表面积(底面和侧面面积之和)为,其外接球的表面积为,则该圆柱的表面积与其外接球的表面积的比值________.
【答案】
【解析】
设圆柱的底面半径为,高为,则,上下底面圆圆心连线的中点即为该圆柱外接球的球心,可得外接球的半径,再由圆柱的表面积公式和球的表面积公式分别计算、即可得比值.
【详解】
设圆柱的底面半径为,高为,
因为圆柱的轴截面是一个正方形,
所以,
所以圆柱表面积,
其外接球的球心在上下底面圆圆心连线的中点位置,
可知球心到上底面圆的距离为,
由勾股定理可得:外接球的半径,
所以外接球的表面积,
所以该圆柱的表面积与其外接球的表面积的比值,
故答案为:.
8.(2021·重庆市杨家坪中学高一月考)学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为在一正三棱柱中挖去一个圆柱后的剩余部分(圆柱的上下两底面圆与三棱柱的底面各边相切),圆柱底面直径为,高为.打印所用原料密度为,不考虑打印损耗,制作该模型所需原料的质量为______.(取,,精确到0.1).
【答案】
【解析】
由正三棱柱的性质,结合已知求其底面面积,再由棱柱的体积公式求其体积,并求圆柱的体积为,则模型体积为,即可求制作该模型所需原料的质量.
【详解】
由题意,正三棱柱底面(等边三角形)如上图有且,,,
∴,则,故底面面积,
∴正三棱柱的体积.
而圆柱的体积为,
∴制作该模型所需原料的质量为克.
故答案为:
9.(2021·上海高二期末)五月五是端午,门插艾,香满堂,吃粽子,蘸白糖,粽子古称“角黍”,是我国南北各地的节令食品,因各地风俗不同,粽子的形状和食材也会不同,有一种各面都是正三角形的正四面体形粽子,若该正四面体粽子的棱长为8cm,则现有1立方米体积的食材,最多可以包成这种粽子_______个.
【答案】16572
【解析】
根据题意,利用棱锥的体积公式求得正四面体粽子的体积,进而求得答案.
【详解】
如图所示,正四面体的棱长为,设底面正三角形的中心为,
连接,则平面,
连接,则,所以,
所以一个粽子的体积为:,
由 ,又由
所以1立方米体积的食材,最多可以包成这种粽子个.
故答案为:.
10.(2021·浙江高二期末)在四面体中,,,,,若四面体的外接球半径为,则四面体的体积的最大值为___________.
【答案】
【解析】
根据题意可以将此四面体放入一个长方体中,则易求四面体高与底面长的关系,再根据体积公式写出其体积表达式,最后利用基本不等式即可.
【详解】
如图所示,不妨将四面体放入下图中的长方体中,则长方体的宽为,设长方体的长为,高为.
因为四面体的外接球半径为,
所以此长方体外接球半径为,
则,解得,
所以四面体的体积,当且仅当时等号成立,所以四面体的体积最大值为.
故答案为:
1.(2021·全国高考真题)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
【答案】D
【解析】
由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】
作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高,
下底面面积,上底面面积,
所以该棱台的体积.
故选:D.
2.(2020·天津高考真题)若棱长为的正方体的顶点都在同一球面上,则该球的表面积为( )
A. B. C. D.
【答案】C
【解析】
【分析】
求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.
【详解】
这个球是正方体的外接球,其半径等于正方体的体对角线的一半,
即,
所以,这个球的表面积为.
故选:C.
3.(2021·全国高考真题(理))已如A,B,C是半径为1的球O的球面上的三个点,且,则三棱锥的体积为( )
A. B. C. D.
【答案】A
【解析】
由题可得为等腰直角三角形,得出外接圆的半径,则可求得到平面的距离,进而求得体积.
【详解】
,为等腰直角三角形,,
则外接圆的半径为,又球的半径为1,
设到平面的距离为,
则,
所以.
故选:A.
4.(2020·全国高考真题(理))埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
【答案】C
【解析】
如图,设,则,
由题意,即,化简得,
解得(负值舍去).
故选:C.
5.(2018·全国高考真题(文))设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为( )
A. B. C. D.
【答案】B
【解析】
如图所示,
点M为三角形ABC的中心,E为AC中点,
当平面时,三棱锥体积最大
此时,
,
点M为三角形ABC的中心
中,有
故选B.
6.(2019·全国高考真题(理))已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )
A. B. C. D.
【答案】D
【解析】
解法一:为边长为2的等边三角形,为正三棱锥,
,又,分别为、中点,
,,又,平面,平面,,为正方体一部分,,即 ,故选D.
解法二:
设,分别为中点,
,且,为边长为2的等边三角形,
又
中余弦定理,作于,,
为中点,,,
,,又,两两垂直,,,,故选D.
新高考数学一轮复习讲练测专题7.4数列求和(练)(含解析): 这是一份新高考数学一轮复习讲练测专题7.4数列求和(练)(含解析),共26页。
新高考数学一轮复习讲练测专题8.2空间几何体的表面积和体积(讲)(含解析): 这是一份新高考数学一轮复习讲练测专题8.2空间几何体的表面积和体积(讲)(含解析),共21页。
新高考数学一轮复习讲练测专题3.7函数的图象(练)(含解析): 这是一份新高考数学一轮复习讲练测专题3.7函数的图象(练)(含解析),共26页。












