初中北师大版1 等腰三角形优质ppt课件

这是一份初中北师大版1 等腰三角形优质ppt课件，共27页。PPT课件主要包含了边边边SSS，边角边SAS，角角边ASA，170°，236°，证法一，证法二，证法三等内容，欢迎下载使用。

我们已经学了哪些判定三角形全等的方法？
三边对应相等的两个三角形全等.
两边及其夹角对应相等的两个三角形全等.
两角及其夹边对应相等的两个三角形全等.
我们已经探索过“两角分别相等且其中一组等角的对边相等的两个三角形全等”这个结论，你能用有关的基本事实和已经学习过的定理证明它吗？
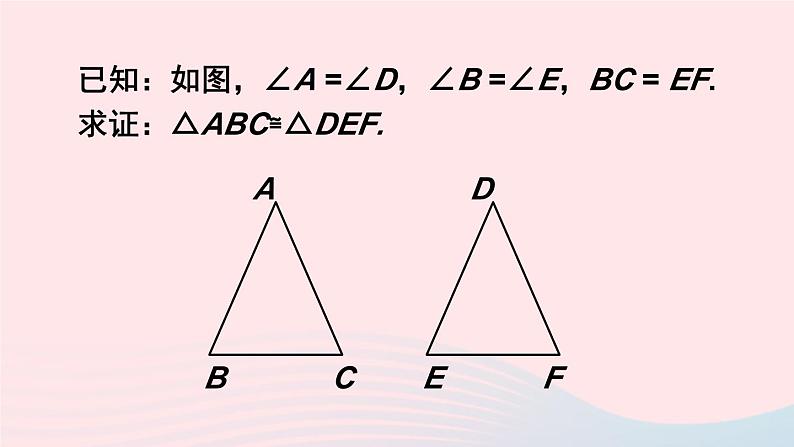
已知：如图，∠A =∠D，∠B =∠E，BC = EF.求证：△ABC≌△DEF.
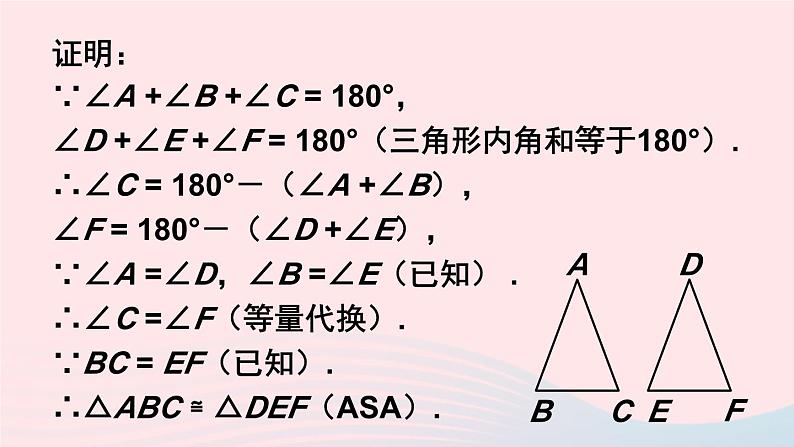
证明：∵∠A +∠B +∠C = 180°，∠D +∠E +∠F = 180°（三角形内角和等于180°）.∴∠C = 180°－（∠A +∠B），∠F = 180°－（∠D +∠E），∵∠A =∠D，∠B =∠E（已知） .∴∠C =∠F（等量代换）.∵BC = EF（已知）.∴△ABC ≌ △DEF（ASA）.
根据全等三角形的定义，我们可以得到
（1）还记得我们探索过的等腰三角形的性质吗？ （2）请你选择等腰三角形的一条性质进行证明，并与同伴交流.
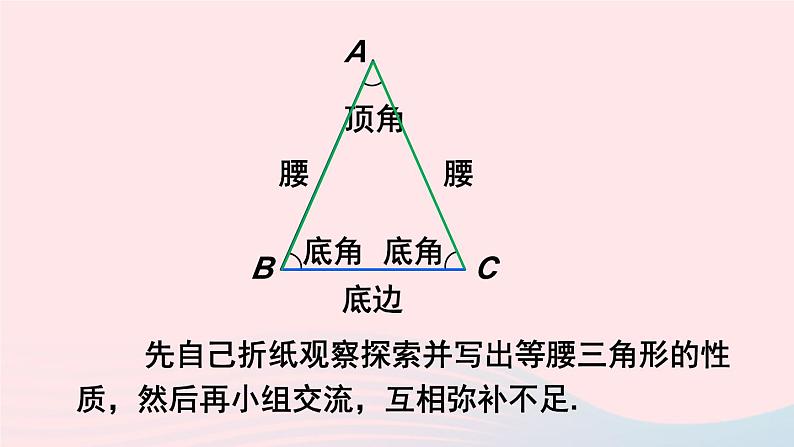
先自己折纸观察探索并写出等腰三角形的性质，然后再小组交流，互相弥补不足.
这一定理可以简述为：等边对等角.
在△ABC 中，AB = AC.（1）若∠A = 40°，则∠C 等于多少度？（2）若∠B = 72°，则∠A 等于多少度？
已知：如图，在△ABC 中，AB = AC.求证：∠B =∠C.
取 BC 的中点 D，连接 AD.在△ABD 和△ACD 中，∵ AB = AC，BD = CD，AD = AD， ∴ △ABD ≌ △ACD（SSS）.∴ ∠B =∠C （全等三角形的对应角相等）.
作△ABC 顶角∠A 的角平分线 AD.在△ABD 和△ACD 中，∵ AB = AC，∠BAD =∠CAD，AD = AD ，∴ △ABD ≌ △ACD（SAS）.∴ ∠B =∠C （全等三角形的对应角相等）.
在△ABC 和△ACB 中，∵ AB = AC，∠A = ∠A，AC = AB， ∴ △ABC ≌△ACB（SAS）.∴ ∠B =∠C （全等三角形的对应角相等）.
在图中，线段 AD 还具有怎样的性质？为什么？由此你能得到什么结论？
可分解成下面三个方面来理解：
1. 等腰三角形的顶角的平分线，既是底边上的中线，又是底边上的高。
∵AB ＝ AC， ∠1 ＝∠2（已知）∴BD ＝ DC， AD⊥BC（等腰三角形三线合一）
2. 等腰三角形的底边上中线，既是底边上的高，又是顶角平分线。
∵AB ＝ AC BD ＝ DC （已知）∴AD⊥BC ∠1 ＝∠2 （等腰三角形三线合一）
3. 等腰三角形的底边上的高，既是底边上的中线，又是顶角平分线。
∵AB＝AC AD⊥BC （已知）∴BD＝DC ∠1＝∠2 （等腰三角形三线合一）
1.（1）已知等腰三角形的一个角为 40°，则其它两个角分别为 。
（2）已知等腰三角形的一个外角为 70°，则这个三角形的三个内角分别为 。
70° 、70°或40°、100°
110° 、35° 、35°
2. 如图，在△ABC 中，AB = AC，点 D 在 BC 上，且 BD = AD，DC = AC，求∠B 的度数.
解：∵AB = AC，∴∠B =∠C（等边对等角）.同理可得∠B =∠BAD，∠CDA =∠CAD.设∠B = x，则∠C =∠BAD = x，∴∠CAD =∠CDA = 2x.在△ADC 中，∠C +∠CDA +∠CAD =180°，即 x + 2x +2x = 180°，∴ x = 36°，即∠B =36°.
3. △ABC 中，AB ＝ AC，D 是 BC 边上的中点，DF⊥AC 于 F，DE ⊥ AB 于 E . 求证：D E＝ DF。
证明：连接 AD， ∵AB＝ AC，BD＝ DC（已知）∴AD 是∠BAC 的平分线.（等腰三角形三线合一）又∵DE⊥AB DF⊥AC，∴DE＝ DF（角平分线上的点到这个角的两边距离相等）.
4. 已知：如图，点 B，E，C，F 在同一条直线上，AB = DE，AC = DF，BE = CF. 求证：∠A =∠D.
证明： ∵BE＝ CF，∴BE + CE＝ CF + EC，∴BC = EF.又∵AB = DE AC = DF，∴△ABC ≌△DEF（SSS）.∴∠A =∠D.
5. 如图，在△ABC 中，AB = AC，点 D，E 都在边 BC 上，且 AD = AE，那么 BD 与 CE 相等吗？请证明你的结论.
解：∵AB = AC，∴∠B =∠C（等边对等角）.同理可得∠ADE =∠AED.∴∠ADB =∠AEC.∴△ABD ≌ △ACE（AAS）.∴BD = CE.