初中数学浙教版九年级上册3.5 圆周角课时练习

这是一份初中数学浙教版九年级上册3.5 圆周角课时练习，共7页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
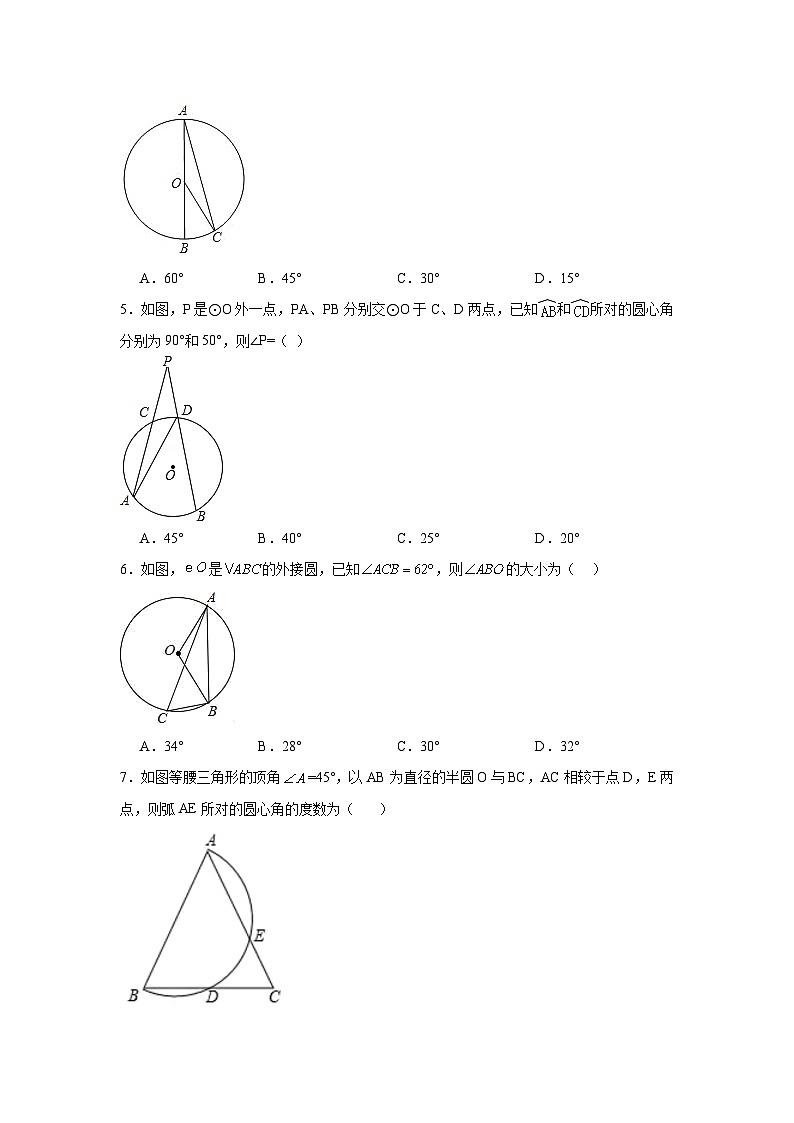
3.5圆周角随堂练习-浙教版数学九年级上册学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．如图所示，MN是⊙O的直径，作AB⊥MN，垂足为点D，连接AM，AN，点C为弧AN上一点，且弧AC=弧AM，连接CM，交AB于点E，交AN于点F，现给出以下结论：①AD=BD；②∠MAN=90°；③弧AM=弧BM；④∠ACM+∠ANM=∠MOB；⑤AE=MF，其中正确结论的个数是（　　）A．2 B．3 C．4 D．52．如图，是的弦，半径，为圆周上一点，若所对应圆心角的度数为，则的度数为（   ）  A． B． C． D．3．如图，A、B、C是圆O上的三点，已知，则的度数是（    ）A． B． C． D．4．如图，AB为⊙O的直径，点C在⊙O上，若∠C=15°，则∠BOC =（ ）A．60° B．45° C．30° D．15°5．如图，P是⊙O外一点，PA、PB分别交⊙O于C、D两点，已知和所对的圆心角分别为90°和50°，则∠P=（ ）A．45° B．40° C．25° D．20°6．如图，是的外接圆，已知，则的大小为（    ）A．34° B．28° C．30° D．32°7．如图等腰三角形的顶角=45°，以AB为直径的半圆O与BC，AC相较于点D，E两点，则弧AE所对的圆心角的度数为（      ）A．40° B．50°C．90° D．100°8．如图，AB为的直径，点C在上，弦CD与AB相交于点E，连接AD，OC，若，，则的度数为（    ）．A．63° B．72° C．84° D．86°9．如图：点A，B，C都在⊙O上，且点C在弦AB所对的优弧上，若∠AOB＝72°，则∠ACB的度数是（　　）A．18° B．30° C．36° D．72°10．如图，点在上，是的切线，为切点，的延长线交于点，，则的度数是（      ）A．22．5° B．20° C．30° D．45° 二、填空题11．如图，在中，，是斜边上的中线，为中点，若点在以为直径的圆周上，则      .12．如图，A、B、C是⊙O上的点，若∠BOC=100°，则∠BAC=       °．13．如图，是的直径，是弦，，则的度数为          ．14．如图，点、、在上，，连接并延长，交于点，连接，．若，则的大小为      °．15．如图，是的直径，是弦，，若且，则等于        16．如图，△ABC的顶点 A、B、C均在⊙O上，若∠ABC=26°，则∠AOC的大小是  ． 17．如图，△ABC的三个顶点都在⊙O上，AD是直径，且∠CAD＝62°，则∠B的度数为       .18．如图，AB是⊙O的直径，BC为⊙O的切线，∠ACB＝40°，点P在边BC上，则∠PAB的度数可能为          (写出一个符合条件的度数即可)19．如图，已知AB是⊙O的弦，C是的中点，连接OA，AC，如果∠OAB＝20°，那么∠CAB的度数是     ．20．如图，A、B、C是⊙O上的点，且∠ACB＝130°，在这个图中，画出下列度数的圆周角：30°，40°，50°，90°，其中仅用无刻度的直尺能画出的圆周角有       °． 三、解答题21．如图，AB是⊙O的直径，弦AD平分∠BAC，过点D分别作DE⊥AC、DF⊥AB，垂足分别为E、F，⊙O与AC交于点G．（1）求证：EG＝BF；（2）若⊙O的半径r＝3，BF＝1，求AG长．22．【探究发现】（1）如图①，的顶点在正方形两条对角线的交点处，，将绕点旋转，旋转过程中，的两边分别与正方形的边和交于点和点（点与点，不重合），则与之间满足的数量关系是________；【类比应用】（2）如图②，若将（1）中的“正方形”改为“的菱形”，其他条件不变，当时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由；【拓展延伸】（3）如图③，在四边形中，平分，，，过点作，交的延长线于点．若，，求的长．  23．如图，已知A，B，C均在⊙O上，请用无刻度的直尺作图．(1)如图1，若点D是的中点，试画出的平分线；(2)若，点D在弦上，在图2中画出一个含角的直角三角形．24．如图，A、P、B、C是⊙O上的四个点，∠APC=∠CPB=60°．（1）△ABC的形状是　　；（直接填空，不必说理）（2）延长BP到D点，使得BD=CP，连接AD，试判断∠ADP的形状，并说明理由．25．如图，在中，，，求的度数．