初中4 探索三角形相似的条件一等奖课件ppt

这是一份初中4 探索三角形相似的条件一等奖课件ppt，共28页。PPT课件主要包含了教学目标，复习回顾，∴△ADE∽△ABC等内容，欢迎下载使用。
1、知道判断两个三角形相似的两种方法。2、能利用相似三角形的定义及 判定定理1判定两个三角形的相似。
三角对应相等，三边对应成比例的两个三角形叫做相似三角形。
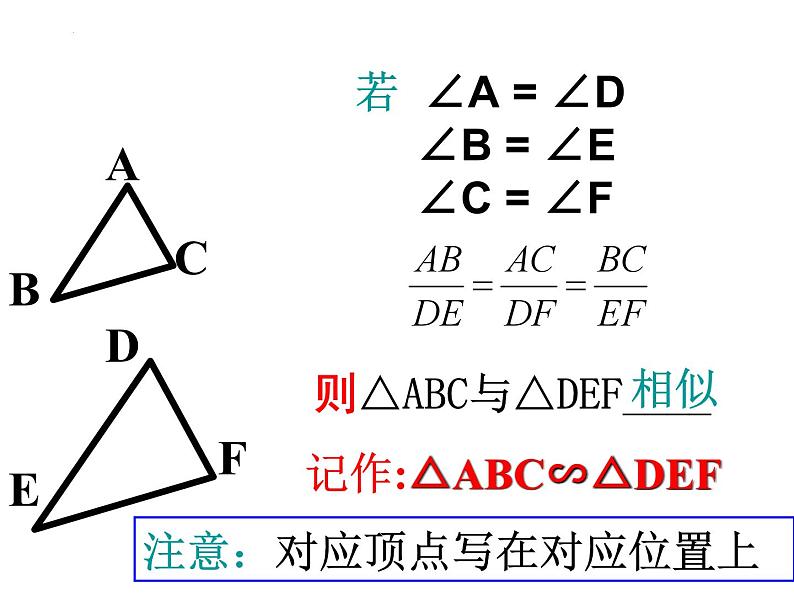
则△ABC与△DEF____
若 ∠A = ∠D ∠B = ∠E ∠C = ∠F
记作:△ABC∽△DEF
注意：对应顶点写在对应位置上
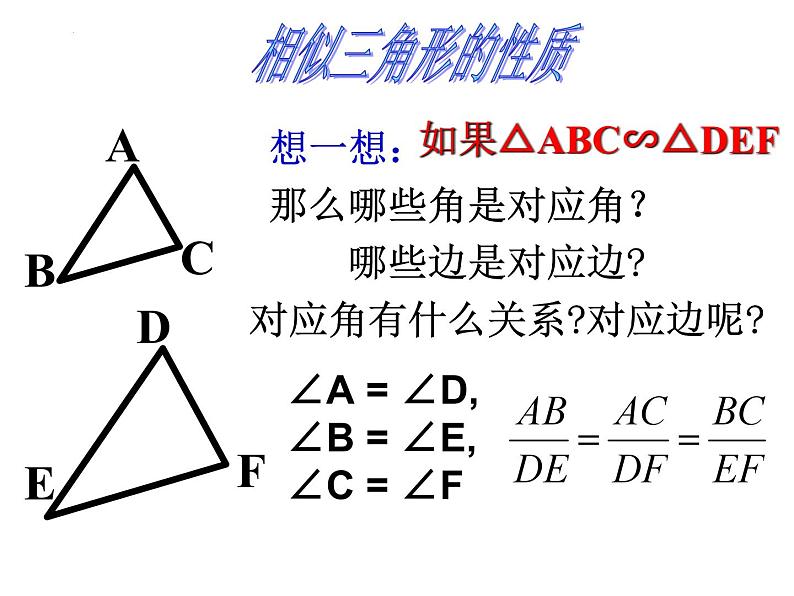
∠A = ∠D,∠B = ∠E,∠C = ∠F
想一想： 那么哪些角是对应角？ 哪些边是对应边?对应角有什么关系?对应边呢?
如果△ABC∽△DEF
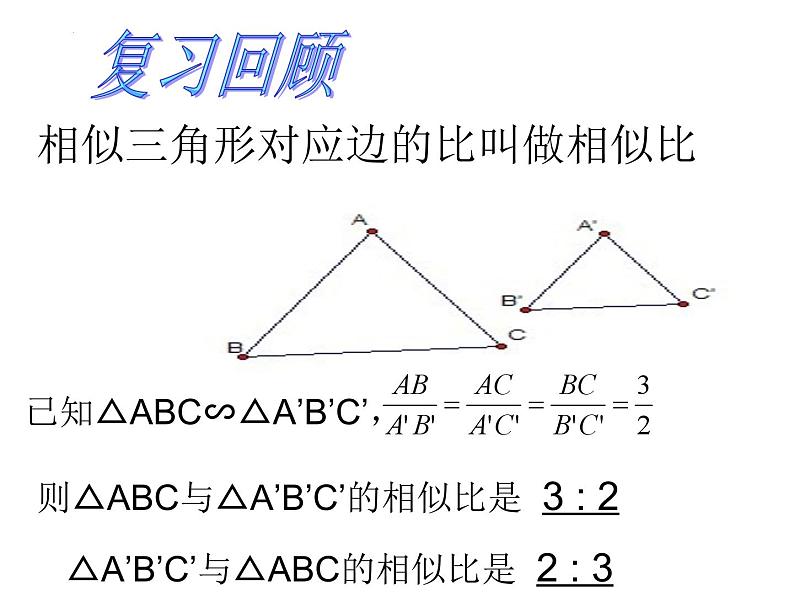
已知△ABC∽△A’B’C’，
相似三角形对应边的比叫做相似比
则△ABC与△A’B’C’的相似比是 3 : 2 △A’B’C’与△ABC的相似比是 2 : 3
学习新课：相似三角形判定定理
思考：两个三角形至少满足哪些条件就相似呢？能否类比两个三角形全等的条件，寻找判定两个三角形相似的条件呢？
想一想 如果两个三角形只有一个角相等，它们一定相似吗？如果有两个角分别相等呢？
由此得到判定两个三角形相似的定理1：两角分别相等的两个三角形相似.
几何语言： ∵ ∠A =∠D,∠B =∠E, ∴ △ ABC∽ △ DEF,
1.如图，△ABC∽△ADE，求x。
2.如图，△ABC∽△DEF ，求 y、m、n的值。
复习：平行线分线段成比例定理：两条直线被一组平行线所截，所得的对应线段成比例. l1∥l2∥l3.
平行于三角形一边的直线与其他两边相交，截其他两边(或两边的延长线），所得的对应线段成比例。
平行于三角形一边的直线和其他两边 （或两边的延长线）相交，所构成的三角形与三角形相似。
若DE∥BC，则△ADE∽△ABC
已知：如图,在△ABC 中,DE//BC, DE分别交AB,AC 于点D,E, 求证：△ADE∽△ABC
证明：在△ADE与△ABC中, ∠A=∠A, ∵DE//BC, ∴∠ADE=∠B, ∠AED=∠C.
过E作EF//AB,EF交BC于F点.
在平行四边形BFED中,DE=BF,DB=EF.
即:△ADE与△ABC中, ∠A=∠A,∠ADE=∠B, ∠AED=∠C.
故：∵ DE//BC, ∴△ADE∽△ABC
相似三角形判定的预备定理
若DE∥BC，△ADE∽△ABC
1．如图，DE∥BC，AD=8，DB=12， AC=15，DE=7，求AE和BC的长．
2、如图，在 ABCD中，E在BC上，BE:EC=3:2，连接AE、BD交于点F，则BE:AD=_____，BF:FD=_____。
3．如图，在□ABCD中，EF∥AB，DE:EA=2:3，EF=4，求CD的长．
4.如图，E在□ABCD的边BC的延长线上，连结AE交CD于F，图中共有相似三角形（ ） A1对 B2对 C3对 D4对
5、若 DE∥BC,DF∥AC，BF=3,CF=2,AD=1.5,DF=6,你能求出线段AE的长度吗？
∵DE∥BC,DF∥AC
∴四边形DFCE为平行四边形
∴FC=DE=2，EC=DF=6
∴AE=AC-CE=10-6=4